Utolsó módosítás: 2008. december 3.
Ez a feladatsor a második verseny első, december 4. csütörtök délutáni turnusához tartozik.
Le lehet tölteni az összes példa be- és kimenetet és példa forráskódot egyben: z3p.tgz vagy z3p.zip.
A feladatok nem nehézségi sorrendben vannak.
Egy elhanyagolt kert négyzet alakú, és N-szer N kis négyzet alakú mezőből áll. Minden mező vagy tiszta, vagy gyomos. Ha egy mező négy élszomszédja közül legalább kettő gyomos, akkor pár nap múlva ezt a mezőt is felveri a gyom. Ha egy mező egyszer gyomos, akkor sose lesz magától tiszta.
A program bemenetben megadja a kert kezdeti állapotát, és kiszámolja, hogy fog kinézni a kert elég sok idő múlva, amikor már a lehető legjobban elgyomosodott.
A program bemenetében az első sor az egyetlen N egész számot tartalmazza
(2 <= N < 35), ami a kert méretét adja meg.
A következő N sor az újsor jel előtt N karaktert tartalmaz,
mindegyik pont (.) ha a megfelelő mező tiszta,
vagy kukac (@) ha gyomos a kezdeti állapotban.
A program kimenete N sorból áll,
amelyek a kert gyomosságát írják le
a kialakuló egyensúlyi állapotban.
Itt egy példa. Ha a bemenet a következő,
15 @.............@ .....@......... ............... .@..@@@.@...... ............... ............... ...........@... .....@......... .@..@........@. ..........@.... ...@..........@ ..............@ .....@.....@... ...........@... ..@...@.....@..akkor a kimenet,
@.............@ ....@@@@@...... ....@@@@@...... .@..@@@@@...... ............... ............... ...........@... ....@@......... .@..@@.......@. ..........@.... ...@..........@ ..............@ .....@.....@@.. ...........@@.. ..@...@....@@..
Itt van még több be- és kimenet.
Ebben a feladatban ki kell válogatni egy zárthelyi eredménylistájából azokat a hallgatókat, akik az átlagos pontszámnál jobb zárthelyit írtak.
A program bemenetében néhány (legalább 2, legfeljebb 120) sor áll, mindegyik egy hallgatóhoz tartozik, aki egy bizonyos (képzeletbeli) zárthelyit megírt. Minden sorban először a hallgató által elért pontszám áll (egy 0 és 200 közötti egész szám), majd egy szóköz, majd a hallgató teljes neve (legfeljebb 40 karakter, állhat két vagy három szóból), majd egy újsor karakter.
A kimenetbe pontosan azon hallgatók nevét kell kiírni, akiknek a pontszáma magasabb, mint az összes megadott pontszám átlaga (számtani közepe). A hallgatók a kimenetben ugyanolyan sorrendben szerepeljenek, mint a bemenetben.
Itt egy rövid példa. A bemenet a következő.
148 Váradi Piroska 120 Szabó Annamária 192 Katona Csaba 31 Sándor Richárd 70 Pintér Györgyi 107 Váradi Dorottya 165 Szilágyi Erika 119 Hegedüs Bernadett
Ekkor az átlagos pontszám pontosan 119, ezért az ennél magasabb pontszámú hallgatókat kell kigyűjteni. A kimenet így a következő.
Váradi Piroska Szabó Annamária Katona Csaba Szilágyi Erika
Több példa is van.
Egységnyi ellenállásokból soros és párhuzamos kapcsolásokkal áramkört építettünk. A program az áramkör eredő ellenállását számítja ki.
(Megjegyzés: az 5. és 3. feladat könnyebb, mint ez, azt oldd először!)
A program bemenete egy sorból áll, ami az ellenállás kapcsolását határozza meg.
Ez egy prefix formájú kifejezés, ami az 1, s, p
karakterekből áll, amik rendre egy egységnyi ellenállást, soros,
illetve párhuzamos kapcsolást jelentenek.
(A képlet után újsor jel áll. A bemenet legfeljebb 120 karakter hosszú.)
Pontosabban a szabályok a következők.
Az 1 számjegy egy egységnyi ellenállásnak felel meg.
Ha X és Y két áramkör leírása,
akkor sXY és pXY rendre
ezek soros illetve párhuzamos kapcsolásának felel meg.
Ha az első áramkör ellenállása x, a másodiké y,
akkor soros kapcsolásuk eredő ellenállása x + y,
párhuzamos kapcsolásuké pedig 1/(1/x + 1/y).
A programnak pontosan ki kell számolnia a kapcsolás ellenállását,
és a kapott racionális szám egyszerűsített alakját kell kiírnia.
A kimenet a számláló decimális alakjából, egy per (/) jelből,
a nevező decimális alakjából, majd egy újsor jelből áll.
Ehhez minden részáramkör ellenállását számláló és nevező párjaként érdemes tárolni, ezeket minden művelet után egyszerűsített alakra kell hozni. Ha így számol, a bemenetek esetén hat számjegyűnél hosszabb számlálók vagy nevezők nem fordulnak elő.
Például ha a bemenet
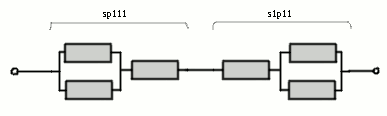
ssp111s1p11
akkor a következő áramkörről van szó,

ennek az eredő ellenállása 3, ezért a kimenet
3/1
Íme még pár példa.
Ebben a feladatban egy táblázatban fogja megkeresni a leghosszabb függőlegesen egymás alatt lévő teli mezőkből álló részt.
A program bemenetében az első sor egy N egész számot ad meg (1 <= N <= 300).
A maradék N sor mindegyikében N darab pont vagy kukac jel áll, majd egy újsor jel.
Ezek együtt egy N-szer N-es négyzetes táblázatot adnak meg,
aminek mindegyik mezője vagy teli, amit kukac (@) jelöl,
vagy kikapcsolt, amit pont (.) jelöl.
A program megkeresi a legmagasabb, hézag nélkül egymás alatti teli cellákból álló résztáblázatot a táblázatban. A program kimenete egyetlen egész szám, ennek a legmagasabb teli oszlopnak a hossza. (A kimenet végére újsor jelet kell írni.)
Például legyen a bemenet a következő.
15 @@@@@..@...@.@@ ...........@.@@ ...@@.@...@@@@@ @@.@..@..@.@..@ .....@.@..@...@ @@..@.....@..@@ @....@....@..@@ ..@@@@@.@..@@.. @..@@@@@@@..@.. .@.@@..@@@.@..@ @......@....@.@ .@.@@@.@@.@...@ .@@@.@@@..@@..@ ......@@..@@... .@.....@.@...@.
Ekkor a kimenet
7
Egy 7 magas oszlopot színnel kiemeltem, egy másik a táblázat jobb felső sarkából indul.
Még pár példa.
A program szavak egy listájáról kiszámítja, hogy az egyes szavak hány példányban szerepelnek a listában.
Ezt a programot ruby nyelven érdemes megírni. Ha elakadsz, esetleg olvasd el azt a pár sort, amit az asszociatív tömbökről írtam az s2f6 mintafeladatnál.
A program bemenete sok (legalább 1, legfeljebb 16000) sorból áll, minden sorban egy legfeljebb 15 betűs angol szó (és egy újsor jel) áll. A szavak között lehetnek megegyezőek.
A kimenetben a bemenet minden sorához egy sor tartozik, ugyanolyan sorrendben. Minden sorban csak egy egész szám van, ami azt mondja meg, hogy a megfelelő szó az egész bemenetben hányszor fordul elő. (Csak teljes szavas egyezések számítanak, az nem, amikor egy szó egy másik szó belsejében fordul elő.)
Például lehetne a bemenet a következő.
ebb ebb ebb type fast ebb fast type deflector ebb
Ekkor a kimenet ez legyen.
5 5 5 2 2 5 2 2 1 5
Az első három szám 5, mert az "ebb" szó ötször fordul elő. Utána kétszer a 2 szerepel, mert a "type" és a "fast" is még egyszer előjön. Satöbbi.
Itt a többi példa is.
Ebben a feladatban egy listából ki kell választania a két legkisebb számot.
A program bemenete egy sor, amiben pontosan tizennégy (14) szám áll szóközzel elválasztva. Mindegyik szám legfeljebb háromjegyű nemnegatív egész, és lehetnek köztük egyenlőek is.
A program kimenete két sorból áll, mindkét sorban egyetlen szám. Az első sorban a bemenetbeni számok közül a legkisebb áll, a második sorban a második legkisebb. A két kimenet lehet egyenlő is, ha a bemenetben a legkisebb szám kétszer fordul elő.
Például ha a bemenet
48 69 17 57 90 88 53 40 57 0 9 44 26 32
akkor a kimenet
0 9
viszont ha a bemenet
20 95 42 54 85 86 24 51 76 57 55 20 33 27
akkor a kimenet
20 20
mert a legkisebb és a második legkisebb szám is 20.
Ha kell, több példa is van itt.
Sok sikert a versenyhez!