1. zárthelyi

1. . Határozza meg értékét. Válaszát algebrai alakban adja meg. (2 pont)

2. Oldja meg az egyenletet. (4 pont)

3. Legyenek egy háromszög alapú gúla csúcsi: A (1;1;2), B(2,2;5), C(2;0;2) és D(1;3;3).

a.) Határozza meg a gúla térfogatát. (2 pont)

b.) Írja fel a B-n átmenő, az ACD lapra merőleges egyenes egyenletét. (4 pont)

c.) Határozza meg az AB és CD élek távolságát. (4 pont)

4. Határozza meg azt a legkisebb N természetes számot, melyre igaz, hogy minden esetén az sorozat elemeinek eltérése a sorozat határértékétől kisebb, mint (4 pont)

2. zárthelyi

1. Adott az függvény.

a.) Adja meg a függvény inverzét, az és értelmezési tartományát és értékkészletét.

b.) Számítsa ki ahatárértéket. (4 pont)

2. A derivált definíciója alapján döntse el, differenciálható-e az függvény az helyen. (3 pont)

3. Adja meg az alábbi függvények deriváltját (4 pont):

a.) b.)

4.Számítsa ki az alábbi függvény-, illetve sorozathatárértékeket:

a.), b,) 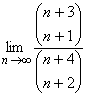(2+3 pont)

5. Adott az függvény. Határozza meg

a.) a függvény kritikus pontjait;

b.) azokat a nyílt intervallumokat, melyeken a függvény növekvő. (4 pont)

3. zárthelyi

1. Írja fel annak azoknak az egyeneseknek az egyenletét, melyek érintik az paraméteres egyenletrendszerű ellipszist és párhuzamosak a egyenletű egyenessel.. (4 pont)

2. Írja fel az függvény helyhez tartozó harmadfokú Taylor-polinomját.

(4 pont)

3. (4 pont)

4. 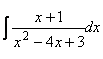(4 pont)

5. (4 pont)