GYAKORLÓ FELADATOK I.
I. éves építőmérnök és környezetmérnök
hallgatók számára
a Matematika B1 tantárgyhoz
1.
Adja meg a következő komplex számok trigonometrikus alakját:
![]() .
.
2.
Adja meg az algebrai alakot:
![]() .
.
3.
Számítsa ki és adja meg a választ algebrai alakban:
![]() ,
, ![]()
4.
Oldja meg az alábbi komplex egyenleteket:
a.)
![]() , b.)
, b.) ![]() , c.)
, c.) ![]() , d.)
, d.) ![]() ,
,
e.)
![]() , f.)
, f.) ![]() , g.)
, g.) ![]() .
.
5.
Egy szabályos háromszög két csúcsa a komplex számsíkon ![]() . Határozza meg a harmadik csúcs helyét.
. Határozza meg a harmadik csúcs helyét.
6.
Jelölje M: Magyarország lakóinak
halmazát,
F: a világ férfi lakóinak
halmazát,
A: a világ
analfabétáinak halmazát.
Fejezze
ki ezekkel azokat a halmazokat, melyek a következő személyeket tartalmazzák:
a.)
az összes külföldi analfabétát,
b.)
az összes analfabéta férfit,
c.)
a teljes férfi lakosságát és a magyar nőket,
d.)
az írástudó magyar férfiakat,
e.)
az írástudó magyar nőket,
f.)
a magyar analfabéta nőket és a külföldi írástudó férfiakat.
7. Tagadja a következő állításokat:
a.) „Minden f függvényre igaz, hogy ha ![]() , akkor
, akkor ![]() .”
.”
b.) „A BME-n van olyan tanszék, ahol nem
minden oktató osztályoz igazságosan.”
c.) „A BME-n nincs olyan tanszék, ahol
minden oktató igazságosan osztályoz.”
8. Bizonyítsa be teljes indukcióval, hogy
a.) ![]() , b.)
, b.) ![]() , ha
, ha ![]() .
.
9. Bizonyítsa be, hogy  .
.
10. Határozza meg az 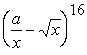 hatvány binomiális
tétel szerinti kifejtésének középső tagját.
hatvány binomiális
tétel szerinti kifejtésének középső tagját.
11. Számítsa ki az alábbi összegek pontos
értékét:
a.)  , b.)
, b.)  , c.)
, c.) ![]() (i: képzetes egység),
(i: képzetes egység),
d.) ![]()
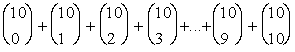 .
.
12. Mi az ![]() polinomnak a
polinomnak a ![]() polinommal való
osztásának maradéka?
polinommal való
osztásának maradéka?
a.)![]() ,
, ![]() ,
,
b) ![]() ,
, ![]() .
.
13. Írja fel a ![]() polinomot valós
együtthatós első és másodfokú polinomok szorzataként.
polinomot valós
együtthatós első és másodfokú polinomok szorzataként.
14. Legyen ![]() . Határozza meg azt a legkisebb N természetes számot, amelyre teljesül, hogy
. Határozza meg azt a legkisebb N természetes számot, amelyre teljesül, hogy ![]() esetén az
esetén az ![]() eltérése az
eltérése az ![]() sorozat határértékétől
kisebb, mint
sorozat határértékétől
kisebb, mint ![]() .
.
15. Írja fel az alábbi végtelen sorozatok
első néhány tagját. Vizsgálja meg, a sorozat korlátos-e, monoton-e,
konvergens-e. Határozza meg a konvergens sorozatok határértékét.
a.) ![]() , b.)
, b.) ![]() , c.)
, c.)
![]() .
.
16. Konvergensek-e az alábbi
számsorozatok? Ha igen, számítsa ki a határértéket:
a.)  , b.)
, b.)  , c.)
, c.) ![]() ,
,
d.) ![]() , e.)
, e.)  , f.)
, f.) 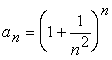 .
.
g.) ![]() , h.)
, h.) ![]() , i.)
, i.) 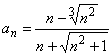 ,
,
j.) 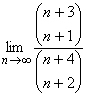 , k.)
, k.) ![]() , l.)
, l.)  .
.
17.* Egy egységnyi
oldalú szabályos háromszögbe írjunk egyenlősugarú köröket az ábrán látható
módon. Szaporítsuk az „emeletek” számát (n),
így mindig eggyel több körlapot helyezünk egy oldalra. Osszuk el a beírt
körlapok területének összegét a háromszög területével. Kérdés, hogy az így
kapott hányadosok sorozata konvergál-e, és ha igen, hová.

(n = 2)