GYAKORLÓ
FELADATOK II.
I. éves építõmérnökhallgatók számára
Matematika B1
1. Döntse el, hogy az alábbi függvények közül melyik páros, melyik páratlan és melyik nem tartozik egyik csoportba sem:
2. Ábrázolja az alábbi függvényeket:
,
.
3. Állapítsa meg az alábbi függvények értelmezési tartományát:
.
4. Adja meg a következõ függvények inverzét:
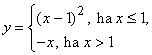
5. Képezze az alábbi függvények inverzét, állapítsa meg az inverzfüggvény értelmezési tartományát és értékkészletét:
,
6. Állapítsa meg az alábbi függvények értelmezési tartományát, értékkészletét és ábrázolja a függvényeket és inverzeiket:
,
.
7. Ábrázolja polárkoordinátarendszerben az alábbi függvényeket:
.
8. Ábrázolja az alábbi implicit módon ill. paraméteresen megadott görbéket:
a.) 
; 
; 
;
b.) 
; 
;
; 
.
15. Számítsa ki a következõ függvényhatárértékeket:
, 
, 
,
, 
, 
, 
, 
.
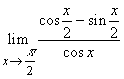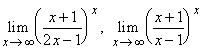16. Adja meg b értékét úgy, hogy az 
függvény folytonos
legyen az 
helyen.
17. Differenciálja a következõ függvényeket:
a.) 
, b.) 
, c.) 
,
d.) 
, e.) 
, f.) 
.
g.) 
, h.) 
.
18.
Meghatározandó az 
függvény grafikonját a 
pontban érintõ
egyenes egyenlete.
19. Az 
függvény görbéjének
mely pontjaiban vízszintes az érintõ?
20. Az 
függvény görbéjének
mely pontjaiban lesz az érintõnek az x
tengellyel bezárt szöge 45o?
21. Írja fel
azoknak az egyeneseknek az egyenletét, melyek érintik az 
függvény görbéjét és
átmennek a (0,-1) ponton!
22.
Meghatározandók az
függvény összes szélsõértékei a 
intervallumban.
23. Adja meg az 
abszolút maximumát és
abszolút minimumát a 
intervallumon.
24. Adott az 
függvény. Határozza meg c értékét a
(2;7) intervallumban úgy, hogy
legyen.
25. Döntse el, hogy a Rolle tétel
alkalmazható-e az 
függvényre a 
intervallumon. Ha igen, keresse meg c értékét (értékeit) a megadott
intervallumban úgy, hogy 
. Ha a tétel nem alkalmazható, magyarázza meg, miért nem.
26. Keresse meg azokat a
nyílt intervallumokat, melyeken az 
függvény
a.) monoton növő;
b.) monoton csökkenő;
c.) konkáv;
d.) konvex.
27. Keresse meg az f(x)
függvény inflexiós pontjait:
a.) 
, b.)
.
28. Számítsa ki az alábbi függvényhatárértékeket:
a.) 
, b.) 
, c.) 
, d.) 
,
e.) 
, f.) 
.
29. Vizsgálja és ábrázolja a következő függvényeket:
a.) 
, b.) 
, c.) 
, d.) 
,
e.) 
, f.) 
, g.) 
, h.) 
.