2. Feladat
Forgassa meg az x^2 + y^2 - 6x + 5 = 0, z = 0 görbét az y tengely körül. Számítsa ki a (2, 3^(1/2), 0) pontbeli paramétervonalak hajlásszögét, és írja fel az érintősík egyenletét ebben a pontban!
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()
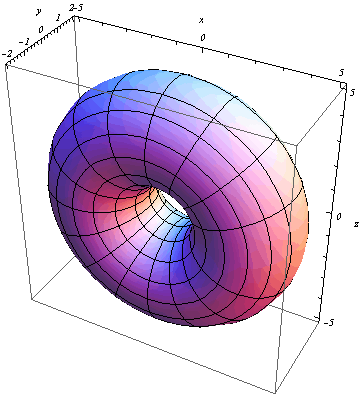
A grafikonon is látszik és behelyettesítéssel is ellenőriztem, hogy a pont rajta van a felületen.
![]()
![]()
A kört egységnyi sugarúnak véve és a középpontját origóba helyezve a kiválasztott pont értékei (-1/2, 3^(1/2)/2, 0) lennének, ami paraméterezésnél:
u = 2*Pi/3 és v = 0 -át jelent.
Paramétervonalak:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
A megoldásból látszik, hogy a két vektor által közrezárt szög, amely megegyezik a paramétervonalak pontbeli hajlásszögével, az 90[°].
Ilyen általános paraméterezés esetén a tórusz bármely pontjában a paramétervonalak hajlásszöge 90[°].
Az érintősík egyenletének számítása:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Ez az utolsó egyenlet az érintősík olyan legegyszerűbb alakja, ahol a bal oldali tag (D, a sík paramétere.) az origótól való távolságot mutatja.