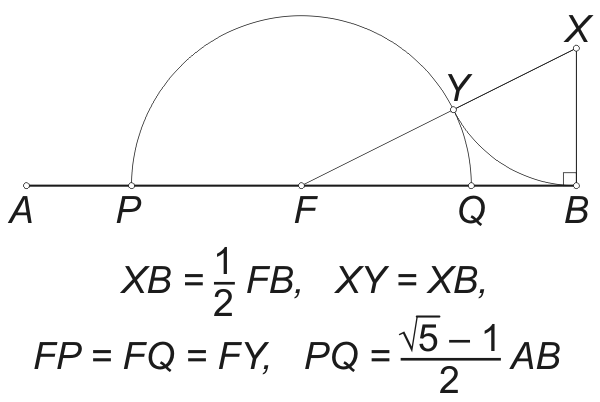ÁBRÁZOLÓ GEOMETRIA
R0 rajz 2018/19/2
Adott az ABCDAxBxCxDx parallelepipedon (parallelogramma alapú ferdehasáb) ABCD alaplapjának A, B és D csúcsa, továbbá az AAx oldalél Ax végpontja. Rajzoljuk meg a test ABCD lapjának az AB éllel párhuzamos középvonalát. Vegyük föl a többi lapnak is egy-egy középvonalát úgy, hogy a szomszédos lapok középvonalai kitérők legyenek (ekkor persze a szemközti lapokra rajzolt középvonalak párhuzamosak). Kicsinyítsük le az így kapott középvonalakat felezőpontjukból az aranymetszés (√5 – 1)/2 arányban. Egy szakaszra vonatkozó (számolással könnyen igazolható) szerkesztés az ábrán látható. Ábrázoljuk azt a konvex testet, amelynek 12 csúcsát a 6 kicsinyített középvonal végpontjai alkotják. Tüntessük föl a láthatóságot. A(70, 80, 150); B(90, 20, 180); D(130, 110, 170); Ax(40, 100, 210).
Bizonyítható, hogy az adott koordinátákkal meghatározott parallelepipedon kocka. Emiatt a fenti módon származtatott konvex test (szabályos) ikozaéder lesz. E test felületét 20 darab szabályos háromszög alkotja, úgy hogy minden csúcsban 5 lap találkozik. Éleinek száma 30. Az ikozaéder éleinek megrajzolásához vegyük észre, hogy a 6 kicsinyített középvonal mindegyike a befoglaló ABCDAxBxCxDx kocka egy-egy lapjára illeszkedő ikozaéderél. A hiányzó 24 ikozaéderélet pedig például úgy kaphatjuk meg, hogy a 12 ikozaédercsúcs mindegyikét összekötjük a hozzá legközelebbi (őt nem tartalmazó) kockalapon lévő két ikozaédercsúccsal. A megoldás könnyebb elképzelése érdekében javasoljuk a befoglaló kocka papírmodelljének elkészítését, lapjaira rárajzolva a kicsinyített középvonalakat.