ÁBRÁZOLÓ GEOMETRIA
R2 rajz 2018/19/2

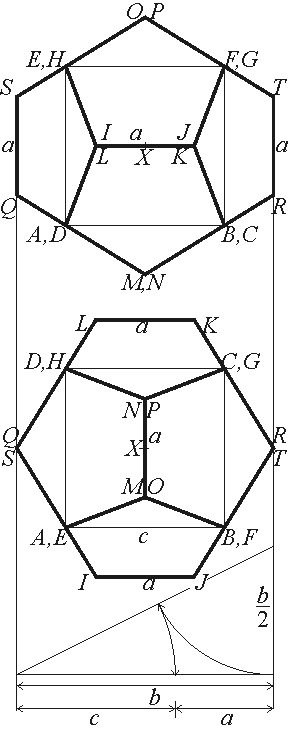
Adott az ABCDEFGH kockára épített szabályos dodekaéder (az ábra szerint), amelynek szemközti élei b távolságra vannak egymástól. Adott továbbá az XY szakasz, amelynek X végpontja a dodekaéder és a kocka közös középpontja. Az XY szakaszt vetítősugárrá transzformálva szerkesszük meg a dodekaéder XY irányából látható merőleges vetületét. A III. képsík a II. képsíkra legyen merőleges. A láthatóságot az I-II és a III-IV képsíkrendszerben is tüntessük föl. X(55, 130, 230); Y(95, 175, 277); b = 68. A kocka c és a dodekaéder a élhossza a b szakasz aranymetszéssel történő felosztásából származik az ábra szerint. Ez azt jelenti, hogy b : c = c : a = (1 + sqrt5) / 2 = 1.618... (Ebből jó közelítéssel a = 26, c = 42 adódik.) A képsík-transzformációk során az x12, x23, x34 tengelyek rendre az alábbi pontokon haladjanak át: X12(0, 180);  X23(175, 277);  X34(200, 115).