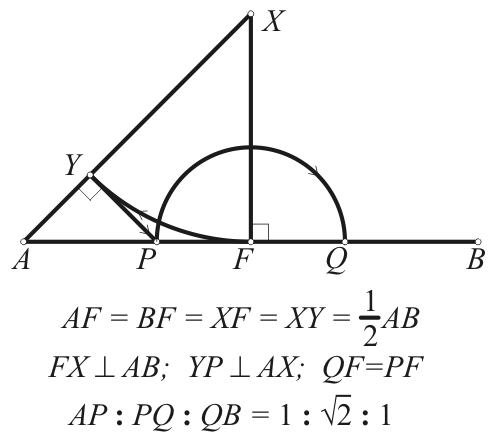ÁBRÁZOLÓ GEOMETRIA
R0 rajz 2020/21/1

Adott az ABCDA_xB_xC_xD_x parallelepipedon (parallelogramma alapú ferdehasáb) ABCD alaplapjának A, B és D csúcsa, továbbá az AA_x oldalél A_x végpontja. Osszuk fel a test minden élét 1 : √2 : 1 arányban három részre. Az osztópontok szerkesztése az alábbi ábrán látható. A test minden csúcsát csonkoljuk a belőle kiinduló élek csúcshoz közelebbi osztópontján áthaladó síkkal. Ábrázoljuk az így keletkező testet, és tüntessük fel a láthatóságot. A(70, 100, 165); B(90, 40, 195); D(130, 130, 185); A_x(40, 120, 225).

Bizonyítható, hogy az adott koordinátákkal meghatározott parallelepipedon egy kocka. Emiatt a fenti módon származtatott test egy félig szabályos archimedeszi poliéder az ún. csonkolt kocka lesz. Ennek felületét egybevágó szabályos nyolcszögek és szabályos háromszögek alkotják úgy, hogy minden csúcsban 2 nyolcszög és 1 háromszög illeszkedik egymáshoz. Ennek alapján a test matematikai jele (8, 8, 3). Javasoljuk a test modelljének elkészítését is.