Descriptive Geometry
Assignment A3 2020/21/1

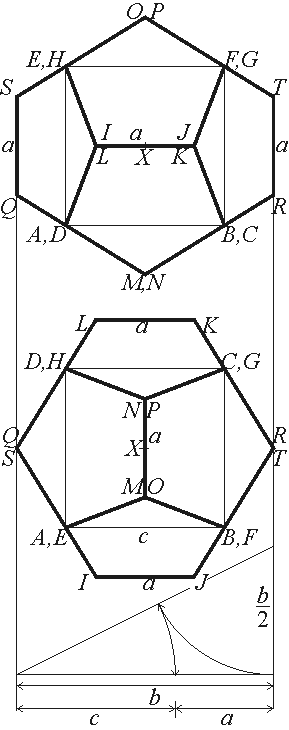
Given a dodecahedron derived from the cube ABCDEFGH as the figure shows. A line XY is also given; X is the common centre of the cube and the dodecahedron. Transforming XY into a projecting line, construct the image of the dodecahedron in the direction of XY. The 3^rd projection plane must be perpendicular to the 2^nd one. Show the visibility in system 1-2 and in system 3-4 of planes of projection. X(55, 130, 230);  Y(95, 175, 277);  b = 68. The edge length c of the cube and the edge length a of the dodecahedron are given by dividing b according to the golden ratio: b : c = c : a = (1 + sqrt5) / 2 = 1.618. The construction can be seen on the bottom of the figure. (Approaching  c = 42,  a = 26). The axes  x12, x23 and x34 are to be passed through the points  X12(0, 180),  X23(175, 277)  and  X34(200, 115), respectively.