LP feladatok megoldása az Excel Solver segítségével

Permission is granted to copy, distribute and/or modify this document

under the terms of the GNU Free Documentation License, Version 1.3

or any later version published by the Free Software Foundation;

    with the Invariant Sections being title and author, no Front-Cover Texts, and no Back-Cover Texts.

A copy of the license is included in the section entitled "GNU

Free Documentation License".

LP feladatok megoldása az Excel Solver segítségével

Szerző: Mádi-Nagy Gergely (BME Diff.egyenletek Tsz., ELTE TTK Operációkutatási Tsz.)

Tekintsük az alábbi LP feladatot (Prékopa: Lineáris Programozás I. 147. o.):

	x1	+2	x2	-4	x3	-	x4	≥	1
	x1	-	x2	+3	x3	+2	x4	≤	2
2	x1	-3	x2	+5	x3	-	x4	=	3

	x1	,	x2	,	x3	,	x4	≥	0

max (2	x1	+	x2	+2	x3	-2	x4	)

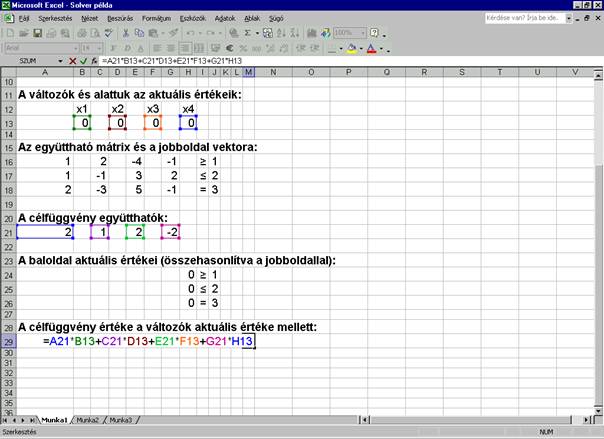
A könnyebb áttekinthetőség kedvéért magát a példát is beraktam az Excel táblába, bár ez a megoldáshoz nem szükséges:

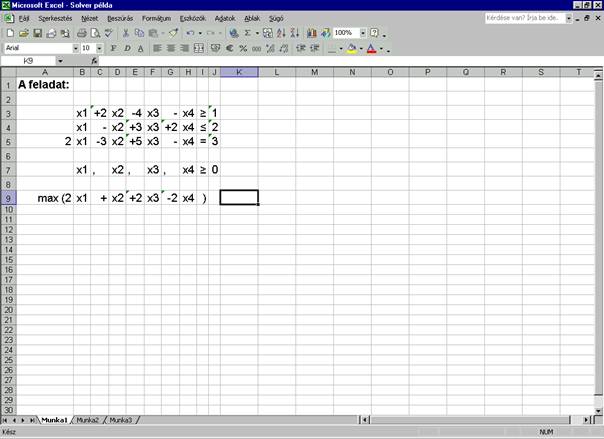
Ezután a változók értékeit tartalmazó cellák helyét adom meg, mely esetünkben $B$13;$D$13;$F$13;$H$13 lesz. Ezen cellák értékeit változtatja majd meg a solver a megoldás során. Adhatunk kezdőértékeket is (pl. 0-kat), ez nem befolyásolja a megoldás menetét, viszont javítja az áttekinthetőséget.

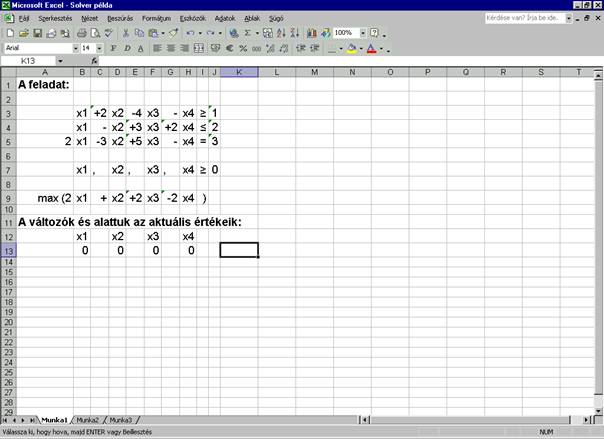
Az együtthatókat kiszedem, és struktúráltan beillesztem a táblába:

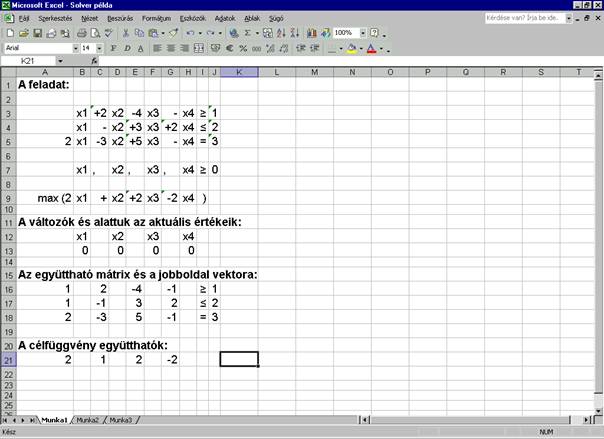
Kiszámolom a korlátozó feltételek baloldalának értékét az adott változóértékek mellett. Esetünkben ezek a $H$24, $H$25, $H$26 cellákba kerültek. Az alábbi képen a $H$24 értékének képlete jól mutatja az eljárást:

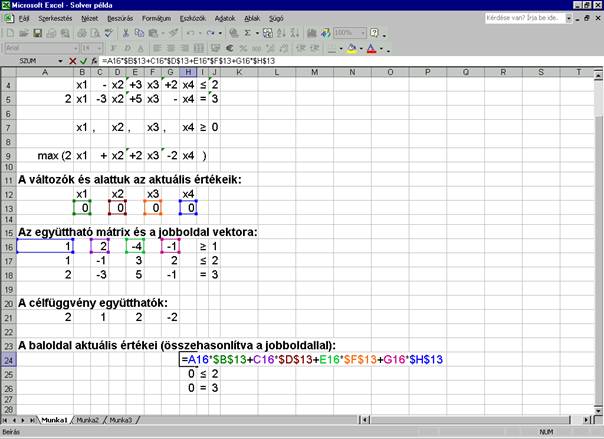
A célfüggvény értékét hasonló módon egy adott cellában kiszámítjuk ($M$29):

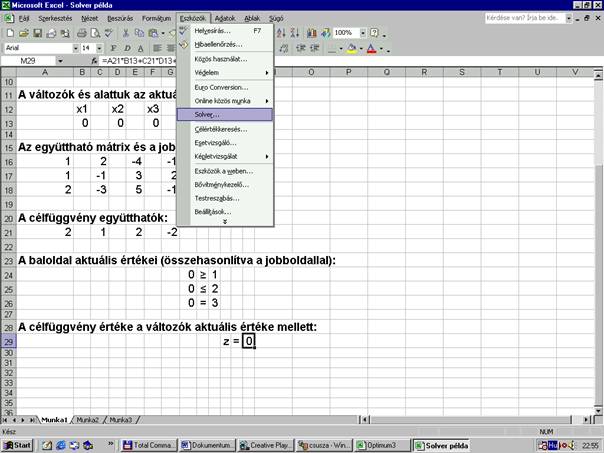
Az „Eszközök” menüben rákattintunk a Solverre. Ha nem találjuk, akkor valószínű nincs feltelepítve, ekkor a függelékben szereplő telepítési útmutatás szerint járjunk el.

Az alábbi ablakot kapjuk:

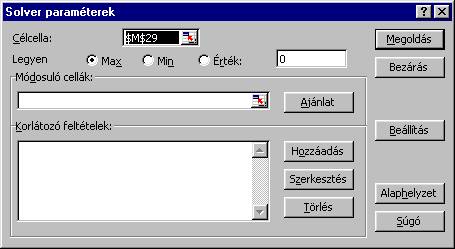
A célcella, és a célfüggvény jellege (max) itt már helyesen van kitöltve. A módosuló celláknál a változók celláira kell hivatkozni:

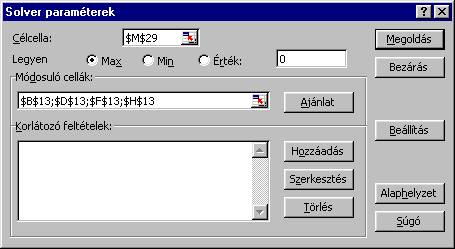
A korlátozó feltételek hozzáadásánál meg kell jelölni a feltétel baloldalának illetve jobboldalának megfelelő cellát, illetve a két oldal közti relációt, például:

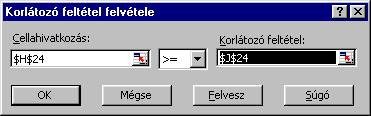
A feltételek bevitele után ezt látjuk:

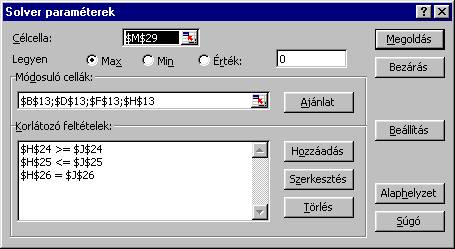
Mielőtt a feladatot megoldanánk, a „Beállítás” segítségével, egyrészt

· egyszerű módon megadhatjuk a változókra vonatkozó nemnegatívitási feltételeket („Nemnegatív feltételezése”),

· másrészt beállíthatjuk, hogy a Solver a feladatot szimplex módszerrel oldja meg („Lineáris modell feltételezése”). Megjegyezzük, hogy ezek után az alsó részben található nemlineáris eszközök (közelítés, differenciák, keresés) beállításai már nem mérvadóak.

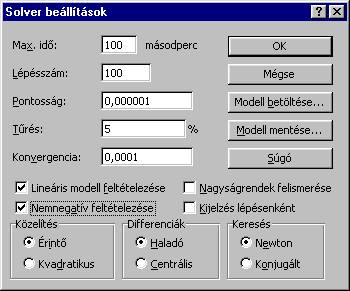
Ezek után megnyomhatjuk a „Megoldás” gombot (a Solver paraméterek ablakban).

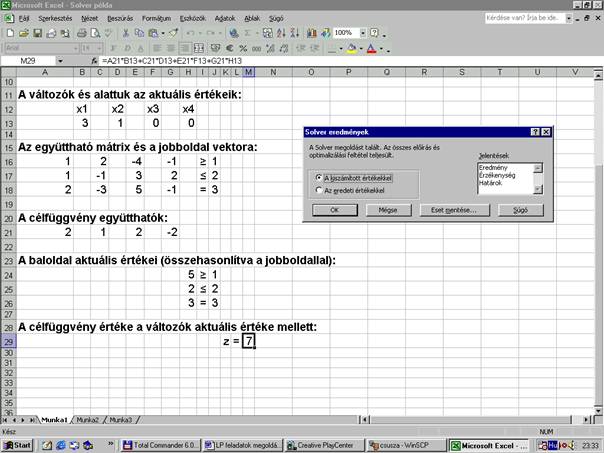
Látható, hogy a munkalapon a megfelelő cellákban máris az optimális megoldáshoz tartozó értékek jelentek meg. Ha a megoldás részletesebb elemzésére is kiváncsiak vagyunk, akkor a „Solver eredmények” ablakban jelöljük be a számunkra érdekes témák jelentéseit. Esetünkben az összes lehetőséget bejelöltem:

Az „OK” gomb megnyomása után a Solver három munkalapot generál. Az eredményjelentés az alábbi adatokat mutatja:

Microsoft Excel 10.0 Eredmény jelentés
Munkalap: [Solver példa.xls]Munka1
Készült: 2004.09.22. 23:33:58


Célcella (Max)
	Cella	Név	Eredeti érték	Végérték
	$M$29	=	0	7


Módosuló cellák
	Cella	Név	Eredeti érték	Végérték
	$B$13	x1	0	3
	$D$13	x2	0	1
	$F$13	x3	0	0
	$H$13	x4	0	0


Korlátozó feltételek
	Cella	Név	Cellaérték	Képlet	Status	Eltérés
	$H$24	x4	5	$H$24>=$J$24	Bőven	4
	$H$25	x4	2	$H$25<=$J$25	Éppen	0
	$H$26	x4	3	$H$26=$J$26	Bőven	0

Megjegyzést csak a „Korlátozó feltételek” „Status” és „Eltérés” sorai érdemelnek. Az „Eltérés” az optimális megoldáshoz tartozó baloldal és a jobboldal közti eltérés(változó) értékét mutatja. A „Status” egyenlőtlenségek esetén akkor „Éppen”, ha a baloldal eléri a jobboldalt, tehát ha az adott korlátozó feltétel határán vagyunk. Egyéb esetekben a „Status” „Bőven”.

Tekintsük az „Érzékenységjelentés” munkalapot:

Microsoft Excel 10.0 Érzékenység jelentés
Munkalap: [Solver példa.xls]Munka1
Készült: 2004.09.22. 23:33:58


Módosuló cellák
				Redukált	Objective	Megengedhető	Megengedhető
	Cella	Név	Végérték	költség	Célegyüttható	növekedés	csökkenés
	$B$13	x1	3	0	2	1E+30	1,75
	$D$13	x2	1	0	1	1E+30	4
	$F$13	x3	0	-7	2	7	1E+30
	$H$13	x4	0	-21	-2	21	1E+30

Korlátozó feltételek
				Shadow	Feltétel	Megengedhető	Megengedhető
	Cella	Név	Végérték	Árnyékár	jobb oldala	növekedés	csökkenés
	$H$24	x4	5	0	1	4	1E+30
	$H$25	x4	2	8	2	1E+30	0,5
	$H$26	x4	3	-3	3	1	1E+30

A „Módosuló cellák” táblázatból a „Redukált költség” a szimplex tábla alsó (c-z) sorának értékeire utal. A „Megengedhető növekedés/csökkenés” a megfelelő célfüggvény együttható változatásainak azon határait adja meg, melyen belül a feladat optimális megoldása nem változik (persze a célfüggvény értéke igen).

A „Korlátozó feltételek” táblázatban a „Név”-hez került x4 értékek helytelenek, itt az Excel csak megpróbált a korlátozó feltételeknek valamilyen cimkét adni. Az „Árnyékár” a duál feladat megoldását mutatja. A „Megengedhető növekedés/csökkenés” a megfelelő feltétel jobboldala változatásainak azon határait adja meg, melyen belül a feladat optimális megoldáshoz tartozó bázisa nem változik (persze a bázisváltozók értékei értékei igen). Ez a táblázat úgyis értelmezhető, hogy a duál feladatra adja meg ugynazaokat az értékeket, mint a „Módosuló cellák” a primálra. A különbség csak az első két oszlop jelentésében van, nevezetesen a duálmegoldás a második oszlopban van, míg a duál feladat redukált költségeit a harmadik és első oszlop különbségeként kaphatjuk meg.

Végül nézzük a „Határok jelentés”-t:

Microsoft Excel 10.0 Határok jelentés
Munkalap: [Solver példa.xls]Határok jelentés 1
Készült: 2004.09.22. 23:33:58


		Cél
	Cella	Név	Végérték
	$M$29	=	7


		Módosuló		Alsó	Cél	Felső	Cél
	Cella	Név	Végérték	határ	eredmény	határ	eredmény
	$B$13	x1	3	3	7	3	7
	$D$13	x2	1	1	7	1	7
	$F$13	x3	0	0	7	0	7
	$H$13	x4	0	0	7	0	7

Ez esetben az „Alsó/Felső határ” és a megfelelő „Cél(függvény) eredmény” a következőkre utal. Az adott optimális megoldásból kiindulva, egy-egy változót milyen határok közt tudunk mozgatni úgy, hogy a korlátozó feltételek továbbra is teljesüljenek, és a határokon felvett változóértékek mellet mekkora a célfüggvény értéke. Mivel ebben az esetben az egyik feltétel egyenlet, és itt mindkét bázisváltozó együtthatója nem nulla, így bármelyik változó értéket megváltoztatva ez a feltétel már nem teljesülne. Emiatt a változókra kapott alsó és felső határok egybeesnek. Más esetekben lehetőség van az egyes változók mozgatására, lásd a honlapon lévő többi solveres elemzést.

Jó munkát!

Mádi-Nagy Gergely

Függelék a Solver telepítéséhez

Szokásos telepítés esetén az Excel nem rakja fel a Solvert a számítógépünkre, ezért szükség lehet ennek a pótlólagos hozzáadására. Ekkor a teendőink a következők.

Rakjuk be az Office telepítőlemezt, majd índítsuk el a Setup programot (ha ez automatikusan nem történne meg). A megjelenő ablakban

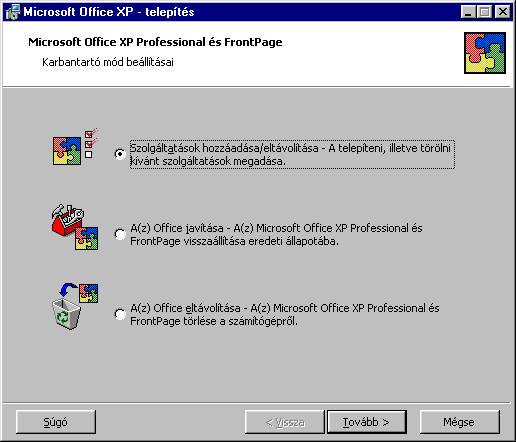
válasszuk a „Szolgáltatások telepítése/eltávolítása” pontot, majd menjünk tovább. Itt a „Solver” mellet levő ikont állítsuk a „Sajátgépről fut” vagy „Minden sajátgépről fut” állapotra:

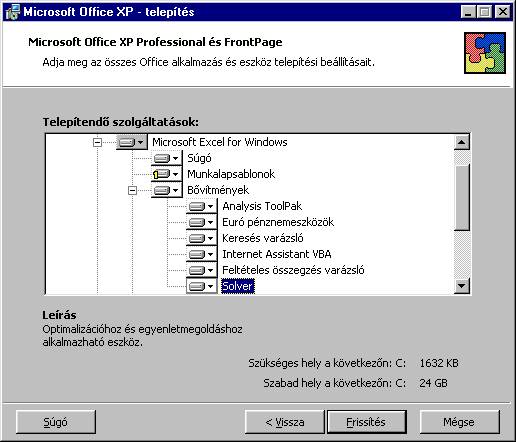
Majd a „Közös Office szolgáltatások”-on belül aktivizáljuk a a „Visual Basic for Applications” szolgáltatást is:

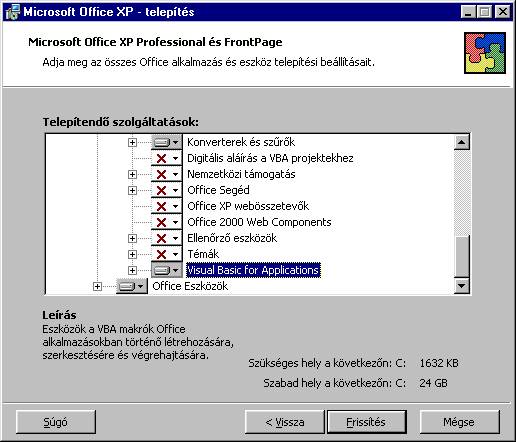
Ezután a „Frissítés” gomb megnyomásával befejezhetjük a telepítést.