Copyright (C) 2009 Gergely Mádi-Nagy.
Permission is granted to copy, distribute
and/or modify this document
under the terms of the GNU Free Documentation
License, Version 1.3
or any later version published by the Free Software Foundation;
with the Invariant Sections being title and author, no Front-Cover Texts, and no Back-Cover Texts.
A copy of the license is included in the
section entitled "GNU
Free Documentation License".
NLP feladatok megoldása az Excel Solver
segítségével
Szerző: Mádi-Nagy Gergely (BME Diff.egyenletek Tsz., ELTE TTK Operációkutatási Tsz.)
Az Excel Solver a
nemlineáris programozási feladatok megoldására általánosított redukált gradiens módszert (GRG) használ. Ennek
részletes technikai leírása megtalálható az alábbiakban:
L.S.
Lasdon, A. Waren, A. Jain and M. Ratner. Design and Testing of a Generalized
Reduced Gradient Code for Nonlinear Programming. ACM Transactions on Mathematical
Software 4:1 (1978), pp.
34-50.
L.S.
Lasdon and S. Smith. Solving Sparse Nonlinear Programs Using GRG. ORSA Journal on Computing 4:1 (1992), pp. 2-15.
Forrás:
http://www.solver.com
A
megoldás pontos menetéhez tekintsük az alábbi, kvadratikus programozási
feladatot. Forrás: http://www.cs.elte.hu/~margo/jegyzet/opkut/progmat-opkut-pdf.pdf
(5.1.1 feladat).
x2+3xy+y2-2xz-4yz+x-3y
-> min
x+y+z ≤ 10
2x-y ≥ 0
x, y, z ≥ 0
A
könnyebb áttekinthetőség kedvéért magát a példát is beraktam az Excel
táblába, bár ez a megoldáshoz nem szükséges:
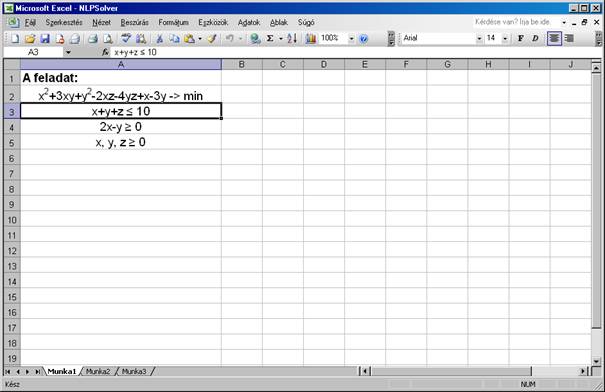
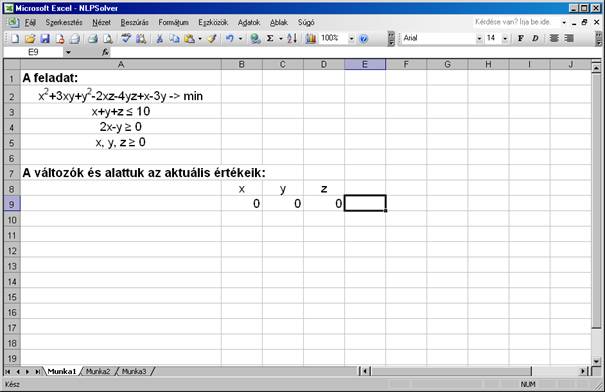
Ezután
a változók értékeit tartalmazó cellák helyét adom meg, mely esetünkben
$B$9;$C$9;$D$9 lesz. Ezen cellák értékeit
változtatja majd meg a solver a megoldás során. Adhatunk kezdőértékeket
is (pl. 0-kat), ez nem befolyásolja a megoldás menetét, viszont javítja az
áttekinthetőséget.
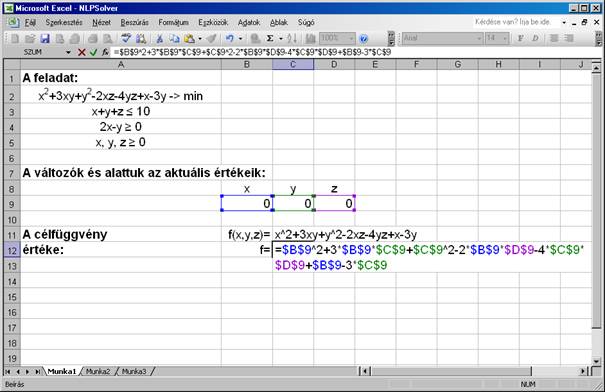
A
$C$12 cellába kerül a célfüggvény értéke, melyet a $B$9;$C$9;$D$9 cellákban
szereplő változó értékek függvényeként írtunk fel (a $C$11 képlet
szerint):
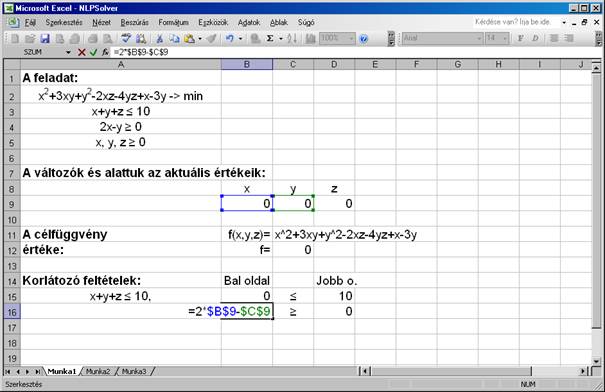
Hasonló módon a $B$15 ill.
$B$16 cellákba beírom az első illetve a második korlátozó feltétel
baloldalát a $B$9;$C$9;$D$9 cellákban szereplő változó értékek
függvényeként. Az alábbi ábrán épp a második feltétel képlete látszik:
Az
„Eszközök” menüben rákattintunk a Solverre. Ha nem találjuk, akkor
valószínű nincs feltelepítve, ekkor a függelékben szereplő telepítési
útmutatás szerint járjunk el.
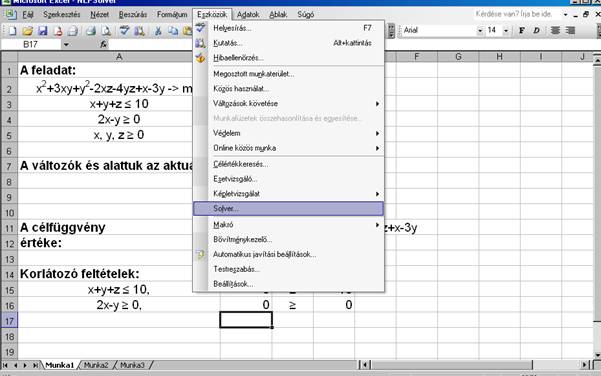
Az
alábbi ablakot kapjuk:
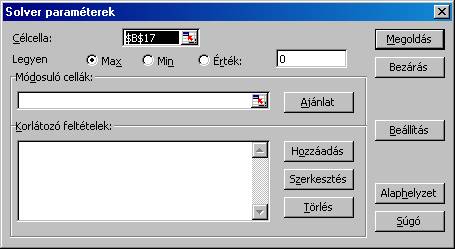
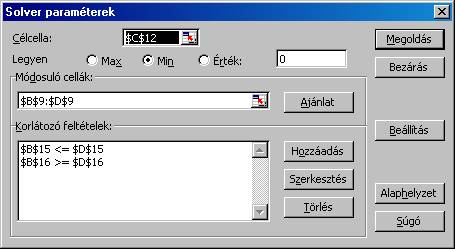
A célcellának beállítjuk a
célfüggvény értékét megadó $C$12 cellát. A feladat típusát átállítjuk Min-re. A
Módosuló cellák a változók értékeit tartalmazó $B$9;$C$9;$D$9 cellák lesznek:
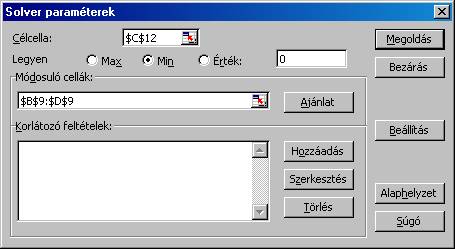
A
korlátozó feltételek hozzáadásánál meg kell jelölni a feltétel baloldalának
illetve jobboldalának megfelelő cellát, illetve a két oldal közti
relációt. Az első feltétel:
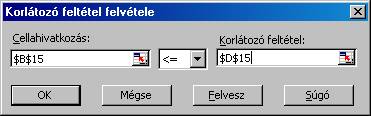
A második feltétel:
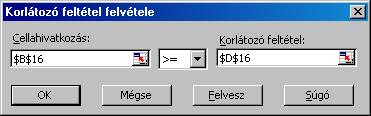
A
feltételek bevitele után ezt látjuk:
Mielőtt a feladatot
megoldanánk, a „Beállítás” segítségével válasszuk ki a számunkra
legmegfelelőbb megoldó algoritmust. A „Beállítás” gomb megnyomásával az
alábbi ablakot kapjuk:
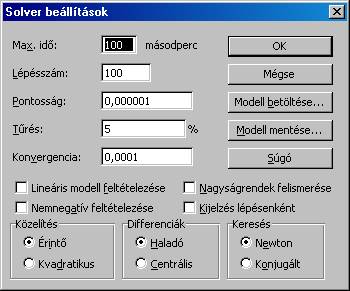
A feladat harmadik korlátozó
feltétele miatt a nemnegativitást majd fel kell tennünk, de bővebb
magyarázatot inkább a GCG (általánosított redukált gradiens) módszer
paraméterei kívánnak.
Közelítés:
Az iránymenti keresés során a
bázisváltozók értékeinek becslése.
·
Érintő: az
értéket az érintő lineáris függvényeként írjuk fel
·
Kvadratikus:
az értéket kvadratikusan extrapoláljuk.
Differenciák:
A parciális deriváltak
osztott differenciákkal való közelítése.
·
Haladó: ezt
használjuk, ha a korlátozó feltételek függvényértékei nem változnak túl
gyorsan. Általában ez a helyzet.
·
Centrális:
akkor van rá szükség, ha a korlátozó feltételek függvényei túl gyorsan változnak.
Bár több számolást igényel, de segíthet azokban az esetekben, amikor a Solver
azt üzeni, hogy nem tud tovább javítani a megoldáson.
Keresés:
A keresési irányt meghatározó
módszer kiválasztása.
·
Newton: kvázi-Newton
módszert használ, mely általában több memóriát, de kevesebb lépésszámot
igények, mint a konjugált gradiens módszer.
·
Konjugált: konjugált
gradiens módszert használ, mely kevesebbb memóriát használ, de általában több
lépésre van szüksége egy adott pontosság eléréséhez. Ajánlott pl. nagyobb
problémák esetén, ahol számít a felhasznált memória.
Ennek megfelelően mi az
alábbi beállításokkal dolgozunk:
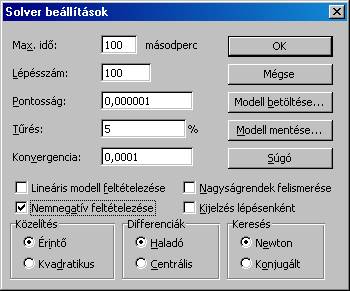
Ezek
után megnyomhatjuk a „Megoldás” gombot (a Solver paraméterek ablakban).
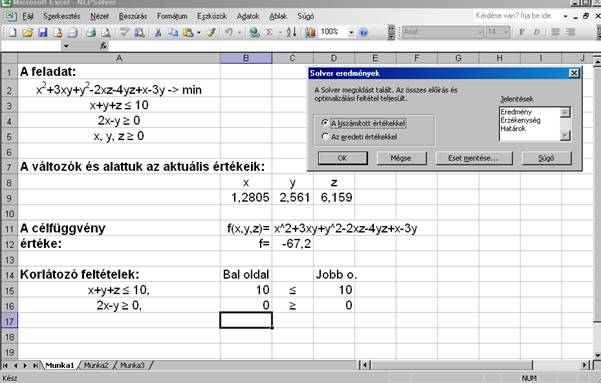
Látható,
hogy a munkalapon a megfelelő cellákban máris az optimális megoldáshoz
tartozó értékek jelentek meg. Ha a megoldás részletesebb elemzésére is
kíváncsiak vagyunk, akkor a „Solver eredmények” ablakban jelöljük be a
számunkra érdekes témák jelentéseit. Esetünkben az összes lehetőséget
bejelöltem:
Az
„OK” gomb megnyomása után a Solver három munkalapot generál. Az
eredményjelentés az alábbi adatokat mutatja:
|
Microsoft
Excel 11.0 Eredmény jelentés |
|
|
|
|||
|
Munkalap:
[NLPSolver.xls]Munka1 |
|
|
|
|
||
|
Készült:
2009.01.09. 11:07:49 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Célcella
(Min) |
|
|
|
|
||
|
|
Cella |
Név |
Eredeti
érték |
Végérték |
|
|
|
|
$C$12 |
f=
x^2+3xy+y^2-2xz-4yz+x-3y |
0 |
-67,22560976 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Módosuló
cellák |
|
|
|
|
||
|
|
Cella |
Név |
Eredeti
érték |
Végérték |
|
|
|
|
$B$9 |
x |
0 |
1,280487802 |
|
|
|
|
$C$9 |
y |
0 |
2,560975605 |
|
|
|
|
$D$9 |
z |
0 |
6,158536593 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Korlátozó
feltételek |
|
|
|
|
||
|
|
Cella |
Név |
Cellaérték |
Képlet |
Status |
Eltérés |
|
|
$B$15 |
x+y+z
≤ 10, Bal oldal |
10 |
$B$15<=$D$15 |
Éppen |
0 |
|
|
$B$16 |
2x-y
≥ 0, Bal oldal |
0 |
$B$16>=$D$16 |
Éppen |
0 |
Megjegyzést
csak a „Korlátozó feltételek” „Status” és „Eltérés” sorai érdemelnek. Az
„Eltérés” az optimális megoldáshoz tartozó baloldal és a jobboldal közti
eltérés(változó) értékét mutatja. A „Status” egyenlőtlenségek esetén akkor
„Éppen”, ha a baloldal eléri a jobboldalt, tehát ha az adott korlátozó feltétel
határán vagyunk. Egyéb esetekben a „Status” „Bőven”.
Tekintsük
az „Érzékenységjelentés” munkalapot:
|
Microsoft
Excel 11.0 Érzékenység jelentés |
|
|||
|
Munkalap:
[NLPSolver.xls]Munka1 |
|
|||
|
Készült:
2009.01.09. 11:07:50 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
Módosuló
cellák |
|
|
||
|
|
|
|
|
Redukált |
|
|
Cella |
Név |
Végérték |
gradiens |
|
|
$B$9 |
x |
1,280487802 |
0 |
|
|
$C$9 |
y |
2,560975605 |
0 |
|
|
$D$9 |
z |
6,158536593 |
0 |
|
|
|
|
|
|
|
Korlátozó
feltételek |
|
|
||
|
|
|
|
|
Lagrange |
|
|
Cella |
Név |
Végérték |
multiplikátor |
|
|
$B$15 |
x+y+z
≤ 10, Bal oldal |
10 |
-12,80487561 |
|
|
$B$16 |
2x-y
≥ 0, Bal oldal |
0 |
5,865853071 |
A
redukált gradiens nemnulla változókhoz tartozó komponensei optimális esetben
nullák kell, hogy legyenek. A Lagrange multiplikátorok a feladat Lagrange
duálja optimális megoldásvektora megfelelő koordinátáinak (-1)-szeresét
mutatják.
Végül
nézzük a „Határok jelentés”-t:
|
Microsoft
Excel 11.0 Határok jelentés |
|
|
|
|
|||||
|
Munkalap:
[NLPSolver.xls]Határok jelentés 1 |
|
|
|
|
|||||
|
Készült:
2009.01.09. 11:07:50 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Cél |
|
|
|
|
|
|
|
|
|
Cella |
Név |
Végérték |
|
|
|
|
|
|
|
|
$C$12 |
f=
x^2… |
-67,22560976 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Módosuló |
|
|
Alsó |
Cél |
|
Felső |
Cél |
|
|
Cella |
Név |
Végérték |
|
határ |
eredmény |
|
határ |
eredmény |
|
|
$B$9 |
x |
1,280487802 |
|
1,28048782 |
-67,22560976 |
|
1,28048782 |
-67,22560976 |
|
|
$C$9 |
y |
2,560975605 |
|
0 |
-12,85172516 |
|
2,56097565 |
-67,22560976 |
|
|
$D$9 |
z |
6,158536593 |
|
0 |
11,63370012 |
|
6,15853653 |
-67,22560976 |
Ez esetben az
„Alsó/Felső határ” és a megfelelő „Cél(függvény) eredmény” a
következőkre utal. Az adott optimális megoldásból kiindulva, egy-egy
változót milyen határok közt tudunk elmozdítani úgy, hogy a korlátozó
feltételek továbbra is teljesüljenek, és a határokon felvett változóértékek
mellett mekkora a célfüggvény értéke.
Függelék a Solver telepítéséhez
Szokásos
telepítés esetén az Excel nem rakja fel a Solvert a számítógépünkre, ezért
szükség lehet ennek a pótlólagos hozzáadására. Ekkor a teendőink a
következők.
Rakjuk
be az Office telepítőlemezt, majd índítsuk el a Setup programot (ha ez
automatikusan nem történne meg). A megjelenő ablakban
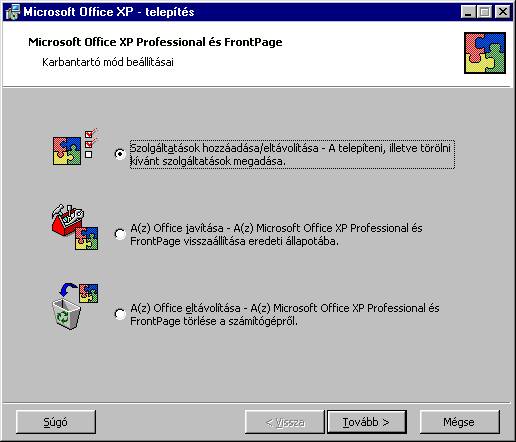
válasszuk a „Szolgáltatások
telepítése/eltávolítása” pontot, majd menjünk tovább. Itt a „Solver” mellet
levő ikont állítsuk a „Sajátgépről fut” vagy „Minden sajátgépről
fut” állapotra:
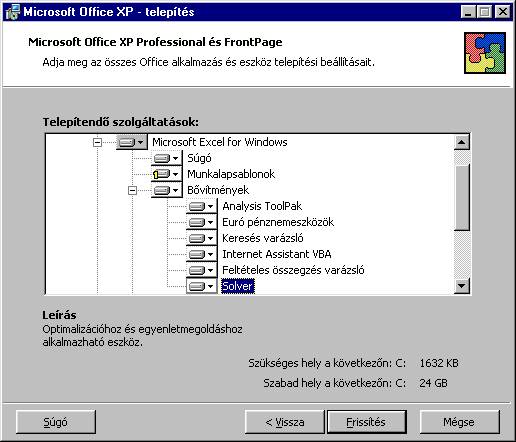
Majd
a „Közös Office szolgáltatások”-on belül aktivizáljuk a a „Visual Basic for
Applications” szolgáltatást is:
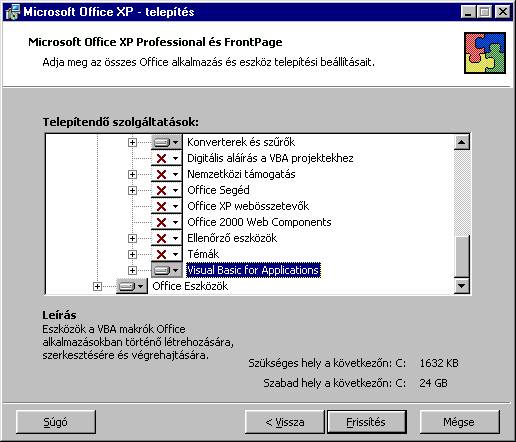
Ezután
a „Frissítés” gomb megnyomásával befejezhetjük a telepítést.