I. Bevezetés

• Halmazelméleti és logikai alapfogalmak.
• Algebrai muveletek. A valós számok.
• Cantor axióma és a Dedekind tétel (korlátos számhalmaz, sup H, inf H).
• Binomiális együtthatók, binomiális tétel. Bernoulli egyenlõtlenség.

• Valós számsorozatok korlátossága és konvergenciája.
• Mûveletek konvergens számsorozatokkal, egyenlõtlenségek. Rendõrelv.
• Nevezetes sorozatok (aⁿ, 2ⁿ/n, 2ⁿ/n!, a^1/n, n^1/n).
• Monoton és korlátos sorozatok konvergenciája.
• Nevezetes sorozatok ((1+1/n)ⁿ, (1+a/n)ⁿ).
• Rekurzív számsorozatok.
• Torlódási pont, limsup a_n, liminf a_n. Divergens sorozatok.
• Bolzano-Weierstrass kiválasztási tétel. Cauchy konvergencia kritérium.

• Valós számsorok konvergenciája, Cauchy kritérium.
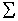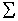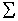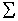• Nevezetes sorok. (1/n, qⁿ, 1/n!, (-1)ⁿ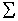1/n, 1/n)
• Pozitív tagú sorok konvergencia kritériumai (majoráns, minoráns, hányados és gyökkkritérium)
• Váltakozó elõjelû sorok. Leibniz sorok.
• Abszolút konvergencia, feltételes konvergencia.
• Mûveletek konvergens sorokkal. Zárójelek elhagyása, betétele.
• Numerikus sorok összegének közelítõ értéke, a hiba becslése.

 

• A függvény fogalma. Mûveletek függvények között.
• Paritás, monotonitás, periodikusság.
• Egyváltozós valós függvények határértéke.
• Átviteli elv. Cauchy kritérium.
• (cf), (f+g), (fg), ( 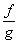) határértéke
• Példák. sgn x, [x], {x}, Dirichlet típusú függvények.
• Szakadások osztályozása, folytonosság.
• Folytonos függvények tulajdonságai.
• Bolzano tétel, példák.
• Kompakt halmazon folytonos függvények tulajdonságai. (Nyílt, zárt, kompakt halmaz fogalma.)
• Weierstrass tételek és alkalmazásai.
• Egyenletes folytonosság fogalma, elégséges feltétel.
• Példák az egyenletes folytonosság tétel alkalmazására.
• A 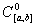  mint lineáris tér.

• Differenciálhatóság, derivált (geometriai és fizikai jelentése).
• Szükséges és elégséges feltétel a differenciálhatóságra.
• Érintõ egyenlete, differenciál fogalma.
• Deriválási szabályok.
• Az (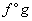) összetett függvény deriváltja.
• Egy-egyértelmû leképezés, inverz függvény.
• Inverz függvény differenciálhatósága, deriváltja.
• Polinomok, racionális törtfüggvények, trigonometrikus függvények deriváltja.
• Irracionális függvények deriváltja.
• A trigonometrikus függvények inverzei (ábrázolás, tulajdonságok, derivált).
• Az exponenciális és logaritmus függvény tulajdonságai, deriváltjai.
• A hiperbolikus függvények és inverzeik definíciója, tulajdonságai, ábrázolása.
• Nevezetes határértékek.
  , , , , , , , 
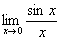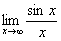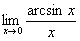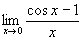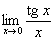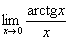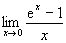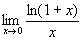
• A lokális szélsõérték létezésének szükséges feltétele differenciálható függvényeknél: f'(x₀)=0 (belsõ pontban).
• Középérték-tételek (Rolle, Lagrange, Cauchy).
• L'Hospital szabály. Példák a különbözõ határozatlan alakokra.
• Logaritmikus deriváltak.
• Implicit függvény deriváltja.
• Magasabbrendû deriváltak.
• Nyílt intervallumon differenciálható függvények tulajdonságai.
• Monotonitás, szigorú monotonitás feltételei intervallumon.
• Konvexitás, konkávitás feltételei.
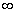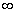• Lineáris aszimptota a +-ben illetve a --ben.
• Függvényvizsgálat.
• Korlátos és zárt intervallumon értelmezett folytonos függvény abszolút szélsõértékeinek meghatározása.
• Lokális tulajdonságok (növekedés, csökkenés, szélsõérték, inflexió).
• Szükséges feltételek illetve elégséges feltételek a lokális tulajdonságok teljesülésére.
• Implicit egyenletet kielégítõ differenciálható függvények lokális tulajdonságai.
• Paraméteres megadású görbék vizsgálata, ábrázolása.
• Polár koordinátákban adott görbék érintõ egyenesének egyenlete.

• Primitív függvény. Határozatlan integrál.
• Az integrálszámítás alaptétele.
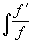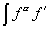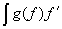• , ,  típusú integrálok.
• Az integrálás technikája.
• Parciális integrálás.
• Integrálás parciális törtekre bontással.
• Integrálás helyettesítéssel.
• Racionális törtfüggvény integrálására visszavezethetõ helyettesítések: t=e^x, t=tg(x/2).
• meghatározása helyettesítéssel.
• A Riemann integrálhatóság, illetve a határozott integrál fogalma.
• Az F felosztáshoz tartozó alsó, felsõ közelítõ összeg, integrál közelítõ összeg, oszcillációs összeg.
• A Riemann integrálhatóság szükséges és elégséges feltételei.
• Integrálható függvények terei. (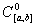, korlátos és monton függvények stb.)
• A Riemann integrál mint lineáris funkcionál.
• A Riemann integrál tulajdonságai, az integrálközép.
• Az integrálfüggvény folytonossága, differenciálhatósága. 
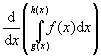
• A Newton-Leibniz formula. Newton-Leibniz formula alkalmazása integrál transzformáció és parciális integrálás esetén.
• L'Hospital szabály alkalmazása integrál függvények hányadosa esetén.
• Improprius integrál, ha az integritási tartomány [a, 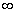 ) vagy (- 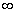,a], az integrandus függvény korlátos.
• Improprius integrál, ha az integritási tartomány [a,b] és az integrandus függvény nem korlátos az egyik végpontban.
• Improprius integrálokra vonatkozó majoráns, minoráns, kritérium.
• Improprius integrálokra vonatkozó Cauchy kritérium.
• Improprius integrálok abszolút és feltételes konvergenciája.
• Numerikus sor konvergenciájának eldöntésére vonatkozó integrál kritérium.
• Numerikus sor összegének közelítõ meghatározása, a hiba becslése integrál kritériummal.

VII. Numerikus sorozatok és sorok nagyságrendje

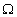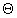• Sorozatok alsó és felsõ becslése, az O(a_n), (a_n), (a_n) szimbólumok használata.
• Rekurzív sorozatok nagyságrendje.
• Sorozatok aszimptotikus egyenlõsége.
• Stirling formula. Példák a Stirling formula alkalmazására.
• A binomiális együtthatók nagyságrendje.
• Aszimptotikusan azonos sorok konvergenciája. (Numerikus sorok ekvivalenciája.)

Budapest, 1999. november