Gyakorló Óra feladatai:

Első Feladat
Második Feladat
Harmadik Feladat
Negyedik Feladat
Ötödik feladat

Első Feladat

Írjunk olyan tobbfelenKozelit nevű szkriptet aminek van 1 bemenete (n), ami megmondja hány helyen közelítjük az exp(-x^2) függvényt a [-5,5] intervallumon. Opcionális második paramétere lehet 'spline', 'polyfit' és 'both' ami a közelítés módját adja meg. 'both' esetén mindkét módszerrel közelít. Ábrázoljuk a kapott eredményeket.

type('tobbfelenKozelit.m')
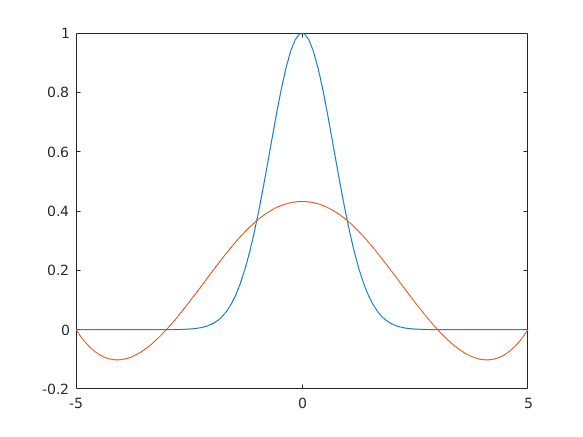
tobbfelenKozelit(6)

function tobbfelenKozelit(n,tipus)
    x=linspace(-5,5,n);
    y=exp(-x.^2);
    t=linspace(-5,5);
    if (nargin==1)||strcmp(tipus,'spline')
       plot(t,exp(-t.^2),t,spline(x,y,t))
    elseif strcmp(tipus,'polyfit')
       eho=polyfit(x,y,n-1);
       plot(t,exp(-t.^2),t,polyval(eho,t))
    else
       eho=polyfit(x,y,n-1);
       plot(t,exp(-t.^2),t,polyval(eho,t),t,spline(x,y,t),'m-')
    end
end

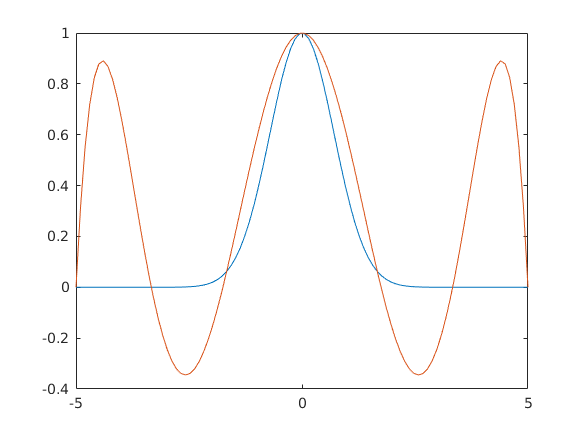
tobbfelenKozelit(7,'polyfit')

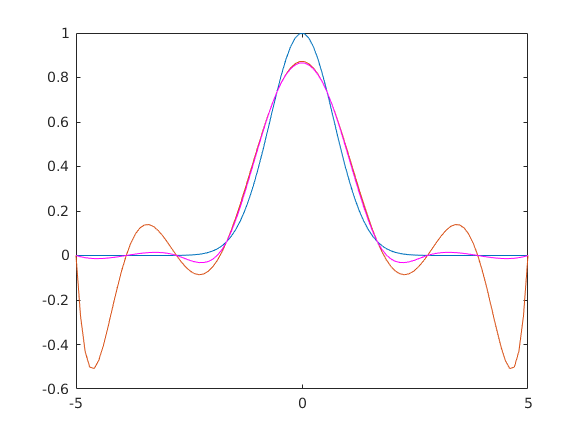
tobbfelenKozelit(10,'both')

Második Feladat

Egy új, kísérleti szárnnyal mérik a fogyasztás csökkenését repülőknél. A kísérlet drón mindig ugyanazt a pályát járja be. A pályákon rendre:

4, 4.5, 4.7, 5, 5.1, 3.7, 4.2, 4.4, 5, 5.1, 3.9, 4.1, 4.3, 4.4

liter fogyasztást mértek. Végezzünk T-próbát arra vonatkozóan, hogy a fogyasztűs várható értéke megegyezik-e 4.9 literrel? Ha különbözik milyen szignifikancia szinten különbözik? Ha meg akarnák ismételni a fenti kísérletet. Hány repülést kéne végrehajtaniuk, hogy legalább 99%-os biztonsággal hasonlóan jó eredményt kapjanak?

dronAdat=[4, 4.5, 4.7, 5, 5.1, 3.7, 4.2, 4.4, 5, 5.1, 3.9, 4.1, 4.3, 4.4];
[h,pErtek]=ttest(dronAdat,4.9)

h =

     1


pErtek =

    0.0034

A 1-es hipotézisre döntünk (a default 0.05 szignifikancia szint mellett). A p-érték 0.003, tehát 0.3% szignifikancia szint alatt döntenénk úgy, hogy egyenlő lenne a kettő.

sampsizepwr('t',[mean(dronAdat),std(dronAdat)],4.9,0.99)

ans =

    23

Harmadik Feladat

Egy fülemülefaj magyarországon, és a környező országokban is elterjedt. Az itthoni ornitológusok mintát vettek, hogy hány tojás van a fészkekben, az alábbi eredményeket kapták:

5, 5, 6, 6, 5, 4, 4, 6, 4, 5, 3, 7, 5

Romániában is elvágezték a kísérletet, és következőt mérték:

6, 5, 4, 4, 3, 3, 5, 5, 5, 6, 5, 6, 5

Vajon mindékt helyen ugyanolyan jól érzi magát a faj? Végezzünk kétmintás T-próbát, állapítsuk meg, hogy mekkora szgnifikancia melett különbözik a két minta!

fulemuleMinta1=[5, 5, 6, 6, 5, 4, 4, 6, 4, 5, 3, 7, 5];
fulemuleMinta2=[6, 5, 4, 4, 3, 3, 5, 5, 5, 6, 5, 6, 5];
[h,pErtek]=ttest2(fulemuleMinta1,fulemuleMinta2)

h =

     0


pErtek =

    0.5794

A 0-ás hipotézisre döntünk (nem különbözik a két minta). A p-érték 0.55 tehát 0.55-nél nagyobbnak kéne lennie a szig. szintnek, hogy különbőző legyen (ez azt jelentené, hogy az elsőfajú hiba ennél nagyobb).

Negyedik Feladat

Az alábbi szövegben számoljuk meg az "sz"-ek számát:

'A helyzete nem szerencsés. Apró szemcsés homokkal telve a füle, a nyelve.'

szoveg='A helyzete nem szerencsés. Apró szemcsés homokkal telve a füle, a nyelve.'
count(szoveg,'sz')

szoveg =

    'A helyzete nem szerencsés. Apró szemcsés homokkal telve a füle, a nyelve.'


ans =

     2

Másik megoldás:

logvect1=szoveg=='s';
logvect2=szoveg=='z';
sum(logvect1(1:end-1)&logvect2(2:end))

ans =

     2

Ötödik feladat

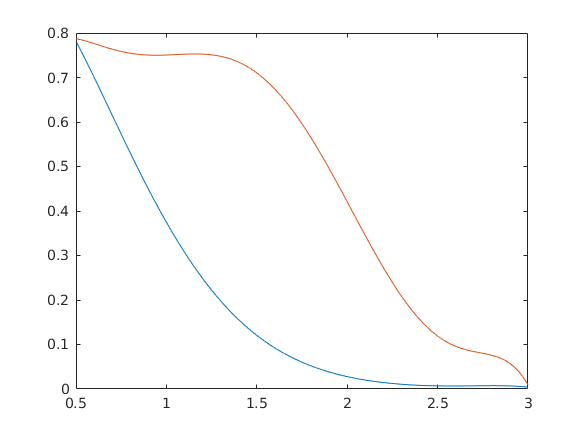
A "Testfile.xlsx" három oszlopot tartalmaz az első oszlopban van a hely ahol a második két függvény értékeit számoltam. Sajnos a két függvényt nagyon nehéz számolni, csak numerikusan közelített értékeim vannak amik nem mindig jók, viszont tudom, hogy a függvényeknek monoton csökkenőnek kell lenniük. Tegyük őket monotonná, és ábrázoljuk az eredényt!

[szam,szoveg,mind]=xlsread('Testfile.xlsx');
for i=1:100
    if ischar(mind{i,1})
        x(i)=str2num(mind{i,1});
    else
        x(i)=mind{i,1};
    end
end
for i=1:100
    y1(i)=str2num(mind{i,2});
end
for i=1:100
    y2(i)=str2num(mind{i,3});
end
plot(x,[y1;y2])

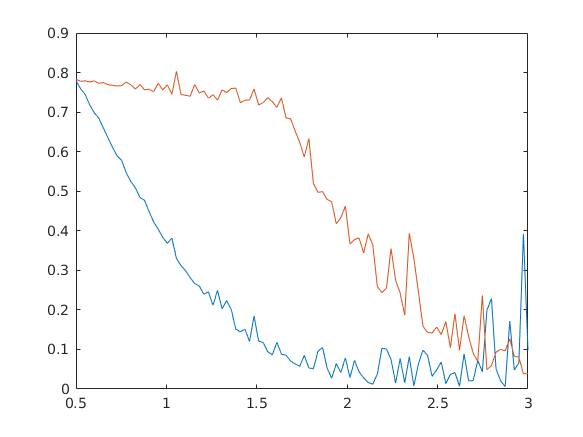
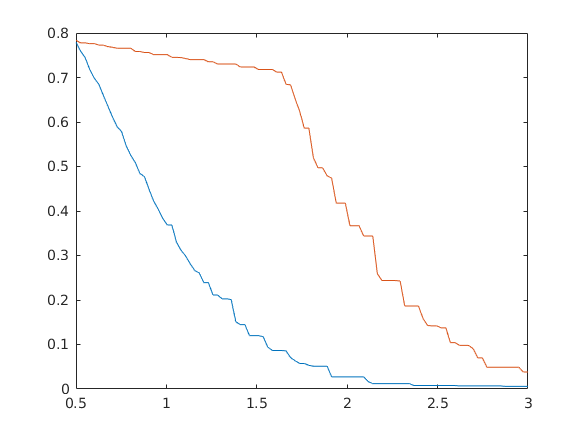
type('simit.m')
plot(x,[simit(y1);simit(y2)])

function v=simit(v)
minertek=v(1);
for i=1:length(v)
    if v(i)<minertek
        minertek=v(i);
    else
        v(i)=minertek;
    end
end