A "nargin" beépített függvény és különbőző ábrázolási módok

Contents

A "nargin" függvény

Mostanra már tapasztalhattuk, hogy a beépített függvények zömét, sokféleképp meg lehet hívni. A nargin függvény megadja hány paraméterrel hívták meg a függvényünket és így a paraméterek számától fühggően másképp működhet függvényünk.

Első közös feladat

Írjunk egy "bemenet" nevű függvényt amit 1, 2, vagy 3 (a,b,c) számmal hívhatunk meg. Ha egy bemenete (a) van akkor a kimenete legyen a^2, ha két bemenete (a,b) van akkor a kimenet legyen a+b, ha három bemenete van (a,b,c) akkor a kimenet legyen a+b*c.

type('bemenet.m')

function kimenet=bemenet(a,b,c)
    if nargin==1
        kimenet=a^2;
    elseif nargin==2
        kimenet=a+b;
    elseif nargin>2
        kimenet=a+b*c;
    end
end

Első Házi feladat

Írjunk "specAtlag" nevű függvényr, aminek bemenete lehet (v,a,b). Ha egy paramáterrel (v) hívjék meg akkor a kimenet legyen v átlaga, ha két paraméterrel (v,a) akkor legyen a kimenet az "a"-nál nagyobb elemek átlaga, ha három paraméterrel hívják meg akkor a kimenet legyen az "a"-nál nagyobb "b"-nél kisebb elemek átlaga.

function ki=specAtlag(v,a,b)
    if nargin==1
        ki=mean(v);
    elseif nargin==2
        ki=mean(v(v>a));
    else
        ki=mean(v(v>a&v<b));
    end
end

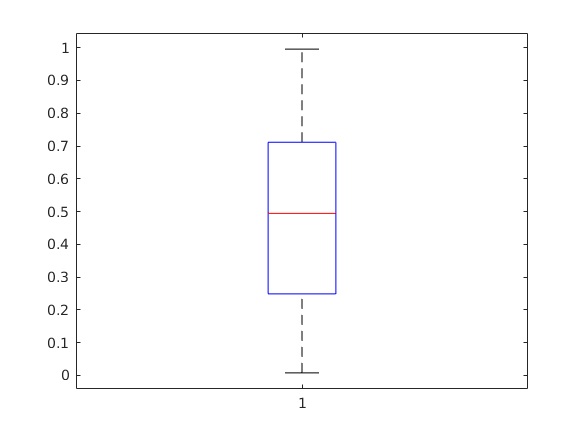
Boxplot

Múlt héten láthattuk a hogyan kell histogrammmot készíteni. Hasonló adatok ábrázolására jó a "boxplot" parancs. a boxplot a megadott értékeket sorbarendezi a középső értéket (mediánt) pirossal rajzolja ki- Kékkel kirajzol egy olyan intervallumot aminek az alja azt jelöli, hogy annál az elemeknek csak a negyede van lejebb és a teteje az intervallumnak azt jelenti, hogy annál csak az elemek egynegyede van feljebb. A fekete "karokat" a kék intervallum másfélszeresénél húzza meg, kivéve ha a minimum/maximum annál nagyobb/kisebb, mert akkor ott.

v=rand(1,100);
boxplot(v);

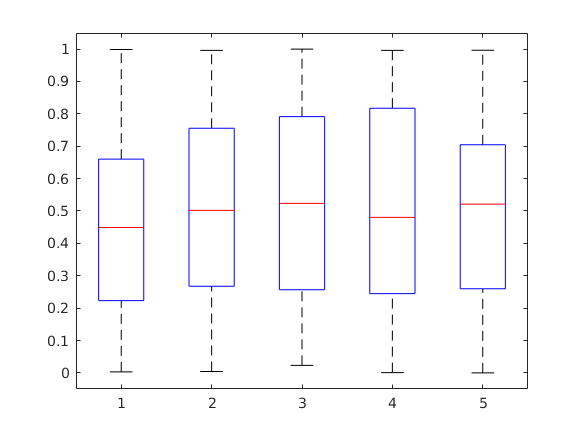
Ha mátrix a bemenet akkor oszloponként csinál boxplot-ot

M=rand(100,5);
boxplot(M);

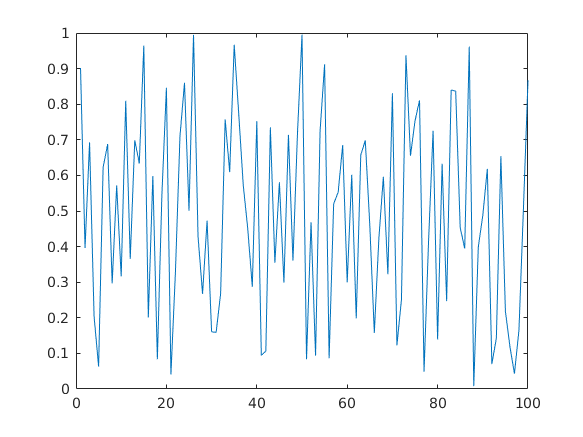
A plot parancs

A plot parancsot -ha egy bemenettel hívjuk- akkor e numerikus vektor megjelenítésére lehet használni pl

plot(v)

Vagy ha létrehozunk egy 100 elemú vektort aminek elemei -10 és 10 között vannak egyenletesen

t=linspace(-10,10,100);

akkor ezekre az elemekre alkalmazva egy függvényt a függvényértékeket is megjeleníthetjük.

plot(sin(t))

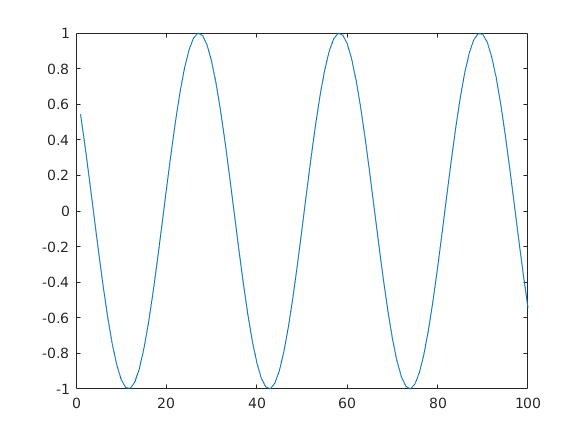
Látjuk hogy az első elem a szinusz függvény a -10 helyen

sin(-10)

ans =

    0.5440

A második a szinusz függvény a -9.798 helyen (ami a t vektor második eleme) stb. Egy kicsit zavaró, hogy az x tengelyen nem -10-től 10-ig mennek a számok. Ezen könnyen segíthetünk:

plot(t,sin(t))

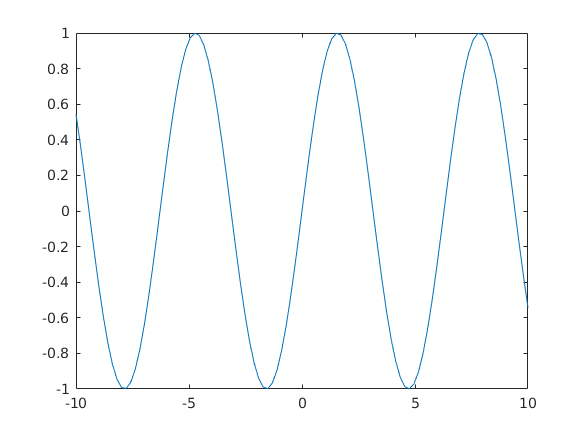
A plot parancsot 2 vektorral meghívva az első vektort mindig az ábrázolandó pontok x koordinátájának tekinti, a második vektort az y koordinátáknak.

Parametrikus görbék megadása

Így viszont paramterikus görbéket is megadhatunk. (Ezt úgy kell elképzelnünk, hogy egy paramétert, például az időt, véltoztatjuk és minden időpillanatban megmondjuk hol van a ceruza hegyének x és y koordinátája.)

Egy körnek például ez a parametrikus megadása: x=cos(t) y=sin(t). Így kell kirajzoltatni:

plot(cos(t),sin(t))

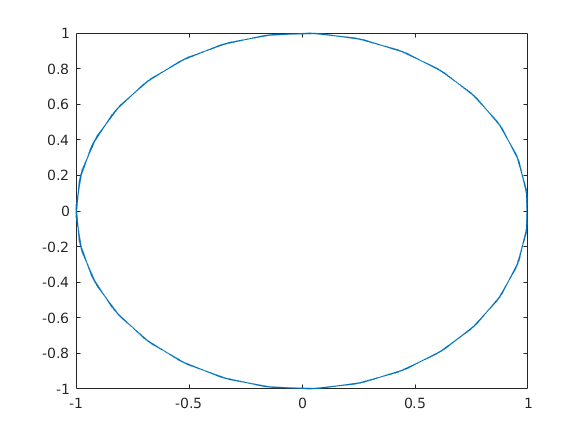
Ez a kör egy kicsit nyomott a következő paranccsal rendes körré változtathatjuk, úgy hogy az y/x tengelyen azonossá tesszük a távolságokat:

plot(cos(t),sin(t))
axis('equal')

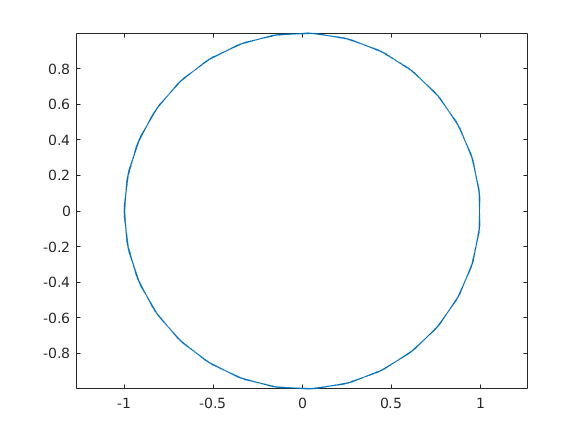
Harmadik paraméterként megadhatjuk hogy milyen módon rajzolja ki a görbénket a következő parancs:

plot(cos(t),sin(t),'r+')

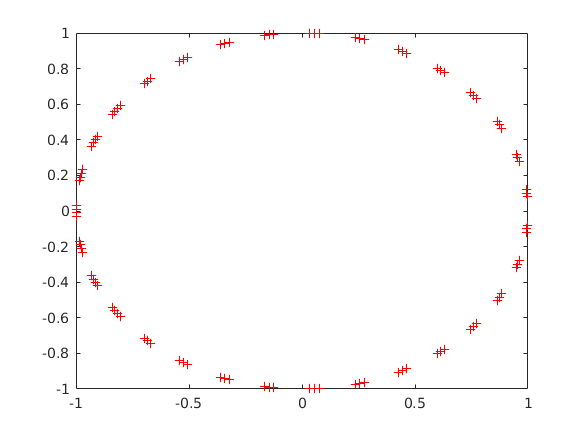
példáult piros (red) plusszokat rak a pontok helyére és nem köti össze őket. A következő:

plot(cos(t),sin(t),'k-.')

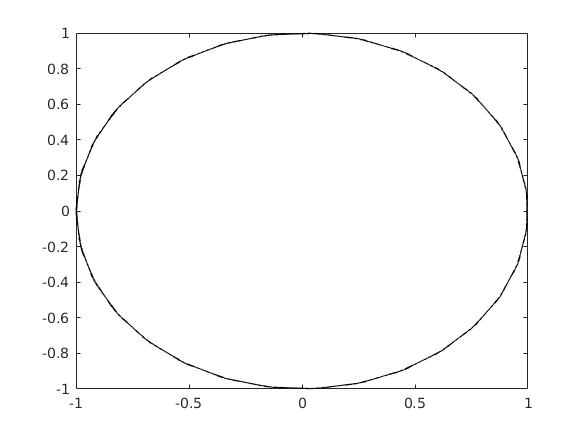
pedig fekete (blacK) pont-vonallal köti össze őket. Az összes vonaltípusról a plot parancs helpjének LineSpec része ad részletes útmutatást. A tengelyeknek is adhatunk nevet, és az ábrának is:

plot(cos(t),sin(t),'bo-')
xlabel("x koordinata")
axis('equal')
ylabel("ez a magassag")
title("Ez egy kör")

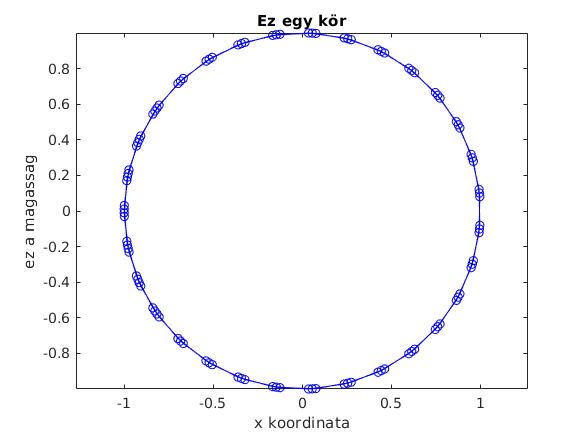
A hold on paranccsal további görbéket rajzolhatunk ugyanabba az ábrába

hold on
t=linspace(0,2*pi,100);
plot(t.*cos(t)/2,t.*sin(t)/2)
hold off

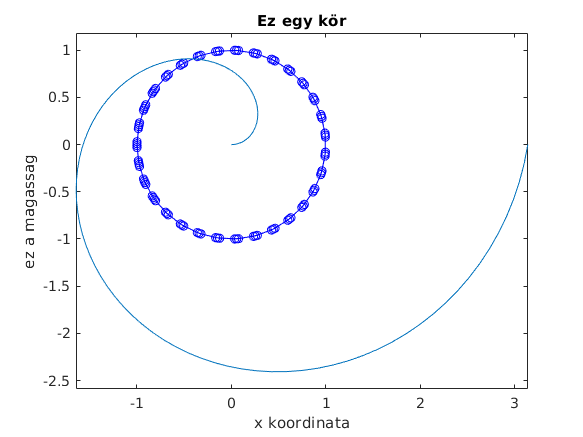
A text paranccsal feliratikat helyezhetünk el az ábrán.

t=linspace(0,10*pi,1000);
plot(t.*cos(t),t.*sin(t))
axis('equal')
hold on
plot(cos(t),sin(t))
plot(0,0,'b+')
text(0,0,"Ez a kozepe")
hold off

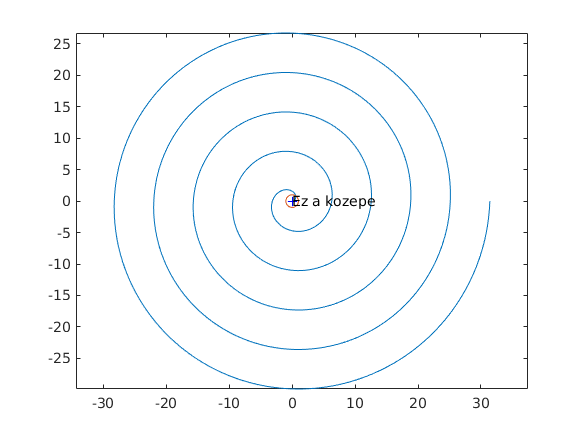
Második házi feladat

Készítsünk ábrát a cikloisról. A ciklois azt mutatja, hogy egy r sugarú keréknek az a pontja ami nullában pont a talajt érinti milyen pályán mozog. A képlete x=r(t-sin(t)) y=r(1-cos(t)). A g0rbe legyen k;k folytonos vonallal megrajzolva. Az x tengelyen legyen az a felirat hogy "Idő", az y tengelyen legyen az a felirat, hogy "Pálya", az Origóba legyen odaírva, hogy "A pálya kezdőpontja". Az elkészült ábrákat mentsltek el és küldéjtek a házi feladatoknak fentartott e-mail címre.

Epiciklois gyakorló feladat

A ciklois egyik általánosítása az epiciklois ahol egy kör egy másikon gurul. Képlete x=r*(k+1)*(cos(t)-cos((k+1)*t)/(k+1)) y=r*(k+1)*(sin(t)-sin((k+1)*t)/(k+1)) ahol k a két kör aránya.

t=linspace(-100,100,3000);
r=3;
k=37/21;
plot(r*(k+1)*(cos(t)-cos((k+1)*t)/(k+1)),r*(k+1)*(sin(t)-sin((k+1)*t)/(k+1)),'m-')
axis('equal')

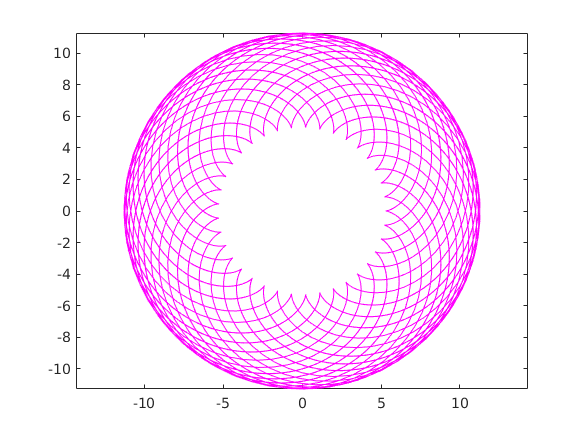
A hipociklois-nál az egyik kör a másik körnek a belsején gurul képlete x=r*(k+1)*(cos(t)-cos((k+1)*t)/(k+1)) y=r*(k+1)*(sin(t)+sin((k+1)*t)/(k+1))

hold on
r=2;
k=7/3;
plot(r*(k+1)*(cos(t)-cos((k+1)*t)/(k+1)),r*(k+1)*(sin(t)+sin((k+1)*t)/(k+1)),'b-')
hold off

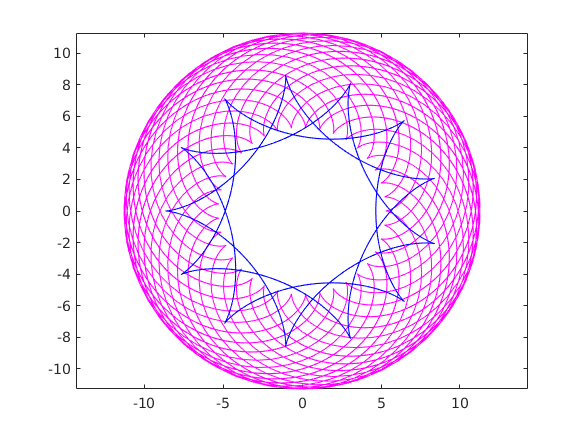
snapnow

Published with MATLAB® R2019a