Interpoláció

Contents

A gyakorlatban sokszor előfordul, hogy egy ---akár ismeretlen--- függvénynek csak néhány ponjában ismerem az értékét de szeretnék egy közelítő fügvvényt adni az eredetire.

Lineáris Interpoláció

Ez a legegyszerűbb módszer, a két legközelebbi függvényértéken kereszült húzok egy egyenest és így közelítem a függvényértéket (töröttvonallal öszekötöm a pontokat)

x=[0,pi/3,pi/2] % alappontok itt tudom a függvény értékét
y=[0,sqrt(3)/2,1]; % függvényértékek (ezeket mérem)
hol=0.3; % melyik pontban vagyok kiváncsi a közelítés értékére
ert=interp1(x,y,hol) % A közelítés értéke

x =

         0    1.0472    1.5708


ert =

    0.2481

Ez gyors eredményt ad, csrébe viszont nem túl pontos. Itt például a szinusz függvényt közelítjük. Kirajzolhatkjuk azt is, hogy mi lenne a valódi érték.

plot(x,y,hol,ert,'r+',hol,sin(hol),'go')
legend('lineáris interpoláció','közelített függvényérték','valódi függvényérték')

Spline interpoláció

A spline interpolációnál alacsony fokú függvényeket "fűzünk" össze amik átmennek az adott pontokon, és ahol kapcsolódnak ott a deriváltjuk azonos (nincs bennük törés)

ert2=spline(x,y,hol);
t=linspace(0,1);
plot(t,sin(t),hol,ert,'r+',hol,ert2,'go')
legend('valódi függvény','lineárisan közelített függvényérték','spline-al közelített függvényérték')

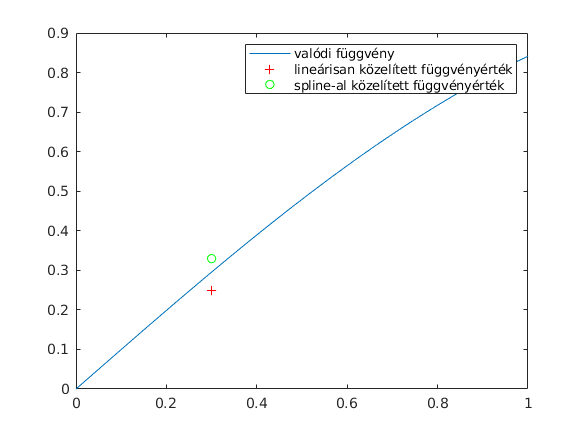
Megnézhetjük hogy mivel közelítjük a valódi függvényt:

sokertek=spline(x,y,t);
plot(t,sin(t),t,sokertek,hol,ert,'r+',hol,ert2,'go')
legend('valódi függvény','spline','lineárisan közelített függvényérték','spline-al közelített függvényérték')

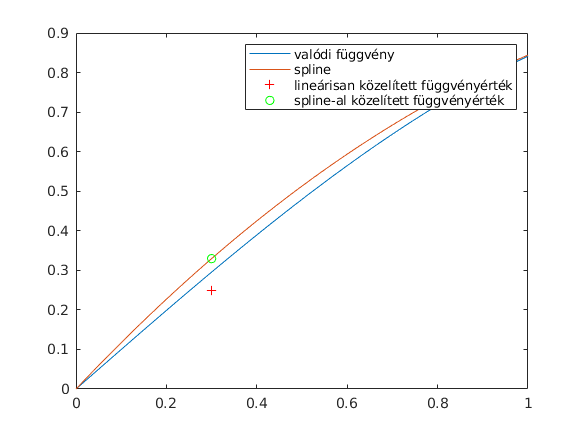
Ha nagyobb intervallumon nézzük akkor látjuk, hogy a megadott három ponton átmegy a spline.

t=linspace(0,pi/2);
sokertek=spline(x,y,t);
plot(t,sin(t),t,sokertek,'r',x,y,'mo')
legend('valódi függvény','spline','A közelített pontok')

Adott fokszámú polinom illesztése

Azt is csinálhatjuk, hogy a megadunk n pontot, és utána megkeressük azt az n-1 fokú polinomot ami átmegy a megadott pontokon.

egyutthatok=polyfit(x,y,2) % A polyfit megadja a közelítő polinom együtthatóit
polyval(egyutthatok,hol) % A polyval az együtthatókból meghatározza az adott pont(ok)ban a ploinom értékét
t=linspace(-1,5);
plot(t,sin(t),t,polyval(egyutthatok,t))
legend('Eredeti függvény','illesztett függvény')

egyutthatok =

   -0.3636    1.2077    0.0000


ans =

    0.3296

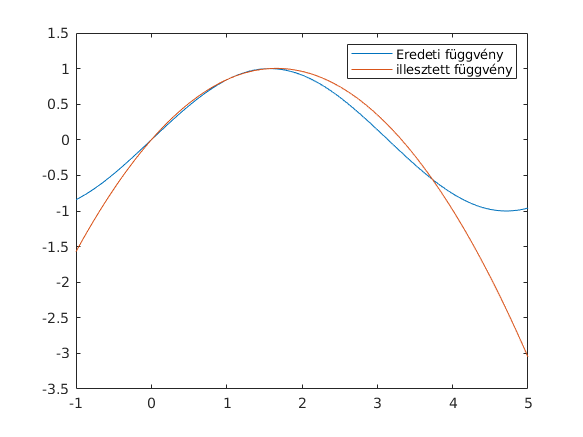
órai Feladat

Írjunk olyan scriptet ami közelíti 1/(1+x^2) függvényt, a [-5,5] intervallumon. Bemenete legyen egy szám ami megadja hogy hány pontban közelítem. polyfittel ad egy n-1-ed fokú polinomközelítést. Majd kirajzolja az eredeti és a közelítő függvényt.

function kozelit(n)
x=linspace(-5,5,n);
y=1./(1+x.^2);
ehato=polyfit(x,y,n-1);
t=linspace(-5,5);
plot(t,1./(1+t.^2),t,polyval(ehato,t),x,y,'go');
end

kozelit(5)

kozelit(15)

Warning: Polynomial is badly conditioned. Add points with distinct X values,
reduce the degree of the polynomial, or try centering and scaling as described
in HELP POLYFIT. 

Házi feladat:

írjunk olyan scriptet ami a [0.5,1,1.5,2,2.5,3,3.5] alappontokban a [3.27,6.1,9.7,12.9,15.1,19.4,21.3] értékekekt a legjobban közelítő egyenest adja meg. A script visszatérő értéke legyen az egynes meredeksége.

Bónusz házi feadat:

Írjunk jobbkozelito nevű függvényt ami úgy működik, hogy ha 10-nél több pontot adok meg, akkor spline-nal közelít és ábrázolja a végeredményt.

Published with MATLAB® R2019a