2. Zh megoldások
Contents
Első feladat
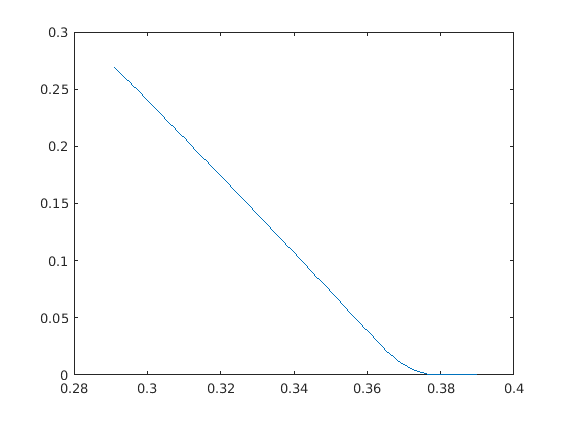
Írjunk ketFelenKozelit nevű polimorf függvényt aminek ha két beme- nete (n,k) van akkor az x + cos(x) + 1/2 cos(2x) + 1/3 cos(3x) függvényt közelíti spline-al a [0,2]-őn n pontban, és k-ad fokú polinommal közelí- ti 10 pontban a [2,4]-en. Ha a harmadik bemenet ’forditva’ akkor az intervallumokat fordítsa meg (és [2,4]-en közelítsen spline-nal és [0,2]-őn polinommal). Ábrázoljuk a közelítést mindkét intervallumon egyszerre!
type('ketFelenKozelit.m')
function ketFelenKozelit(n,k,mod)
if nargin ==3 && strcmp(mod,'forditva')
xspl=linspace(2,4,n);
tspl=linspace(2,4);
xpol=linspace(0,2,10);
tpol=linspace(0,2);
else
xspl=linspace(0,2,n);
tspl=linspace(0,2);
xpol=linspace(2,4,10);
tpol=linspace(2,4);
end
yspl=xspl+cos(xspl)+(1/2)*cos(2*xspl)+(1/3)*cos(3*xspl);
ypol=xpol+cos(xpol)+(1/2)*cos(2*xpol)+(1/3)*cos(3*xpol);
eho=polyfit(xpol,ypol,k);
plot(tspl,spline(xspl,yspl,tspl),tpol,polyval(eho,tpol))
end
ketFelenKozelit(4,4)
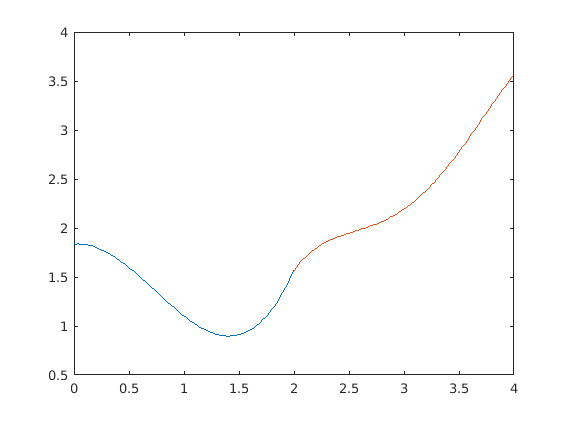
ketFelenKozelit(5,6,'forditva')
Második feladat
Generáljunk 1000 darab véletlen egész számot 1 és 10 között. Számítsuk ki ezeknek az átlagát és szórását! Végezzünk T-próbát arra nézve, hogy ezen vektor várható értéke megegyezik-e 5,5-el! Interpretáljuk a használt függvény kimenetét: mekkora a p-érték, mire döntünk és mikor (milyen szignifikancia szinten) változtatnánk a döntésünkön?
randvekt=randi(10,1,1000);
[h,pertek]=ttest(randvekt,5.5) % Mivel pertek nagyobb mint 5% ezért a H0-t fogadjuk el vagyis a várható % értéke megegyezik 5,5-el! % Ha a szignifikancia szint nagyobb lenne mint a pertek akkor arra % döntenénk, hogy különböznek
h =
0
pertek =
0.9566
Harmadik feladat
hug=[2, 3, 3, 2, 4, 5, 5, 1, 0, 2, 5, 2, 4, 2]; mar=[1, 1, 2, 1, 3, 1, 2, 4, 2, 3, 3, 2, 0, 3]; [h,pertek]=ttest2(mar,hug)
h =
0
pertek =
0.1061
Nem különböznek, mert a p-érték nagyobb mint 5%. Ha a szignifikancia szint 10,61%-nál nagyobb lenne akkor döntenénk úgy, hogy különböznének.
Negyedik feladat
Írjunk palindromE(s) függvényt ami eldönti egy adott s karakter vektorról, hogy palindrom-e (ehhez hagyjuk figyelmen kívül a space-eket és irásjeleket). (Bónusz: hagyjuk figyelmen kívül a kis és nagybetűt is.)
type('palindromE')
function ki=palindromE(s)
csakbetuk=s(isletter(s));
if strcmpi(csakbetuk,csakbetuk(end:-1:1))
ki=true;
else
ki=false;
end
end
s1='keretkarakterek'; s2='indul a görög aludni.'; s3='Indul a görög aludni.'; palindromE('Haha')
ans = logical 0
palindromE(s1)
ans = logical 1
palindromE(s2)
ans = logical 1
palindromE(s3)
ans = logical 1
Ötödik feladat
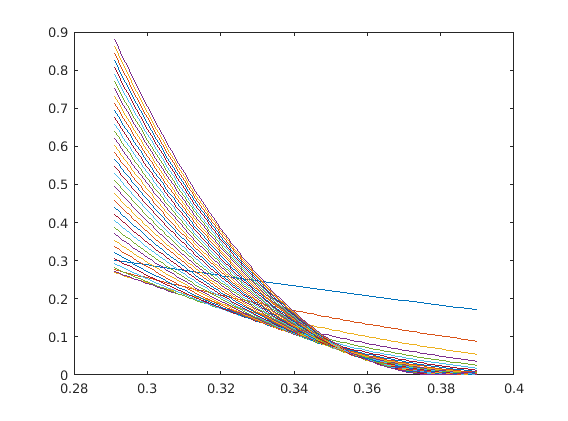
A ’T2.xlsx’ fájl 40 függvény adatait tartalmazza. Az első oszlop tartal- mazza az alappontokat, a többi oszlop a függvények ezen alappontokban számított értékeit. Ábrázoljuk a 40 függvényt egy ábrán.
[szam,szoveg,mind]=xlsread('T2.xlsx'); for i=1:100 for j=1:40 M(i,j)=str2num(mind{i,j}); end end plot(M(:,1),M(:,2:end))
Szorgalmi feladat:
A 5. feladatban a 40 függvényt ábrázoljuk egy darab (keve- sebb mint 80 karkater hosszú) paranccsal, valamint egy ábrán ábrázoljuk a 40 függvény minimumát.
plot(M(:,1),min((M(:,2:end))'))