gyakorló feladatok III.

I. éves építőmérnökhallgatók számára

Matematika B1

1. Mi az alábbi implicit módon megadott függvények differenciálhányadosa?

a.) , b.) c.)

2. Adja meg az egyenletű ellipszis (1;1) pontbeli érintőjének egyenletét.

3. Írja fel azoknak az egyeneseknek az egyenletét, melyek érintik az egyenletű hiperbolát és párhuzamosak az egyenletű egyenessel.

4. Írja fel az alábbi görbék adott pontbeli érintőjének és normálisának egyenletét:

a.) 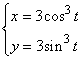, b.) .

5. Írja fel azoknak az egyenesnek az egyenletét, melyek átmennek a (3;0) ponton és érintik az paraméteres egyenletrendszerű ellipszist.

6. Egy körcikk kerülete 4,8 . Mekkora a kör sugara, ha a körcikk területe maximális?

7. Az cm sugarú félkörbe az átmérőn fekvő trapézt rajzolunk. Hogyan kell a trapéz adatait megválasztani, hogy a területe maximális legyen?

8. Határozza meg az adott kúpba írható maximális térfogatú henger adatait.

9. Határozza meg az egység sugarú gömbbe írható, maximális téfogatú kúp adatait.

11. Az parabola mely pontja van legközelebb a (0;6) ponthoz?

12. Vízszintes terepen állva a vízszintessel szöget bezáró irányban elhajítunk egy követ. mely értéke mellett fog tőlünk legtávolabb leesni a kő?

13.* Két ember egy vízszintes helyzetben lévő létrát visz. Derékszögben hajló folyosón legfeljebb milyen hosszú létrával tudnak bekanyarodmi, ha a folyosók szélessége 3m és 5m?

14. Határozza meg az alábbi görbék megadott pontjában a görbületet:

a.) , b.) , c.) .

15. Határozza meg az görbe legnagyobb görbületét.

16. Írja fel az alábbi függvények negyedfokú Taylor-polinomját az helyen:

a.) , b.) , c.) , d.) .

17. Írja fel az függvény körüli harmadfokú Taylor-polinomját.

18. Határozza meg a következő függvények közelítő értékét a harmadfokú Taylor-polinom segítségével és becsülje meg a hibát:

a.) b.) sh 0,3.

19. Közelítse e értékét a harmadfokú Taylor-polinom segítségével és becsülje meg a hibát.

20. Használja az függvény körüli harmadfokú Taylor-polinomját közelítő értékének kiszámítására.

21. Számítsa ki ln 1,1 értékét pontossággal.

22. Hanyadrendben érintkeznek az alábbi függvények az adott helyen?

a.) ; b.) ;

c.) ; d.).

hATÁROZATLAN INTEGRÁLOK:

1. ,

2.

3.

4.

5.

6.

7.

8.

9.

10.

11.

12.

13.

14.

15.

16.

17.

18.

19.

20.

21.

22.

23.

24.

25.

26.

27.

28.

29.

30.

31.

32.

33.

34.

35.

36.

37.

38.

39.

40.

41.

42.

43.

44.

45.

46.

47.

48.

49.

50.

51.

52.

53.

54.

55.

56.

57.

58.

59.

60.

61. Számítsa ki az alábbi határozott integrálokat:

a.) , b.) c.) , d.) .

62. Számítsa ki annak a parcellának a területét, melyet az alábbi görbék határolnak:

a.) x tengely, az egyenes és az ;

b.) ;

c.)

d.) , ennek az origón átmenő érintője, x tengely.

63. Forgassuk meg az előbbi példa a.) részében szereplő parcellát az x tengely körül és számítsuk ki a keletkezett forgástest felszínét és térfogatát!

64. Az asztroid paraméteres egyenletrendszere , .

Számítandó T, s, F, V, azaz a görbe által bezárt síkrész területe, a görbe ívhossza, az x tengely körüli megforgatásával keletkező forgástest felszíne és térfogata.

65. Számítsa ki az görbe első pozitív félhulláma alatti területet, súlypontjának koordinátáit és az x tengely körüli forgatásával nyert forgástest térfogatát!

66. Számítsa ki az függvény görbéjének ívhosszát a [8;16] intervallumon.

67. Számítsa ki az alábbi görbék által határolt síkrészek területét és adja súlypontjaik helyét:

a.) , b.) ,

68. Számítsa ki az alábbi improprius integrálokat:

a.) , b.) , c.), d.) .