Házi megbeszélése
1. feladat
| > |
l:=[]:x:=1:
while x<10^6 do
l:=[op(l),x];
x:=x*2;
end do:
l; |
![[1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048, 4096, 8192, 16384, 32768, 65536, 131072, 262144, 524288]](images/4ora_1.gif)
Egy kicsit egyszerűbb megoldás, nem halmazzal, hanem csak kiíratással:
| > |
x:=1:
while x<10^6 do
print(x);
x:=x*2;
end do: |




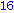
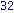
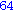
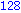
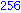
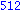
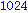
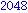
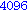
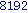
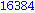
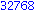
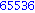
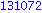
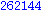
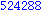
Illetve:

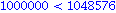
Ezért:
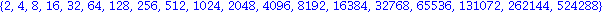
2. feladat
| > |
[seq(3^n mod 39,n=1..4)]; |
![[3, 9, 27, 3]](images/4ora_25.gif)
Körbeért, ezért a maradékok
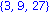
Tökéletees, ha valaki 0-tól indította:
| > |
{seq(3^n mod 39,n=0..3)}; |
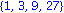
3. feladat
Persze jobban örülnék a listás megoldásnak, de még ez is jó.
| > |
for i from 1 to 1000 do
if i mod 7 = 4 and i mod 3 =2
then
print( i );
end if;
end do; |
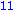
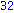
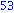
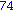
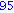
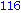
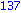
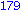
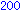
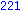
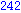
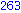
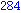
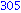
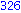
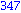
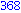
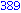
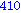
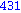
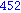
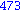
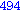
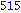
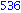
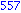
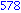
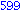
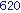
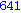
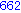
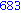
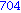
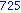
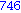
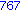
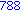
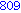
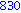
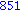
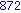
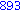
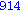
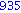
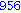
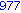
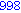
Illetve tanuljunk újat: a select parancs első paramétere egy igazzal (true-val) vagy hamissal (false-szal) visszatérő függvény, második paramétere egy lista. Csak azon elemeket hagyja meg a listában, amelyekre a megadott függvény igazzal tér vissza.
| > |
select(x -> if x mod 7 = 4 and x mod 3 = 2 then true; else false; end if, [seq(i,i=1..1000)]); |
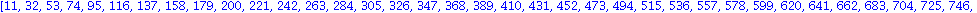

4. feladat
Az előző megoldások bármelyike jó, sőt még egyszerűbben is lehet. Nem íratom ki, sok van, csak 1000-ig:
| > |
select(x -> isprime(x) and isprime(x+2), [seq(i,i=1..1000)]); |
![[3, 5, 11, 17, 29, 41, 59, 71, 101, 107, 137, 149, 179, 191, 197, 227, 239, 269, 281, 311, 347, 419, 431, 461, 521, 569, 599, 617, 641, 659, 809, 821, 827, 857, 881]](images/4ora_78.gif)
5. feladat
| > |
n:=1:
while n! < 11^n do
n:=n+1;
od:
n; |
Pár plusz trükk
A select-eket lehet egymásba ágyazni.
| > |
select(i -> isprime(i) and isprime(i+2), select(k -> k mod 2 = 1, [seq(2
* k + 1, k=1..10^3 / 2 - 1)])); |
![[3, 5, 11, 17, 29, 41, 59, 71, 101, 107, 137, 149, 179, 191, 197, 227, 239, 269, 281, 311, 347, 419, 431, 461, 521, 569, 599, 617, 641, 659, 809, 821, 827, 857, 881]](images/4ora_80.gif)
Ami csak a páratlanokat nézi és nem néz meg kétszer minden prímet, hogy az-e (ami ugye drága művelet):
| > |
p0:=false:
n:=3:
l:=[]:
while n < 10^3 do
p:=isprime(n):
if (p and p0) then l:=[op(l), n-2]: fi:
p0 := p:
n := n+2:
od:
l ; |
![[3, 5, 11, 17, 29, 41, 59, 71, 101, 107, 137, 149, 179, 191, 197, 227, 239, 269, 281, 311, 347, 419, 431, 461, 521, 569, 599, 617, 641, 659, 809, 821, 827, 857, 881]](images/4ora_81.gif)
Műveletek mátrixokkal
Mátrix-okról még nem tanultatok túl sokat, így ez egy plusz rész. A későbbiekben még jól jöhet.
Betöltjük a lineáris algebrával foglalkozó csomagot.
Létrehozunk egy mátrix-ot.
| > |
A:=<<1,2,3>|<3,4,5>|<1,3,10>>; |
![A := Matrix([[1, 3, 1], [2, 4, 3], [3, 5, 10]])](images/4ora_93.gif)
![Matrix([[(-5)/2, 5/2, (-1)/2], [11/10, (-7)/10, 1/10], [1/5, (-2)/5, 1/5]])](images/4ora_94.gif)
| > |
B:=Matrix([[1,2],[3,a]]); |
![B := Matrix([[1, 2], [3, a]])](images/4ora_95.gif)
| > |
matrix(3,3,[2,3,6,3,3,6,6,6,6]); |
![matrix([[2, 3, 6], [3, 3, 6], [6, 6, 6]])](images/4ora_96.gif)
A B mátrix-ot négyzetre emeljük.
![Matrix([[7, 2+2*a], [3+3*a, 6+a^2]])](images/4ora_97.gif)
A B mátrix k-adik hatványa:
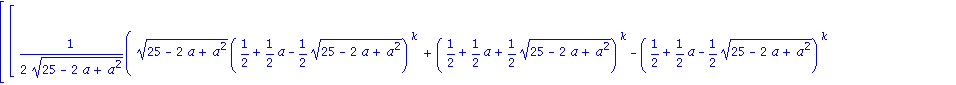
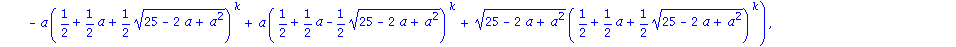
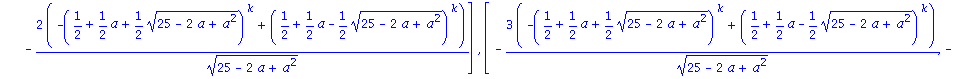
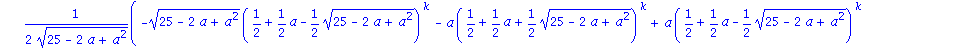
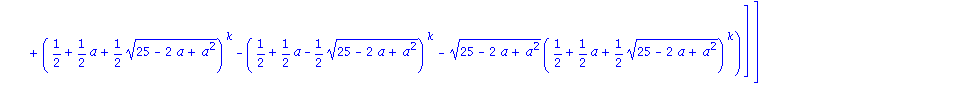
![Matrix([[1/66*(33^(1/2)*(5/2-1/2*33^(1/2))^5-3*(5/2+1/2*33^(1/2))^5+3*(5/2-1/2*33^(1/2))^5+33^(1/2)*(5/2+1/2*33^(1/2))^5)*33^(1/2), -2/33*(-(5/2+1/2*33^(1/2))^5+(5/2-1/2*33^(1/2))^5)*33^(1/2)], [-1/11...](images/4ora_103.gif)
![Matrix([[1/66*(33^(1/2)*(5/2-1/2*33^(1/2))^5-3*(5/2+1/2*33^(1/2))^5+3*(5/2-1/2*33^(1/2))^5+33^(1/2)*(5/2+1/2*33^(1/2))^5)*33^(1/2), -2/33*(-(5/2+1/2*33^(1/2))^5+(5/2-1/2*33^(1/2))^5)*33^(1/2)], [-1/11...](images/4ora_104.gif)
Transzponált:
![Matrix([[1, 3], [2, a]])](images/4ora_105.gif)

![Matrix([[a/(-6+a), -2/(-6+a)], [-3/(-6+a), 1/(-6+a)]])](images/4ora_107.gif)
![A := Matrix([[1, 4], [2, 5]])](images/4ora_108.gif)

Mátrix-ok szorzata:
![matrix([[13, 2+4*a], [17, 4+5*a]])](images/4ora_110.gif)
A mátrix elemeit így érjük el. Módosíthatjuk is őket.
![A[1, 2] := 5](images/4ora_111.gif)
![Matrix([[1, 5], [2, 5]])](images/4ora_112.gif)
![matrix([[16, 2+5*a], [17, 4+5*a]])](images/4ora_113.gif)
![matrix([[19, 17+5*a], [23, 19+5*a]])](images/4ora_114.gif)
](images/4ora_115.gif)
![vector([110, 120])](images/4ora_116.gif)
], [3-14^(1/2)]])](images/4ora_117.gif)
], [3-14^(1/2)]]), Matrix([[5/(2+14^(1/2)), 5/(2-14^(1/2))], [1, 1]])](images/4ora_118.gif)
Plot
A plots csomag betöltése után sokkal több függvényt használhatunk rajzolásra.

Minden paraméter nélkül a plot megpróbálja intelligensen kirajzolni a függvényt. Ez nem mindig a legjobb.
| > |
plot(tan(x),x=-2*Pi..2*Pi); |
![[Plot]](images/4ora_124.gif)
A view paraméterrel adjuk meg a megjelenítendő téglalap sarkait, a discont=true hatására nem köti össze a szomszédos pontokat (így nem lesz egy függőleges egyenes a szakadási pontokban).
| > |
plot(tan(x),x=-2*Pi..2*Pi,view=[-2*Pi..2*Pi,-3..3],discont=true); |
![[Plot]](images/4ora_125.gif)
A contourplot a megadott függvény szintvonalait ábrázolja.
| > |
contourplot(sin(x*y),x=-3..3,y=-3..3); |
![[Plot]](images/4ora_126.gif)
Ugyanez 3d-ben:
| > |
contourplot3d(exp(-(2*x^2+y^2)/2),x=-2..2,y=-2..2); |
![[Plot]](images/4ora_127.gif)
A plot3d két paraméterrel dolgozik. A megadott függvény mondja meg, hogy az adott (x,y) pontban milyen magas legyen a pont. Minden rajzolás paraméterezhető, pl. ebben az esetben így értük el, hogy a szín is függjön a paraméterektől, és legye az ábrának neve.
| > |
plot3d(0.3*x^3-x+y^2, x=-2..2, y=-2..2, axes=box, color=0.3*x^3-x+y^2, title=Köbös); |
![[Plot]](images/4ora_128.gif)
A lehetséges opciók listája: a plot3d leírásában alul kattintsunk a plot3d[options] -ra,
vagy egyből menjünk a plot3d[options]-ra
Programozás
Legnagyobb közös osztó
Az alábbi függvény euklideszi algoritmussal számol legnagyobb közös osztót. A bemenő a és b paraméter után ::integer áll, amely hatására a bemenő paraméternek csak egész számot fogad el. Enélkül a programunk lefutna sajatgcd(Pi,"abc") bemenetre is, és valószínűleg csak a mod-nál futna le.
Egy függvény visszatérési értéke az utolsó számolt képlet eredménye, vagy a return parancs után megadott rész. A return használata esetén azonnal megszakad a program futása, és a megadott értékkel tér vissza.
| > |
sajatgcd:=proc(a::integer, b::integer)
if b=0
then a;
else sajatgcd(b,a mod b);
end if;
end proc; |


Fibonacci
Fibonacci sorozat n. tagját kiszámoló eljárás. Rekurzívan oldjuk meg. Ha n >= 3, akkor meghívjuk a fib függvényt az n-1 és n-2 helyen, és ennek összegével térünk vissza. Az option remember segítségével megjegyzi a már kiszámolt értékeket, így lényegesen gyorsabb lesz a program. Így lineáris lesz a futási idő, enélkül pedig exponenciális.
| > |
fib:=proc(n::integer)
option remember;
if n < 3 then return 1; fi;
fib(n-1)+fib(n-2);
end proc; |

Más megoldás rekurzív hívás nélkül:
| > |
fibi := proc(n::integer)
local n0, a, b, r:
a := 1: b := 1: r := 1: n0 := 2:
while n0 < n do
r := a + b:
b := a:
a := r:
n0 := n0 + 1:
od:
r;
end; |

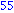
Áttérés kettes számrendszerre
A bemenő paramétert szeretnék kettes számrendszerre váltani. Például 6-ra [1,1,0]-t szeretnénk kapni, mert 4*1+2*1+1*0 = 6. A legnagyobb kettőhatvány, amely még nem nagyobb 6-nál, az a 4. 4-et úgy tudjuk kifejezni 6-tal, hogy 4=2^floor(log(6)/log(2)), ahol a floor az alsó egészet jelenti. Ezután minden lépésben levonjuk a megmaradó számból az épp vizsgált 2-hatványt ha tudjuk, ekkor egy 1-est teszünk az r lista végére, egyébként 0-t. Majd felezzük a 2-hatványunkat. Az elején van egy nn változó, amit utána át is másolunk n-re. Így nem az nn-et írjuk felül a munkánk során.
A local után fel kell sorolni minden használt, nem paraméterként kapott változót.
| > |
kettes:=proc(nn::integer)
local r,x,n;
r:=[];
n:=nn;
x:=2^floor(log(n)/log(2));
while(x>=1) do
if n >= x
then
r := [op(r),1]; n := n-x;
else
r := [op(r),0];
end if;
x := x/2;
end do:
r;
end proc; |
![kettes := proc (nn::integer) local r, x, n; r := []; n := nn; x := 2^floor(log(n)/log(2)); while 1 <= x do if x <= n then r := [op(r), 1]; n := n-x else r := [op(r), 0] end if; x := 1/2*x end do; r en...](images/4ora_136.gif)
![kettes := proc (nn::integer) local r, x, n; r := []; n := nn; x := 2^floor(log(n)/log(2)); while 1 <= x do if x <= n then r := [op(r), 1]; n := n-x else r := [op(r), 0] end if; x := 1/2*x end do; r en...](images/4ora_137.gif)
![kettes := proc (nn::integer) local r, x, n; r := []; n := nn; x := 2^floor(log(n)/log(2)); while 1 <= x do if x <= n then r := [op(r), 1]; n := n-x else r := [op(r), 0] end if; x := 1/2*x end do; r en...](images/4ora_138.gif)
![kettes := proc (nn::integer) local r, x, n; r := []; n := nn; x := 2^floor(log(n)/log(2)); while 1 <= x do if x <= n then r := [op(r), 1]; n := n-x else r := [op(r), 0] end if; x := 1/2*x end do; r en...](images/4ora_139.gif)
![kettes := proc (nn::integer) local r, x, n; r := []; n := nn; x := 2^floor(log(n)/log(2)); while 1 <= x do if x <= n then r := [op(r), 1]; n := n-x else r := [op(r), 0] end if; x := 1/2*x end do; r en...](images/4ora_140.gif)
![[1, 0]](images/4ora_141.gif)
![[1]](images/4ora_142.gif)
![[1, 1, 0]](images/4ora_143.gif)
![[1, 1, 1]](images/4ora_144.gif)
![[1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]](images/4ora_145.gif)
Leghosszabb tiszta fejsorozat
Vegyünk 100 hosszú egy listát, amelyben 0-ák és 1-esek vannak. Hogy ne nekünk kelljen ilyet írni, csinálhatunk ilyet véletlenszerűen:
| > |
l:=[seq(rand() mod 2,i=1..100)]; |
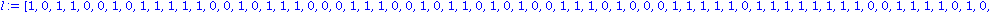

Számoljuk meg első körben, hogy hány 1-es van benne.
| > |
s:=0:
for i from 1 to nops(l) do
if l[i]=1 then
s := s+1;
end if;
end do;
s; |
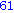
Ha az 1-est fejnek, a 0-t pedig írásnak vesszük, akkor megszámolhatjuk a leghosszabb tiszta (egymás után jövő) fejsorozat hosszát. A k változóban tároljuk az éppen addig talált leghosszabb sorozat hosszát, és az m-ben tároljuk a maximumát a k értékeknek.
| > |
m:=0:
k:=0:
for i from 1 to nops(l) do
if l[i]=1 then
k:=k+1;
else
k:=0;
end if;
m:=max(m,k);
end do:
m;
|

Ugyanezt írjuk meg függvényben. Az előny az, hogy ezután könnyen meg tudjuk hívni többször.
| > |
tiszta:=proc(n::integer)
local l,i,k,m;
l:=[seq(rand() mod 2,i=1..n)];
m:=0:
k:=0:
for i from 1 to n do
if l[i]=1 then
k:=k+1;
else
k:=0;
end if;
m:=max(m,k);
end do;
m;
end proc; |
![tiszta := proc (n::integer) local l, i, k, m; l := [seq(`mod`(rand(), 2), i = (1 .. n))]; m := 0; k := 0; for i to n do if l[i] = 1 then k := k+1 else k := 0 end if; m := max(m, k) end do; m end proc](images/4ora_150.gif)
![tiszta := proc (n::integer) local l, i, k, m; l := [seq(`mod`(rand(), 2), i = (1 .. n))]; m := 0; k := 0; for i to n do if l[i] = 1 then k := k+1 else k := 0 end if; m := max(m, k) end do; m end proc](images/4ora_151.gif)
![tiszta := proc (n::integer) local l, i, k, m; l := [seq(`mod`(rand(), 2), i = (1 .. n))]; m := 0; k := 0; for i to n do if l[i] = 1 then k := k+1 else k := 0 end if; m := max(m, k) end do; m end proc](images/4ora_152.gif)
![tiszta := proc (n::integer) local l, i, k, m; l := [seq(`mod`(rand(), 2), i = (1 .. n))]; m := 0; k := 0; for i to n do if l[i] = 1 then k := k+1 else k := 0 end if; m := max(m, k) end do; m end proc](images/4ora_153.gif)
![tiszta := proc (n::integer) local l, i, k, m; l := [seq(`mod`(rand(), 2), i = (1 .. n))]; m := 0; k := 0; for i to n do if l[i] = 1 then k := k+1 else k := 0 end if; m := max(m, k) end do; m end proc](images/4ora_154.gif)

Warning, the name changecoords has been redefined
Az ábrát elnézve: az esetek többségében 5-6-7-8 tiszta fejsorozat a leggyakoribb.
| > |
listplot(sort( [seq(tiszta(100),i=1..1000)] )); |
![[Plot]](images/4ora_157.gif)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![A := Matrix([[1, 3, 1], [2, 4, 3], [3, 5, 10]])](images/4ora_93.gif)
![Matrix([[(-5)/2, 5/2, (-1)/2], [11/10, (-7)/10, 1/10], [1/5, (-2)/5, 1/5]])](images/4ora_94.gif)
![matrix([[2, 3, 6], [3, 3, 6], [6, 6, 6]])](images/4ora_96.gif)
![Matrix([[7, 2+2*a], [3+3*a, 6+a^2]])](images/4ora_97.gif)
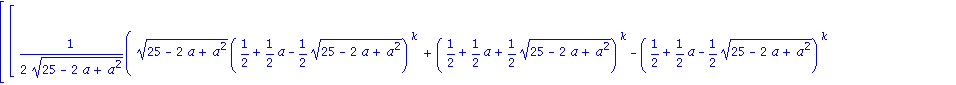
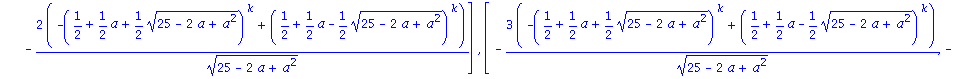
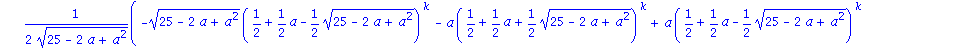
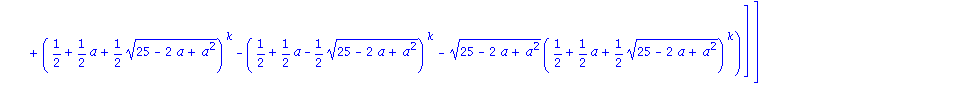
![Matrix([[1/66*(33^(1/2)*(5/2-1/2*33^(1/2))^5-3*(5/2+1/2*33^(1/2))^5+3*(5/2-1/2*33^(1/2))^5+33^(1/2)*(5/2+1/2*33^(1/2))^5)*33^(1/2), -2/33*(-(5/2+1/2*33^(1/2))^5+(5/2-1/2*33^(1/2))^5)*33^(1/2)], [-1/11...](images/4ora_103.gif)
![Matrix([[1/66*(33^(1/2)*(5/2-1/2*33^(1/2))^5-3*(5/2+1/2*33^(1/2))^5+3*(5/2-1/2*33^(1/2))^5+33^(1/2)*(5/2+1/2*33^(1/2))^5)*33^(1/2), -2/33*(-(5/2+1/2*33^(1/2))^5+(5/2-1/2*33^(1/2))^5)*33^(1/2)], [-1/11...](images/4ora_104.gif)
![Matrix([[a/(-6+a), -2/(-6+a)], [-3/(-6+a), 1/(-6+a)]])](images/4ora_107.gif)
], [3-14^(1/2)]])](images/4ora_117.gif)
], [3-14^(1/2)]]), Matrix([[5/(2+14^(1/2)), 5/(2-14^(1/2))], [1, 1]])](images/4ora_118.gif)
![[Plot]](images/4ora_124.gif)
![[Plot]](images/4ora_125.gif)
![[Plot]](images/4ora_126.gif)
![[Plot]](images/4ora_127.gif)
![[Plot]](images/4ora_128.gif)
![[Plot]](images/4ora_157.gif)