jsMath

Sage kalkulus

Sage kalkulus

Alapértelmezés szerint x Sage változó:
x 
        
x

Ez nem mondható el a többi betűről:
y 
        
Traceback (click to the left of this block for traceback)
...
NameError: name 'y' is not defined

Oldjuk meg az y^2 == 9 egyenletet.

Solve használata:

solve(megoldandó egyenlet vagy egyneletek, kifejezendő változó vagy változók)
solve(y^2==9,y) 
        
Traceback (click to the left of this block for traceback)
...
NameError: name 'y' is not defined

Ezentúl kezelje y-t is változóként:
var('y') 
        
y
solve(y^2==9,y) 
        
[y == -3, y == 3]
solve(e^y==2,y) 
        
[y == log(2)]
var('a b c') 
        
(a, b, c)
solve(a*x^2+b*x+c==0,x) 
        
[x == -1/2*(b + sqrt(-4*a*c + b^2))/a, x == -1/2*(b - sqrt(-4*a*c +
b^2))/a]

Több egyenlet esetén használjunk listát:
solve([x+y^2==2, x-y^2==-2],[x,y]) 
        
[[x == 0, y == -sqrt(2)], [x == 0, y == sqrt(2)]]

Egyenletet is menthetünk változóba:
eq1 = x^2+y^2 == 10 
       
eq2 = x+2*y==0 
       
solve([eq1,eq2],[x,y]) 
       

Függvények:
f(x) = 2*sin(x/2) 
       
f(3) 
        
2*sin(3/2)
f 
        
x |--> 2*sin(1/2*x)
diff(f,0) 
        
x |--> 2*sin(1/2*x)
g(x,y)=x^2+y 
       
g(10,1) 
        
101
g 
        
(x, y) |--> x^2 + y
diff(g,x) 
        
(x, y) |--> 2*x
diff(g,y) 
        
(x, y) |--> 1

Egyszerűsítések:
q = sin(x)^2 + cos(x)^2 
       
q.full_simplify() 
        
1
p = (x-2)^3/2-6*x^2-1 
       
p.full_simplify() 
        
1/2*x^3 - 9*x^2 + 6*x - 5

Gyökök:
p.roots() 
        
[(-1/2*(sqrt(1457) + 185)^(1/3)*(I*sqrt(3) + 1) + (16*I*sqrt(3) -
16)/(sqrt(1457) + 185)^(1/3) + 6, 1), (-1/2*(sqrt(1457) +
185)^(1/3)*(-I*sqrt(3) + 1) + (-16*I*sqrt(3) - 16)/(sqrt(1457) +
185)^(1/3) + 6, 1), ((sqrt(1457) + 185)^(1/3) + 32/(sqrt(1457) +
185)^(1/3) + 6, 1)]

p gyökei közelítőleg (a CC itt a komplex számokat jelenti):
p.roots(ring=CC) 
        
[(0.329368774254962 - 0.684233509252514*I, 1), (0.329368774254962 +
0.684233509252514*I, 1), (17.3412624514901 - 2.22044604925031e-16*I,
1)]
p.roots(ring=ComplexField(200)) 
        
[(17.341262451490075624610186683084137128506630479155442147265, 1),
(0.32936877425496218769490665845793143574668476042227892636758 -
0.68423350925251386013249896992572249387013850705381221364044*I, 1),
(0.32936877425496218769490665845793143574668476042227892636758 +
0.68423350925251386013249896992572249387013850705381221364044*I, 1)]

A polinomnak a valós számok között csak 1 gyöke van:
p.roots(ring=RR) 
        
[(17.3412624514901, 1)]
RR 
        
Real Field with 53 bits of precision
CC 
        
Complex Field with 53 bits of precision

Helyettesítés:
p.subs(x=5) 
        
-275/2
p(x=5) 
        
-275/2
abs( p(x=5) ) 
        
275/2
p(x=5).abs() 
        
275/2
p(x=oo) 
        
-Infinity
(x+10)(x=2) 
        
12

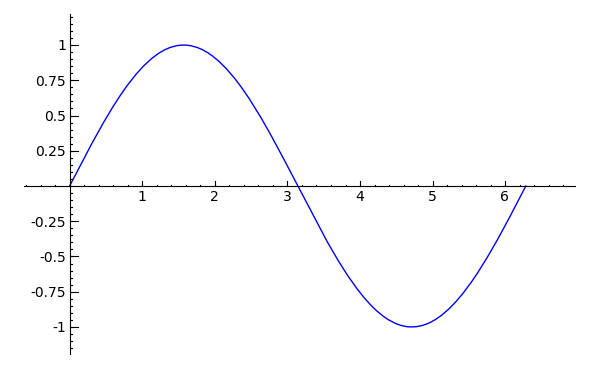
Rajzolás plot függvénnyel:

plot( rajzolandó függvény, változó, mettől, meddig )
plot(sin(x),x,0,2*pi) 
       

A plot valójában egy objektumot hoz létre, így a plot parancs nem rajzol feltétlen (nem olyan, mint a print). A show mindenképp rajzol.
plot(sin(x),x,0,2*pi) 1+1 
        
2
P = plot(sin(x),x,0,2*pi) Q = plot(cos(x),x,0, pi,color=(1,0,0)) 
       
P+Q 
       
sum([P,Q]) 
       

A show paraméterei között a figsize értékeit 2 elemű turple-ben vagy listában kell megad, ahol a kivánt pixelméret századát kell írni mindkét koordinátában.
show(P+Q,figsize=(6,2),xmin=0,xmax=2,ymin=-1,ymax=2) 1+1 
        

2
sum([ plot(sin(k*x),(x,0,2*pi)) for k in [1,1.5..5] ]) 
       
plot(sin(x),(x,0,2*pi),color=(1,0,1)) 
       
sum([ plot(sin(k*x),(x,0,2*pi),color=(k/7,k/7,1)) for k in [1,1.5..5] ]) 
       
P+line([ [-2,-2], [2,2] ])+text("Behuztuk az erintot 0-ban",[4,2],rgbcolor=(1,0,0)) 
       
sum( [ point( [cos(t), sin(t), t]) for t in [0,0.1,..10] ]) 
       
You do not have the
Java Runtime Environment
installed for applet support.
Visit www.java.com
 Get Image
 
       

A show parancs a képleteket is szebben ábrázolja:
show(p) 
        
21(x−2)3−6x2−1
show([1,2/3]) 
        
[1,32] 
show(1/(1+x/(1+1/y))) 
        
1x(y1+1)+1

A pretty_print általában szebb, ám nem minden esetben olvasható.

A pretty_print általában szebb, ám mintha kevesebb dolgot tudna megjeleníteni.
pretty_print(p) 
        
21(x−2)3−6x2−1
pretty_print([1,2/3]) 
        
[1,32] 
pretty_print(1/(1+x/(1+1/y))) 
        
1x(y1+1)+1
list_plot( [i for i in [1..100] if is_prime(i)] ) 
       
koord=[ [cos(t),sin(t)] for t in [0,0.5,..,2*pi]] koord 
        
[[1, 0], [0.877582561890373, 0.479425538604203], [0.540302305868140,
0.841470984807897], [0.0707372016677029, 0.997494986604054],
[-0.416146836547142, 0.909297426825682], [-0.801143615546934,
0.598472144103957], [-0.989992496600445, 0.141120008059867],
[-0.936456687290796, -0.350783227689620], [-0.653643620863612,
-0.756802495307928], [-0.210795799430780, -0.977530117665097],
[0.283662185463226, -0.958924274663138], [0.708669774291260,
-0.705540325570392], [0.960170286650366, -0.279415498198926]]
list_plot( koord ) 
       
var('x,y'); plot3d(sin(x-y)*y*cos(x),(x,-3,3),(y,-3,3)) 
       
You do not have the
Java Runtime Environment
installed for applet support.
Visit www.java.com
 Get Image

Tizedes törtek:
sqrt(2) 
        
sqrt(2)
show(sqrt(2)) 
        
√2 
n(sqrt(2)) 
        
1.41421356237310
sqrt(2).n() 
        
1.41421356237310
sqrt(2).n(digits=100) 
        
1.414213562373095048801688724209698078569671875376948073176679737990\
732478462107038850387534327641573
n(pi,digits=100) 
        
3.141592653589793238462643383279502884197169399375105820974944592307\
816406286208998628034825342117068
n(e) 
        
2.71828182845905
n(I) 
        
1.00000000000000*I

Differenciállás, határérték:
diff(p*sin(x),x) 
        
Traceback (click to the left of this block for traceback)
...
TypeError: argument symb must be a symbol

3-szor deriválunk x szerint:
diff(p*sin(x),x,3) 
        
9*(x - 6)*cos(x) - 9/2*((x - 2)^2 - 8*x)*sin(x) - 1/2*((x - 2)^3 -
12*x^2 - 2)*cos(x) + 3*sin(x)
diff(x^y+x^2/y,x,x,y) 
        
(y - 1)*y*x^(y - 2)*log(x) + (y - 1)*x^(y - 2) + y*x^(y - 2) - 2/y^2
limit(sin(x)/x,x=0) 
        
1
limit( (1+1/x)^x, x=infinity ) 
        
e
n(e) 
        
2.71828182845905
2+3*I 
        
3*I + 2
1/(2+3*I) 
        
-3/13*I + 2/13
abs(2+3*I) 
        
sqrt(13)
real(2+3*I) 
        
2
imag(2+3*I) 
        
3