Vektoros feladatok koordináták nélkül

Sok hallgatónál egyfajta berögzült szokás, hogy egy geometriai feladatnál, mintegy első lépésként, a problémát (egy ortonormált bázis fölvételével) egyből "koordinátatérbe" (esetünkben R³ -ba) helyezi át. Azonban fontos, hogy kialakuljon a megfelelő absztrakt szemlélet is; a vektorok koordináták nélkül is vektorok. Számtalan feladatban a koordinátázás inkább bonyolít, mint segít. Íme egy egyszerű, de szép példa.

---

Feladat: bizonyítsuk be, hogy nem adható meg úgy egy 4 (nemnulla) vektorból álló gyűjtemény, melyben bármely kettő közötti szög nagyobb mint 120°.

Megoldás: tegyük föl (indirekten), hogy v₁, v₂, v₃ és v₄ egy ilyen rendszert alkot. Nyílván azt is föltehetjük, hogy ezek a vektorok mind egység hosszúak (ha eredetileg nem is lettek volna azok, akkor is lenormálhattuk volna őket - ez a közöttük lévő szögeken nem változtat). Ekkor v_j· v_j = ||v_j||² = 1, míg j≠k esetén, mivel a cos a 0° és 180° közötti tartományon monoton csökken, v_j·v_k = a v_j és v_k által bezárt szög koszinusza ≤ cos(120°) ≤ -1/2. Így a szorzatot kifejtve

(v₁ + v₂ + v₃ + v₄)·(v₁ + v₂ + v₃ + v₄) ≤ 4 + 4*3*(-1/2) = -2,

ami ellentmondás; amit fölírtunk, az az összegvektor hossznégyzete, ami nem lehet negatív.

---

A fönti példában koordináták fölvételével annyi új változót hozunk be, hogy a feladat teljesen átláthatatlanná válik. Szintén jó geometriai példa ennek a gyakorlati feladatsornak az I/4 -es feladata, mellyel - nem mellesleg - pontosan úgy lehet elbánni, mint a minta-zh kérdéses utolsó geometriai feladatával, melynek akkor most következzen a megoldása.

A minta-zh 6. feladatának megoldása

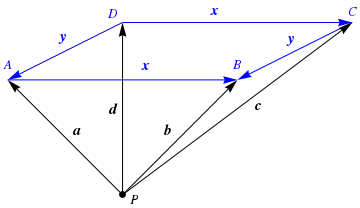
Az ilyen feladatoknál az első lépés, hogy egy ábrát készítünk, és az azon szereplő dolgokra (például pontokra és vektorokra) jelöléseket vezetünk be. Ez igen fontos - e nélkül később nem tudunk rájuk hivatkozni, tehát például nem tudunk velük kapcsolatban egyenleteket sem fölírni. Itt most a rombusz (kék szín) csúcsait A,B,C,D -nek, a kérdéses ismeretlen pontot pedig P -nek neveztük el. A P pontból a négy csúcsba mutató vektor - értelemszerűen - az a, b,c, d nevet kapta, a rombusz élvektorai x és y lettek.

A feladat szövege szerint ||x||2 = ||y||2 = ||a||2 = ||b||2 = 1, ||c||2 = 5/2, és ||d||2 = 3/2. A kérdés az x és y által bezárt α szög koszinusza, ami - mivel egység hosszú vektorokról van szó - éppen az x·y skaláris szorzat értéke. Ennek kiszámolásához egyenleteket fogunk fölírni. Nyilvánvaló, hogy az ábrán szereplő vektorok nem függetlenek. Például a P pontból kiindulva, először a d aztán pedig az y vektorral lépve ugyanúgy az A pontba jutunk, mintha csak az a vektor szerint mozdultunk volna el; tehát d + y = a. Ilyesmi megfontolások alapján számtalan vektoregyenletet tudunk fölírni, nekünk azonban most csak a következő háromra lesz szükségünk: i)     x + y = - d + b, ii)    d + x = c, iii)   b - x = a. Az első egyenlet alapján x·(x + y) = x·(-d + b) = - x·d + x·b, amiből is - tekintve, hogy x·(x + y) = x·x + x·y, és persze x·x = ||x||^2 = 1, a kérdéses skaláris szorzat x·y = -1 - x·d + x·b. A második egyenlet mindkét oldalát önmagával skalárisan szorozva (azaz mindkét oldal hossznégyzetét nézve): ||d||2 + 2 x·d + ||x||2 = ||c||2       ⇒       x·d = (1/2)(5/2 - 3/2 - 1) = 0, míg a harmadik egyenletből, a föntihez hasonló módszerrel ||b||2 - 2 x·b + ||b||2 = ||a||2       ⇒       x·b = (1/2)(1 + 1 - 1) = 1/2. Összetéve a kapottakat, cos(α) = x·y = -1 - 0 + 1/2 = -1/2 (azaz x és y 120° fokot zárnak be) és a rombusz területe T = ||x|| ||y || |sin(α)| = ||x|| ||y || √ 1-sin2(α)   = √ 3 /2.