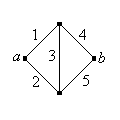
Adjuk meg az alábbi Wheatstone híd hálózatának megbízhatóságát (a névadó Charles Wheatstone)
A Bernoulli kísérlet folyamat, melynek névadója Jacob Bernoulli a valószínűségszámítás egyik legegyszerűbb, de egyben egyik legfontosabb véletlen kísérlet folyamata is. Lényegében a folyamat az érmefeldobás matematikai absztrakciója, de széleskörű alkalmazhatóságának következtében megállapodunk abban, hogy kielégíti a következő feltételeket:
Matematikailag a Bernoulli kísérleteket egy valszínűségi változó indikátor sorozatának tekintjük:
Egy indikátor változó egy valószínűségi változó, amely csak az 1 vagy 0 értéket veszi fel aszerint, hogy a kísérlet sikeres, vagy nem sikeres. Az indikátor változó egyszerűen a -edik kísérlet kimenetelének az eredménye. Így az indikátor változók függetlenek és ugyanolyan eloszlású sűrűségfüggvénnyel rendelkeznek:
Az ezen sűrűségfüggvény által definiált eloszlás Bernoulli eloszlás néven ismeretes. Statisztikai értelemben a Bernoulli kísérletek a Benoulli eloszlásból vett mintának felelnek meg. Speciálisan, az első kísérlet a Bernoulli eloszlásból vett elemű véletlen mintát alkot. Megjegyezzük, hogy a Bernoulli kísérletek egy paraméterrel, a valószínűséggel jellemezhetők.
Felhasználva az alapfeltevéseket mutassuk meg, hogy az első kísérlet sűrűségfüggvénye az alábbi módon adható meg
Feltételezve, hogy egy paraméterű Bernoulli kísérlet, mutassuk meg, hogy egy paraméterű Bernoulli kísérlet.
Tételezzük fel, hogy független valószínűségi változóknak egy sorozata, mindegyik egyenletes eloszlású a intervallumon. és , esetén legyen az esemény indikátor változója. Mutassuk meg, hogy paraméterű Bernoulli kísérlet.
Megjegyezzük, hogy az előző gyakorlatban a Bernoulli kísérletek a paraméter minden lehetséges értéke esetén egy közös valószínűségi téren vannak definiálva. A konstrukció ezen típusára néha mint összekapcsolt kísérletekre hivatkozunk. Ez a gyakorlat azt is mutatja, hogyan szimuláljuk a Benoulli kísérleteket véletlen számok segítségével. Az összes többi véletlen kísérlet (folyamat), amit ebben a fejezetben tanulmányozunk a Bernoulli kísérletsorozatnak a függvényei és ezért is tudjuk szimulálni.
A későbbi hivatkozásokhoz számítsuk ki a paraméterű általános indikátor változó várható értékét, varianciáját, és a valószínűség generáló függvényét.
Mutassuk meg, hogy
Mutassuk meg, hogy
Mutassuk meg, hogy .
Vázoljuk fel az 5. gyakorlatban a varianciát, mint függvényét. Figyeljük meg, hogy a variancia akkor a legnagyobb, amikor és akkor a legkisebb, amikor vagy .
Mint korábban megjegyeztük, a Bernoulli kísérletek egy kézenfekvő pédája a pénzérmekísérletek, ahol a síker jelenti a fej, a sikertelenség az írásdobást. A paraméter a fejdobás valószínűsége(így általában az érme nem szabályos.).
Az alap érmekísérletben legyen és . Végezzük el a kísérletet és figyeljük meg az eredményeket. Ismétlejük meg a kísérletet az alábbi értékekkel: .
Egy bizonyos értelemben a Bernoulli kísérletek legáltalánosabb példája akkor fordul elő, amikor egy kísérletet megismétlünk. Speciálisan tételezzük fel, hogy van egy alapkísérletünk és egy esemény érdekel minket. Tegyük fel, hogy egy összetett eseményt hozunk létre, ami az alapkísérlet független megismétléseiből áll. Azt mondjuk, hogy az -edik kísérlet sikeres, ha az esemény bekövetkezik az -edik ismétlésre és az -edik kísérlet sikertelen, ha az esemény nem következik be az -edik ismétlésre. Ez nyilvánvalóan egy Bernoulli kísérlet sorozatot definiál.
Bernoulli kísérleteket dichotom populációból is alkothatunk. Speciálisan tételezzük fel, hogy van egy populációnk, amelynek két típusú kimenetele van, amelyekre 0-val és 1-gyel hívatkozunk. Például lehet szó személyről aki vagy férfi vagy nő, vagy egy alkatrészről, ami vagy jó vagy hibás. Válasszunk ki objektumot véletlenszerűen a populációból; definíció szerint ez azt jelenti, hogy ha egyszerre (visszatevés nélkül) történik az elemek kiválasztása, akkor a populációban mindegyik objektum egyenlő valószínűséggel választható ki. Ha a mintavétel visszatevéssel történik, akkor mindegyik objektum a következő húzás elött visszakerül a kihúzandók közé. Ebben az esetben az egymás utáni húzások függetlenek, így a mintában lévő objektumok típusai paraméterű Bernoulli kísérleteknek egy sorozatát alkotják. Ez a paraméter a populációban lévő 1-es objektumtípusainak hányada. Ha a mintavétel visszatevés nélküli, akkor az egymás utáni húzások nem függetlenek, így a mintában lévő objektumok típusai nem alkotják Bernoulli kísérleteknek egy sorozatát. Azonban, ha a populáció mérete a mintavétel méretéhez viszonyítva nagy, a függőség elhanyagolható, így az összes gyakorlati tervben a mintában lévő objektumok típusai Bernoulli kísérletek sorozataként kezelhetők. További diszkussziók találhatók a dichotom populációból való mintavételről a Véges elemű mintamodellek c. fejezetben.
Tételezzük fel, hogy egy hallgató többválaszos tesztet tölt ki. A teszt 10 kérdésből áll, melyek mindegyikére 4 lehetséges válasz van (de csak 1 a helyes). Ha a hallgató vakon találgat mindegyik kérdésnél, meg tudjuk úgy csinálni a kérdéseket, hogy Bernoulli kísérletsorzatot kapjunk? Ha így áll a dolog, azonosítsuk a kísérlet kimeneteleit és a paramétert!
Az pályázó egy bizonyos körzetben indul a jelölésért. Húsz személyt kiválasztottak a szavazók közül véletlenszerűen és megkérdezték tőlük, vajon az személyre szavaznak-e. A válaszok alkothatnak-e Bernoulli kísérletsorozatot? Ha igen, azonosítsuk a kísérlet kimeneteleit és a paramétert!
Egy amerikai rulettben 38 vájat van; 18 piros, 18 fekete és 2 zöld. A játékos 15-ször rulettezik, minden egyes alkalommal a pirosra fogadva. A kimenetelek alkothatnak-e Bernoulli kísérletsorozatot? Ha igen, azonosítsuk a kísérlet kimeneteleit és a paramétert!
A Rulettet részletesebben a Szerencsejáték fejezetben elemezzük.
Két tenisz játékos 6 gémből álló meccset játszik. A kimenetelek alkothatnak-e Bernoulli kísérletsorozatot? Ha igen, azonosítsuk a kísérlet kimeneteleit és a paramétert!
Emlékeztetünk ara, hogy a szerkezeti megbízhatóság standard modelljében a rendszer komponensből áll, amelyek egymástól függetlenül működnek. Jelölje az -edik komponens állapotát, ahol 1 jelenti, hogy működik, 0 jelenti, hogy hibás a komponens. Ha a komponensek mindegyike ugyanolyan típúsú, akkor alapfeltevésünk, hogy az
állapot vektor Bernoulli kísérleteknek egy sorozata. A rendszer állapota (ismét 1 jelenti, hogy működik, 0 jelenti, hogy hibás a komponens) csak a komponensek állapotától függ és így egy valószínűségi változó
ahol a struktúra függvény. Általában annak valószínűsége, hogy az eszköz működik, az eszköz megbízhatósága, így a Bernoulli kísérletsorozat paramétere a komponensek közös megbízhatósága. A függetlenség miatt a rendszer megbízhatósága a komponens megbízhatóságnak egy függvénye:
ahol hangsúlyozzuk a paraméteren értelmezett valószínűségi mező függetlenségét. Általában elég, ha ezt a függvényt, mint megbízhatósági függvényt ismerjük. Rendszerint az a feladatunk, hogy megtaláljuk a megbízhatósági függvényt, és megtaláljuk a struktúrafüggvényt.
Emlékeztetünk arra, hogy egy soros rendszer akkor és csak akkor működik, ha mindegyik komponense működik.
Emlékeztetünk arra, hogy egy párhuzamos rendszer akkor és csak akkor működik, ha legalább az egyik komponense működik.
Emlékeztetünk arra, hogy néhány esetben a rendszert reprezentálhatjuk, mint egy gráfot vagy hálózatot. Az élek a komponenseket, a csúcsok a komponensek közötti kapcsolatokat reprezentálják. A rendszer akkor és csak akkor működik, ha létezik két kijelölt csúcs között működő útvonal, amelyeket -val és -vel jelölünk.
Tételezzük fel, hogy egy populációban minden személy, egymástól függetlenül valószínűséggel rendelkezik egy bizonyos betegséggel. Így, a betegséget illetően a populációban lévő személyek Bernoulli kísérletsorozatot alkotnak. A betegséget egy vérvizsgálattal lehet azonosítani, aminek természetesen költsége van.
Egy létszámú csoport ( ) esetén két stratégiát követhetünk. Az első szerint minden személyt megvizsgálunk egyenként, s ezért személyt kell vizsgálnunk, s így vérvizsgálatot kell végeznünk. A második stratégia szerint összegyűjtjük a személy vérmintáját és először együtt vizsgáljuk (egyetlen egy teszttel). Feltételezzük, hogy a teszt eredménye akkor és csak akkor negatív, ha a személy mindegyike egészséges. Ebben az esetben egy teszt elvégzése szükséges. Másrészről a teszt eredménye akkor és csak pozitív, ha legalább egy személy beteg, ekkor egyenként tesztelni kell a személyeket. Ennél a stratégiánál teszt végrehajtása szükséges. Jelölje az összegyüjtött stratégia esetén a szükséges tesztek számát.
Mutassuk meg, hogy
Mutassuk meg, hogy várható értékben megadva az összegyűjtött stratégia akkor és csak akkor jobb, mint az alapstratégia, ha
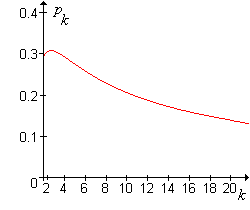
A kritikus érték ábráját, mint -nak a függvényét mutatja az alábbi ábra:
Mutassuk meg, hogy
A 18. gyakorlatból következik, hogy ha , akkor az összegyűjtésnek nincs értelme, tekintet nélkül a csoport méretére. A másik szélsőséges esetben, ha nagyon kicsi, a betegség igen ritka, az összegyűjtés jobb, kivéve, ha a csoportméret nagyon nagy.
Most tételezzük fel, hogy személyünk van. Ha akkor tudunk csinálni részpopulációkat, csoport van és mindegyik csoportban személy. Alkalmazzuk az összegyüjtött stratégiát mindegyik csoportra. Megjegyezzük, hogy megfelelel egyetlen egy tesztnek és megfelelel a teljes populációra vonatkozó összegyűjtött stratégiának. Jelölje az csoporthoz szükséges tesztek számát.
Bizonyítsik be, hogy függetlenek és mindegyikük a 16. gyakorlatban megadott eloszlással rendelkezik.
Az ehhez szükséges tesztek teljes számára az alábbi terv érvényes
Mutassuk meg, hogy a tesztek teljes számának várható értéke
Mutassuk meg, hogy a tesztek teljes számának varianciája
Így, a várható értékkel kapcsolatban az optimális stratégia a populáció felosztása darab fős csoportra, ahol a 20. gyakorlatban definiált függvényt minimalizálja. Igen nehéz optimális értékére zárt formulát adni, de ez az érték numerikusan meghatározható konkrét és értékekre.
és következő értékeire adjuk meg az optimális összegyűjtéshez a értéket és a tesztek várható számát. (Szorítkozzunk azon értékeire, amelyek osztják értékét!)
Ha
nem osztója
-nek, akkor az
személyből álló populációt
csoportra bontjuk
személyt téve mindegyik csoportba és a maradék
csoport
személyből áll. Ez nyilvánvalóan bonyolítja az elemzést, de nem vezet be új ötletet, így ennek az esetnek a vizsgálatát az érdeklődő olvasóra bízzuk.