A Bertrand féle probléma abból áll, hogy adjuk meg annak valószínűségét, hogy a körnek egy véletlen húrja
nem hosszabb, mint a körbe írt szabályos háromszögnek az oldala. A problémát Joseph Louis Bertrand tanulmányozta 1889-ben, ezért róla kapta a nevét.
Kiderül, hogy a Bertrand problémára legalább három válasz adható, attól függően, hogyan interpretáljuk a véletlen húr
kifejezést.
Az egyértelmű válasz hiányát ekkor paradoxonként kezelték, mivel azt feltételezték (naív módon, utólagos előrelátással), hogy csak egyetlen természetes válasz létezhet.
Végezzük el a Bertrand kísérletet 100-szor, minden kísérlet után frissítve a következő modellek mindegyikére. Ne törődjünk azzal, hogy mi a modellek jelentése, de lássuk a különbséget a kimenetelek viselkedésében.
Ahhoz, hogy matematikailag megfogalmazzuk a problémát, vegyük a kör középpontjának a pontot és a kör sugara legyen egységnyi. Ezek a feltevések nem befolyásolják a feladat általánosságát, mert a kör középpontjához való távolság és a kör sugara, mint hosszegység relatív. Vizsgáljunk egy húrt a körön. Feltehetjük, hogy a húr egyik végpontja és a másik végpontja , ahol Ekkor a következő adatok megadásával teljesen meghatároztuk a húr helyzetét:
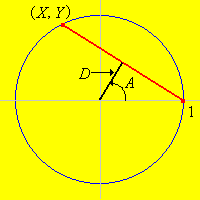
Mutassuk meg, hogy .
Mutassuk meg, hogy .
Mutassuk meg, hogy .
Mutassuk meg, hogy a 2. és 3. gyakorlat relációi megfordíthatók és adjuk meg az inverz relációkat!
Ha a húrt valószínűségelméleti módon generáljuk, akkor , , , és valószínűségi változók lesznek. Az 5. gyakorlat eredményének fényében, tehát ha a , , vagy változók bármelyikének megadjuk az eloszlását, az mind a négy változó eloszlását meghatározza.
Mutassuk meg, hogy a húr és a kör pontjában húzott érintő egyenesének a szögével egyezik meg!
Most vizsgáljuk az körbe írt egyenlőoldalú háromszöget olymódon, hogy a háromszög egyik csúcsa az pont. Vizsgáljuk azt a húrt, amelyet a háromszög felső oldala határoz meg.
Mutassuk meg, hogy ilyen húr esetén a szög, a távolság, és a koordináta változók az alábbi értékeket veszik fel:
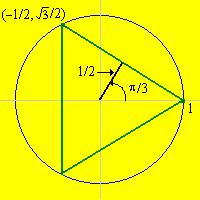
Tételezzük fel, hogy a húrt valószínűségelméleti úton választjuk.
Felhasználva a 7. gyakorlatot mutassuk meg, hogy a húr hossza akkor és csak akkor nagyobb, mint az egyenlőoldalú háromszög oldala, ha a következő ekvivalens feltételek teljesülnek:
Amikor egy dolgot véletlenszerűen
generálunk, az objektumot meghatározó természetes
változók sorozatának egyenletes eloszlásúnak kell lenni. A pénzérme középpontjának a koordinátái egy ilyen sorozatot alkotnak a Buffon féle pénzérme kísérletben; a szög és a távolságváltozók ilyen sorozatot alkotnak a Buffon féle tűkísérletben.
A Bertrand paradoxon nehézsége abban áll, hogy a
, távolság, az
, szög és az
koordináta mindegyike természetes változónak tűnik, hogy meghatározza a húrt, de különböző modelleket kapunk attól függően, hogy melyik határozza meg az egyenletes eloszlást.
Tételezzük fel, hogy egyenletes eloszlású a intervallumon.
Mutassuk meg, hogy a Bertrand paradoxon problémájának a megoldása:
A Bertrand kísérletben válasszuk az egyenletes távolság modellt. Végezzük el a kísérletet 1000-szer, 10-esével frissítve. Figyeljük meg a húr esemény relatív gyakoriság függvényének a valószínűséghez való nyilvánvaló konvergenciáját.
Használja fel a változók felcserélésének a formuláját, hogy megmutassa, hogy az (szög)változó sűrűségfüggvénye a következő
Használja fel, a változók felcserélésének formuláját, hogy megmutassa, hogy az változó sűrűségfüggvénye a következő
Megjegyezzük, hogy és nem egyenletes eloszlású.
Mutassuk meg, hogyan szimuláljuk a , , és változókat, felhasználva a véletlen számokat.
Tételezzük fel, hogy egyenletes eloszlású a intervallumon.
Mutassuk meg, hogy a Bertrand probléma megoldása
A Bertrand kísérletben válasszuk az egyenletes szögmodellt. Végezzük el a kísérletet 1000-szer, 10-esével frissítve. Figyeljük meg a húr esemény relatív gyakoriság függvényének a valószínűséghez való nyilvánvaló konvergenciáját.
Használja fel a változók felcserélésének a formuláját, hogy változó sűrűségfüggvénye a következő
Használja fel a változók felcserélésének a formuláját, hogy -nek van sűrűségfüggvénye
Megjegyezzük, hogy és nem egyenletes eloszlású.
Mutassuk meg, hogyan szimuláljuk a , , , és változókat felhasználva a véletlen számokat.
Tételezzük fel, hogy egyenletes eloszlású a intervallumon.
Mutassuk meg, hogy a Bertrand probléma megoldása
A Bertrand kísérletben válasszuk az egyenletes végpont modellt. Végezzük el a kísérletet 1000-szer, 10-esével frissítve. Figyeljük meg a húr esemény relatív gyakoriság függvényének a valószínűséghez való nyilvánvaló konvergenciáját.
Használja fel a változók felcserélésének a formuláját, hogy -nek van sűrűségfüggvénye
Használja fel a változók felcserélésének a formuláját, hogy -nak van sűrűségfüggvénye
Megjegyezzük, hogy és nem egyenletes eloszlású; valójában béta eloszlású, és a két paraméter 2 és 1.
Tételezzük fel, hogy egy véletlen húrt generálunk egy egységsugarú pénzérme feldobásával, melyet egy párhuzamos vonalakból álló táblán végzünk, a vonalak távolsága 2 egység. Melyik model írja le ezt a fizikai kísérletet (ha van ilyen modell)?
Tételezzük fel, hogy egy tű hozzá van erősítve egy egységsugarú korong széléhez. Egy véletlen húrt generálhatunk a tű forgatásával. Melyik modell írja le ezt a fizikai kísérletet (ha van ilyen modell)?