A Buffon féle kísérletek nagyon régi és híres véletlen kísérletek, nevüket Buffon grófról kapták. Ezek a kísérletek voltak a geomatriai valószínűség első problémái.
A Buffon féle érmekísérletben egy érmét azonos négyzet alakú csempékkel fedett padlóra dobunk. Az az esemény érdekel minket, hogy az érme ráesik-e a csempéket elválasztó vonalra. Az, hogy a csempék oldalhosszát 1-nek vesszük, ekvivalens azzal, mintha a csempék oldalhosszát tekintenénk mérési egységnek.
Először is definiáljuk a kísérletet matematikai szempontból. Szokás szerint a fizikai objektumot idealizáljuk, feltételezve, hogy az érme szabályos kör alakú, sugárral, és a padlólapokat elválasztó hézagok egyenes szakaszok. Természetesen ahhoz, hogy megadjuk a kísérlet eredményét (kimenetelét), fel kell jegyeznünk az érme középpontjának helyzetét azon csempe középpontjához viszonyítva, ahova az érme esik. Pontosabban meg kell adnunk egy koordinátarendszert, melynek középpontja annak a csempének a közepe, amelyiken az érme középpontja is elhelyezkedik
Amikor az érmét feldobtuk, jelöljük leesése utáni koordinátáit -nal, ahol a minta terünk, és az alap valószínűségi változónk. Végül tételezzük fel, hogy azért, hogy legalább az lehetséges legyen, hogy az érme négyzet belsejébe essen anélkül, hogy átmenne választóvonalon.
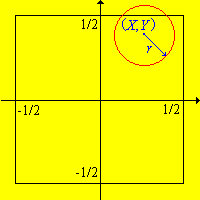
A következőkben definiálnunk kell egy megfelelő valószínűségi mezőt, hogy le tudjuk írni az
alap véletlen vektort.
Ha az érme véletlenszerűen
esik a padlóra, akkor természetesen feltételezhetjük, hogy
egyenletes eloszlású az
mintatéren. Definíció szerint ez azt jelenti, hogy
Futtassuk le a Buffon féle érmekísérletet a alapértelmezett beállításokkal! Figyeljük meg, hogy a pontok mennyire egyenletes módon töltik ki az mintateret!
Minket az a esemény érdekel, amikor az érme keresztezi az elválasztó vonalat. Azonban könnyebb előállítani a komplementer eseményt, ami a nem keresztezést jelenti.
Mutassuk meg, hogy
Felhasználva a 2. gyakorlat eredményét mutassuk meg, hogy A grafikonja, mint , függvénye az alábbi:
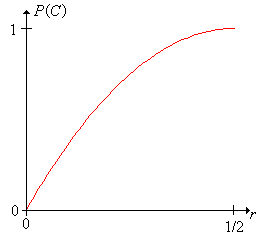
A Buffon féle érmekísérletben változtassuk a sugarat a görgetősávval és figyeljük meg, hogyan változnak a és a események. Végezzük el a kísérletet különböző értékeivel és hasonlítsuk össze a fizikai kísérletet a szóródási diagramon lévő pontokkal! Figyelje meg, hogy láthatóan a relatív gyakorisága a a valószínűségéhez konvergál!
Egy esemény relatív gyakoriságának konvergenciája ( ahogy a kísérletet ismételgetjük ) az esemény valószínűségéhez a nagy számok törvényének egy speciális esete.
Végezzük el a Buffon féle érmekísérletet egy egységnyi oldalhosszúságú szabályos háromszögeket tartalmazó síkon!
Mutassuk meg, hogyan szimuláljuk az érme középpontját a Buffon féle érmekísérletben, felhasználva a véletlen számokat!
A Buffon féle tűkísérlet abból áll, hogy egy tűt dobunk egy fapadlóra. A minket érdeklő fő esemény az, hogy a tű keresztezi-e a fapadló léceinek "határvonalait". Különösképpen érdekes, hogy ennek az eseménynek a valószínűsége a statisztikai becsléséhez vezet!
Először definiáljuk a kísérletet matamatikailag. Újra idealizáljuk a fizikai objektumot feltételezve, hogy a fapadló egyforma lécekből áll, a lécek egységnyi szélességűek. A tű hossza legyen , ilymódon a tű nem keresztez egynél több léchatárvonalat. Végül feltesszük, hogy a fapadló lécei közötti hézagok és a tű egyenes szakaszok.
Amikor a tűt feldobtuk, feljegyezzük annak relatív irányát a fapadló réseihez képest. Ugyanakkor feljegyezzük azt az szöget, amit a tű felső fele bezár a tű közepén átmenő, a fapadló léceivel párhuzamos egyenessel és azt az értéket, amely megadja a tű közepének a megfelelő fapadló léc alsó vonalától való távolságát. Ezek lesznek kísérletünk alap véletlen változói, és így a a kísérlet mintatere
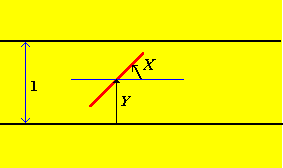
Újból tételezzük fel, hogy modellünkben a tűt véletlenszerűen
ledobjuk a padlóra. Így elfogadható matematikai feltevés lehet az, hogy az alap véletlen vektor
(,
) egyenletes eloszlású a mintatér felett. Definíció szerint ez azt jelenti, hogy
Futtassuk le a Buffon féle tűkísérletet a alapértelmezett beállításokkal és figyeljük meg, hogy a pontok mennyire egyenletes módon töltik ki az mintateret!
Minket a eseménnyel kapcsolatban a érdekel, hogy a tű keresztezi-e a lécek határvonalát.
Trigonometriai ismereteket használva mutassuk meg, hogy esemény a szög és a távolságváltozók segítségével az alábbi módon adható meg:
Az és az a szóródási diagramon kék színnel mutatják a Buffon féle tűkísérletet, és hogy a esemény az alsó görbe alatti és a felső görbe feletti tartományok egyesítése. Így, a tű pontosan akkor metsz léchatárvonalba, ha a pont ebbe a tartományba esik.
Mutassuk meg, hogy és ezért . A grafikonja, mint -nek a függvénye, a következő:
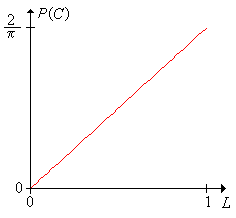
A Buffon féle tűkísérletben változtassuk a tű hosszát a görgetősávval és figyeljük meg, hogyan változnak a és a események. Végezzük el a kísérletet különböző értékeivel és hasonlítsuk össze a fizikai kísérletet a szóródási diagram pontjaival. Figyelje meg, hogy láthatóan a relatív gyakorisága a valószínűségéhez konvergál.
Egy esemény reatív gyakoriságának ( ahogy a kísérletet ismételgetjük ) az esemény valószínűségéhez való konvergenciája a nagy számok törvényének speciális esete.
Adjuk meg a Buffon féle tűkísérletben a következő események valószínűségét. Mindegyik esetben vázoljuk az eseményt, mint a mintatér egy részhalmazát.
Tételezzük fel, hogy a Buffon féle tűkísérletet nagyon sokszor végezzük el. A nagy számok törvénye miatt a léc határvonalának átmetszésének az aránya ugyanaz, mint a léc határvonalának átmetszésének a valószínűsége. Pontosabban jelöljük az első kísérlet során az átmetszések számát -nel. Megjegyezzük, hogy egy összetett eseményre vonatkozó valószínűségi változó, amely az alap tűkísérlet -szer történő megismétléséből áll. Így, ha nagy, akkor
Ez Buffon -re vonatkozó híres becslése. A Buffon féle tűkísérlet szimulációjában ezt a becslést mindegyik futtatásra kiszámítja az applet a második táblázatban megjelenik numerikusan, az oszlopdiagramban vizuálisan.
Végezzük el a Buffon féle tűkísérletet az alábbi tűhosszakkal . Mindegyik esetben figyeljük meg becslélést a szimuláció futása alatt.
Gondosabban elemezzük a becslési problémát. A -edik futásnál vezessük be az alábbi indikátor vátozót
Ezek az indikátorváltozók függetlenek, azonos eloszlásúak, mivel feltehetően a megismételt kísérletek függetlenek. Így, a sorozat egy u.n. Bernoulli kísérlet folyamatot alkot.
Mutassuk meg, hogy az első futtatás során a metszések száma
Felhasnálva a 14. gyakorlat eredményét mutassuk meg, hogy az első futtatás során a metszések száma binomiális eloszlású és paraméterekkel.
Felhasználva a 15. gyakorlat eredményét, mutassuk meg, hogy az átmetszések számának várható értéke és szórásnégyzete
Felhasználva a nagy számok erős törvényét mutassuk meg, hogy 1 valószínűséggel
Így van két nyilvánvaló elemi becslésünk:
becslésének van néhány fontos statisztikai tulajdonsága. Elöször is ez torzítatlan becslés, mert várható értéke megeyezik a becsült paraméterrel:
Felhasználva a 16. gyakorlat és a várható érték tulajdonságait mutassuk meg, hogy
Mivel a becslés torzítatlan, a szórásnégyzet az átlagos négyzetes hibát adja:
Felhasználva a 16. gyakorlat és a szórásnégyet tulajdonságait mutassuk meg, hogy
Mutassuk meg, hogy a szórásnégyzet a tű hosszának növekvő függvénye.
Így becslése javítható, amint a tű hosszát növeljük. Másrészt becslése torzított; -t túbecsli:
Felhasználva a Jensen egyenlőtlenséget mutassuk meg, hogy
becslése szintén javul, ahogy a tű hossza növekszik. Ezt matematikailag nem könnyű belátni. De empirikusan belátható.
A Buffon féle tűkisérletben a gyakoriságot változtassuk 100-ig. Végezzük el a kísérletet 5000-szer az alábbi hosszak mindegyikére: , , , és . Figyeljük meg, hogy mennyire működik jól a becslés az egyes esetekben!
Végül meg kell jegyeznünk, hogy gyakorlati szempontból a Buffon féle tűkísérlet nem túl hatékony módszer a becslésére. Richard Durrett munkája szerint becslése négy tizedejegy pontossággal, hosszúságú tűvel, nagyjából 100 millió feldobást igényelt!
Végezzük el a Buffon féle tűkísérletet úgy, hogy 100-asával frissítünk , amíg π értékét két tizedesjegy pontossággal megközelítjük. Jegyezzük fel a kísérletek számát. Próbáljuk meg ezt a kísérletet elvégezni az alábbi tűhosszakkal is , , , és majd hasonlítsuk össze az eredményeket.
Mutassuk meg, hogyan tudjuk szimulálni az szöget és az távolságot a Buffon féle tűkísérletben a véletlen számok használatával.
A Buffon féle tűprobléma lényegében a Monte-Carlo integrálással megoldható. Általában, a Monte-Carlo módszerek használhatók problémák közelítő megoldásához statisztikai minták segítségével, amikor a probéma analitikusan nehezen oldható meg. A Monte-Carlo módszerek modern elmélete Stanislaw Ulamnak köszönhető, aki a hidrogénbomba fejlesztésével kapcsolatban használta a módszereket.
Az eredeti tűprobléma sokféleképpen terjeszthető ki, kezdve Simon Laplaceszal, aki derékszögű csempés padlóval vizsgálta a problémát. Valóban, a probléma variációi napjainkban is aktív kutatási problémákat adnak.
Neil Weiss rámutatott arra, hogy a Buffon féle tűprobléma számítógépes szimulációja egy önmagára hivatkozó probléma abban az értelemben, hogy feltételezzük ismeretét. (ezt a 24. gyakorlatból láthatja.)
Próbáljon megadni olyan számítógépes algoritmust a Buffon féle tűproblémára, ami nem feltételezi értékének, vagy más transcendens számnak az ismeretét!