Tételezzük fel, hogy egy pálcát véletlenszerűen két helyen eltörünk. Mi a valószínűsége, hogy a három pálcadarabból háromszög alkotható?
Vizsgálódás nélkül végezzünk egy becslést.
Végezzük el a háromszög kísérletet 50-szer. Nem törődve az applet által kijelzett információk mindegyikével, de pontosan jegyezzük fel, vajon a darabokból tudunk-e háromszöget alkotni. Vajon módosítani akarjuk az 1. gyakorlatban adott becslésünket?
Ahogy szokás, első lépésként matematikailag modellezzük a véletlen kísérletet. Tekintsük a pálca hosszát a mérési egységnek, így pálcát a intervallummal tudjuk azonosítani. A pálca három darabra töréséhez az intervallumban meg kell adnunk két pontot. Így jelölje az első pontot és a második pontot. Megjegyezzük, hogy és véletlen változók és így kísérletünk mintatere:
Most, hogy modellezzük az állítást, hogy a pontokat véletlenszerűen választjuk, tételezzük fel, mint az előző részben, hogy és független , s mindegyikük egyenletes eloszlású a intervallumon.
Mutassuk meg, hogy egyenletes eloszlású a -en.
Innen következik, hogy
Bizonyítsuk be, hogy a három pálcadarabból akkor és csak akkor rakható ki háromszög, ha teljesülnek a háromszög egyenlőtlenségek: két darab hosszának összege nagyobb, mint a harmadik darab.
Mutassuk meg, hogy az az esemény, hogy a három pálcadarabból háromszög rakható össze, a következő: ahol
Váoljuk a eseményt. Érdekes módon, a háromszögekből tevődik össze!
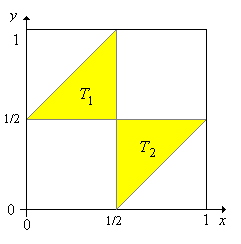
Mutassuk meg, hogy .
Mennyire sikerült ehhez közeli értékre tippelnie az 1. gyakorlatban? A 6. gyakorlatban a valószínűség relatíve alacsony értéke meglepő.
Végezzük el a háromszög kísérletet 1000-szer, 10-esével frissítgetve. Figyeljük meg, hogy empirikus valószínűsége jól láthatóan a valódi valószínűséghez konvergál.
Most ki fogjuk számolni annak valószínűségét, hogy a pálcikadarabok adott típusú háromszöget alkotnak. Emékeztetünk arra, hogy egy hegyesszögű háromszögben mind a három szög kisebb, mint 90°, míg egy tompaszögű háromszögnek pontosan egy olyan szöge van, amely nagyobb, mint 90°. Egy derékszögű háromszögben természetesen egy 90°-os szög van.
Tételezzük fel, hogy a háromszög oldalának hosszai rendre , , és , ahol a legnagyobb oldal. Emlékeztetünk arra (vagy mutassuk meg), hogy egy háromszög
A (c) rész a jól ismert Pitagorasz tétel, amely az ókori görög matematikusról, Pitagoraszról kapta a nevét.
Mutassuk meg, hogy a derékszögű háromszög esetén a pálcikadarabok hosszára felírt egyenlőségek a következők:
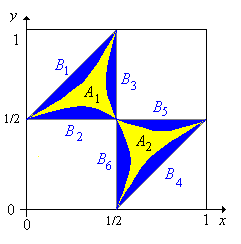
Jelölje azt az eseményt, hogy a pálcikadarabok derékszögű háromszöget alkotnak, Mutassuk meg, hogy
Mutassuk meg: az az esemény, hogy a pálcikadarabokból hegyesszögű háromszög alkotható ahol
Mutassuk meg: az az esemény, hogy a pálcikadarabokból tompaszögű háromszög alkotható ahol
Mutassuk meg, hogy
Bizonyítsuk be a szimmetria felhasználásával, hogy
A szimmetria felhasználásával még be tudjuk bizonyítani, hogy minden -re ugyanaz, annak ellenére, hogy (pédául) és nem egybevágóak.
Mutassuk meg, hogy
Futtassuk le a háromszög kísérletet 1000-szer,10-esével frissítve. Figyeljük meg, hogy az empirikus valószínűség konvergenciája a valódi valószínűséghez nyilvánvaló.