

Kiindulási pontunk, mint általában, most is egy véletlen kísérlet a hozzá tartozó valószínűségi mezővel, és az azon értelmezett valószínűségi mértékkel. Ebben a fejezetben két olyan függvénnyel foglalkozunk, amelyekkel gyakran szokták jellemezni az eloszlásokat.
Legyen egy valós értékű valószínűségi változó. Ekkor eloszlásfüggvénye az az függvény, amelyre
Mint láthatjuk, az eloszlásfüggvény definíciója nem függ attól, hogy a változó eloszlása diszkrét, folytonos, vagy keverék, és az is igaz, hogy ha ismerjük az eloszlásfüggvényt, akkor eloszlása egyértelműen meghatározott. A következő ábrán a világoskék rész egy folytonosan elkent eloszlást ábrázol, a sötét pontok pedig olyanok, melyeket pozitív valószínűséggel vesz fel a valószínűségi változónk. Ekkor az pontban és a tőle balra lévő összes súlyt adja meg (itt jegyezzük meg, hogy a szakirodalom az eloszlásfüggvény definícióját tekintve nem teljesen egységes, egyes szerzők az pont súlyát már nem veszik figyelembe, azaz náluk

Az függvény néhány határértékére gyakran fogunk hivatkozni, ezért bevezetjük az alábbi jelöléseket:
A következő feladatokban az eloszlásfüggvények alaptulajdonságait bizonyítjuk. Ezeknek az állításoknak a megfordítása is igaz a következő értelemben: egy függvény eloszlásfüggvény, ha az alábbi tulajdonságokkal rendelkezik.
Igazoljuk, hogy növekvő, azaz ha akkor .
Igazoljuk, hogy minden esetén, azaz jobbról folytonos.
Igazoljuk, hogy minden esetén, azaz -nek mindenütt létezik a baloldali határértéke.
Igazoljuk, hogy .
Igazoljuk, hogy .

A következő feladatban azt látjuk be, hogy az eloszlásfüggvény segítségével meghatározható annak a valószínűsége, hogy egy tetszőleges intervallumba esik. Mint már korábban említettük, tetszőleges -en értelmezett valószínűségi eloszlást egyértelműen meghatároznak az intervallumok valószínűségei, így a következő feladat következménye, hogy az eloszlásfüggvény is egyértelműen meghatározza eloszlását. Mindegyik részfeladat megoldásához fontos segédeszköz a következő összefüggés:
Tegyük fel, hogy . Igazoljuk, hogy
Az előző feladatok megfordítása a következőképp igaz: ha egy -en értelmezett függvényre igazak az 1.-5. feladatokban leírt tulajdonságok, akkor a 6. feladatban adott formulák egy valószínűségeloszlást határoznak meg -en, melynek az eloszlásfüggvénye.
Igazoljuk, hogy pontosan akkor folytonos eloszlású, ha az eloszlásfüggvénye, , folytonos.
Egy valószínűségi változó eloszlás-, illetve súly- és sűrűségfüggvénye szoros kapcsolatban állnak egymással, ezt elemezzük a következő feladatokban
Tegyük fel, hogy diszkrét eloszlású az diszkrét halmazon, és jelölje a súlyfüggvényét, pedig az eloszlásfüggvényét. Igazoljuk, hogy minden esetén
Megfordítva, igazoljuk, hogy -re
Tehát azt kaptuk, hogy diszkrét esetben egy lépcsős függvény; szakadási pontjainak halmaza ; és az pontban lévő ugrásának nagysága épp a súlyfüggvényének értéke -ben.

Sűrűségfüggvénnyel rendelkező folytonos eloszlású (vagy más szóval abszolút folytonos eloszlású) valószínűségi változókra hasonló állítás igaz:
Tegyük fel, hogy folytonos eloszlású -en sűrűségfüggvénnyel (amiről feltesszük, hogy szakaszonként folytonos), és eloszlásfüggvénnyel. Igazoljuk, hogy minden esetén
Megfordítva, igazoljuk, hogy ha folytonos -ben, akkor deriválható -ben, és

Az előző feladatban megfogalmazott állítás egy analízisbeli alapvető fontosságú tétel speciális esete. Keverék eloszlásokra az előző két feladat állításainak keveréke
igaz:
Tegyük fel, hogy keverék eloszlású, diszkrét része az megszámlálható halmazon értelmezett, folytonos része pedig a valós számokon. Jelölje a diszkrét részhez tartozó (parciális) súlyfüggvényt, a folytonos részhez tartozó (parciális) sűrűségfüggvényt, pedig az eloszlásfüggvényt. Igazoljuk, hogy
Természetesen feltételes eloszlások esetén is definiálható az eloszlásfüggvény, és a fenti eredmények ilyenkor is érvényesek.
Tegyük fel, hogy folytonos eloszlású -en, és sűrűségfüggvénye szimmetrikus -ra, azaz:
Igazoljuk, hogy ekkor az eloszlásfüggvényre
Legyen az valószínűségi változó eloszlásfüggvénye . Az alábbi, úgynevezett túlélési függvény nyilván ugyanannyi információt hordoz, mint :
Az 1. Feladatban megfogalmazott tulajdonságok megfelelőit mondjuk ki, és lássuk be a túlélési függvényekre!
Tegyük fel, hogy egy -en folytonos eloszlású valószínűségi változó. Ha egy alkatrész élettartama, akkor a túlélési függvényt nevezhetjük megbízhatósági függvénynek, hiszen pont annak a valószínűsége, hogy az alkatrész időegység elteltével is üzemel. A következő függvényt pedig nevezhetjük a hiba rátafüggvényének:
Igazoljuk, hogy ha kicsi.
Tehát annak a valószínűsége, hogy a alkatrész a következő időegység alatt tönkremegy, feltéve, hogy ideig üzemelt. Továbbá a hiba rátafüggvénye egyértelműen meghatározza eloszlását:
Igazoljuk, hogy
Igazoljuk, hogy a hiba rátafüggvényre:
Az előző feladat megfordításaként tegyük fel, hogy teljesíti a 15. feladat tulajdonságait. Igazoljuk, hogy a 14. feladatbeli formulával definiált függvény egy megbízhatósági függvény!
Legyenek és egy közös véletlen kísérlettől függő valós értékű valószínűségi változók, azaz egy -beli véletlen vektor. Ekkor az pár eloszlásfüggvénye a következő függvény:
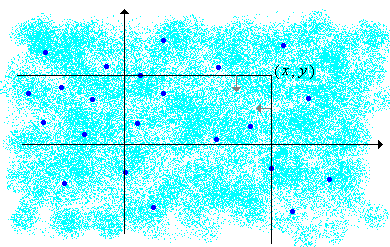
A fenti ábrán a világoskék rész egy folytonosan elkent eloszlást ábrázol, a sötét pontok pedig olyanok, melyeket pozitív valószínűséggel vesz fel a véletlen vektorunk. Tehát az a súly, melyet a valószínűség eloszlás az ponttól balra és lefelé lévő síknegyedhez rendel. Ugyanúgy, mint az egyváltozós esetben, eloszlásfüggvénye most is egyértelműen meghatározza az pár eloszlását.
Legyenek , , , valós számok, melyekre és . Igazoljuk, hogy
Az előző feladat segítségével általánosítsuk a 6. feladat eredményét, azaz a kisebb és a nem nagyobb relációk minden lehetséges kombinációjára fejezzük ki a megfelelő valószínűségeket az eloszlásfüggvénnyel!
Legyen az pár eloszlásfüggvénye, és pedig és eloszlásfüggvényei. Igazoljuk, hogy
Az előző feladat jelöléseivel igazoljuk, hogy és pontosan akkor függetlenek, ha
A fenti definíció és valamennyi állítás természetes módon általánosítható dimenziós véletlen vektorokra.
Tegyük fel, hogy adott egy minta valamilyen valós értékű valószínűségi változó realizációiból. Ekkor definiálhatjuk az eloszlás ezen minta alapján kapott empirikus (vagy tapasztalati) eloszlásfüggvényét a következő módon:
Tehát az -nél kisebb, vagy egyenlő mintaelemek relatív gyakorisága.
Legyen egy valószínűségi változó eloszlásfüggvénnyel, és legyen . Ekkor azt az értéket, amelyre
az eloszlás -kvantilisének nevezzük. Durván szólva a -kvantilis az az érték, ahol az eloszlásfüggvény áthalad (vagy átugrik) a értéken. Például a következő ábrán az egyetlen -kvantilis, és az egyetlen -kvantilis. Viszont -kvantilis az egész intervallum, míg minden -beli számhoz rendelt kvantilis értéke.

Vegyük észre, hogy a kvantilis- és az eloszlásfüggvény lényegében egymás inverzei, azonban ez nem pontosan a hagyományos inverz függvény reláció, hisz az eloszlásfüggvény általában nem kölcsönösen egyértelmű. Néha hasznos, ha garantálni tudjuk, hogy minden -hez egyértelműen választható kvantilis, ezért definiáljuk az eloszlásfüggvény általánosított inverzét:
Legyen . Annak segítségével, hogy jobbról folytonos és növekvő, igazoljuk, hogy egy alakú intervallum!
Így definiálhatjuk a kvantilisfüggvényt a következő módon:
Vegyük észre, hogy a 21. feladat értelmében a definíció értelmes. Továbbá ha szigorúan monoton módon nő fel nulláról egyre az intervallumon (vagyis az eloszlás folytonos, és -re koncentrált), akkor az függvény hagyományos értelemben vett inverze. Általában nem szokás a kvantilis függvényt definiálni a nulla és az egy pontokban. Ha mégis definiálnánk, akkor mindig lenne.
A következő feladatban azt látjuk be, hogy az elnevezés helyes, valóban egy -kvantilis.
Tetszőleges -re igazoljuk, hogy
A többi alaptulajdonságot a következő két feladat tartalmazza.
Igazoljuk, hogy
Mint mindig, az inverz képzés most is lényegében azt jelenti, hogy megcseréljük a független és a függő változó szerepét. Az alábbi rajzon is látható, hogy szakadási pontjainak esetén konstans szakaszok felelnek meg, és fordítva, -en egy folytonos szakasz egy szakadást eredményez -ben.
 |
 |
Igazoljuk, hogy tetszőleges és esetén akkor és csak akkor, ha .
Az
-kvantilist nevezik az eloszlás mediánjának. Ha a medián egyértelmű, akkor azt tekinthetjük az eloszlás középpontjának. Az
-kvantilist szokás alsó kvantilisnek, a
-kvantilist pedig felső kvantilisnek nevezni. Ezzel a terminológiával élve a medián a középső kvantilis. Feltéve, hogy ezek a kvantilisek egyértelműek, jelölje
,
és
az
eloszlás alsó, középső és felső kvantilisét. Ekkor az
-től
-ig terjedő intervallum az eloszlás középső fele
, ennek a hosszát nevezik interkvantilis terjedelemnek:
(a jelölés az angol interquartile range kifejezés rövidítése). Az interkvantilis terjedelem bizonyos értelemben az eloszlás medián körüli szóródását méri. Legyen illetve az eloszlás minimális és maximális értékei (feltesszük, hogy ezek végesek). Ekkor az
paraméterek elég sok információt hordoznak az eloszlás középpontjáról, elkentségéről, ferdeségéről. Ezért gyakran ábrázolják ezt az öt paramétert grafikusan egy úgynevezett boxplot (vagy doboz diagram) ábrán, amelyen egy vonalat húznak az minimális értéktől a maximális értékig, egy téglalap alakú dobozt -től -ig, és vízszintes vonallal jelölik az , és értékeit. Ekkor az öt paraméter lehetséges értékeit négy olyan részre osztja, melyek mindegyikének a valószínűsége.

Tegyük fel, hogy folytonos eloszlású valós értékű valószínűségi változó sűrűségfüggvénnyel, amely szimmetrikus az pontra, azaz . Igazoljuk, hogy az eloszlás -kvantilise, akkor az eloszlás -kvantilise.
Legyen a következő függvény:
Legyen a következő függvény:
Legyen a következő függvény:
Tegyük fel, hogy sűrűségfüggvénye , azaz egyenletes eloszlású az intervallumon.
Tegyük fel, hogy sűrűségfüggvénye , ahol paraméter.
Az előző feladatban szereplő eloszlást nevezik paraméterű exponenciális eloszlásnak. Ezt az eloszlást karakterizálja az a tulajdonsága, hogy a hiba rátája konstans. Az exponenciális eloszlással részletesen a Poisson folyamatról szóló fejezetben foglalkozunk.
A kvantilis appletben válasszuk a gamma eloszlást, és állítsuk be a paraméterértéket, így visszakapjuk az exponenciális eloszlást. Változtassuk a skálaparaméter értékét (ami a ráta reciproka), és figyeljük meg, hogyan változik a sűrűségfüggvény és az eloszlásfüggvény alakja!
Tegyük fel, hogy sűrűségfüggvénye , amint , ahol paraméter.
Az előző feladatban szereplő eloszlást Vilfredo Pareto tiszteletére paraméterű Pareto eloszlásnak nevezik. A Pareto eloszlással részletesen a Nevezetes eloszlások című fejezetben foglalkozunk.
A kvantilis appletben válasszuk ki a Pareto eloszlás! Változtassuk a paraméter értékét, és figyeljük meg, hogyan változik a sűrűségfüggvény és az eloszlásfüggvény alakja!
Tegyük fel, hogy sűrűségfüggvénye .
Az előző feladatban szereplő eloszlást Augustin Cauchy tiszteletére Cauchy eloszlásnak nevezik. A Cauchy eloszlás a Student féle eloszláscsalád tagja. A Student féle eloszlásokról részletesen a Nevezetes eloszlások fejezetben olvashatunk.
A kvantilis appletben válasszuk a Student eloszlásokat, majd a szabadsági fokok számát válasszuk egynek, így megkapjuk a Cauchy eloszlást. Figyeljük meg a sűrűség- és az eloszlásfüggvény alakját!
Legyen , ahol paraméter
Az előző feladatban szereplő eloszlást Walodi Weibull tiszteletére paraméterű Weibull eloszlásnak nevezik. A Weibull eloszlással részletesen a Nevezetes eloszlások című fejezetben foglalkozunk.
A kvantilis appletben válasszuk a Weibull eloszlást! Változtassuk a paraméter értékeit, és figyeljük meg a sűrűség- és az eloszlásfüggvény alakját!
Tegyük fel, hogy sűrűségfüggvénye .
Tegyük fel, hogy sűrűségfüggvénye .
Az előző két feladatban tekintett eloszlások béta eloszlások. Az utolsó feladatban tekintett eloszlást - az eloszlásfüggvénye miatt - arkusz szinusz eloszlásnak is nevezik. A Béta eloszlásokkal részletesen a Nevezetes eloszlások című fejezetben foglalkozunk.
A kvantilis appletben válasszuk a béta eloszlást! A következő paraméterértékek mindegyikére figyeljük meg a a sűrűség- és az eloszlásfüggvény helyzetét és alakját!
Legyen .
Az előző feladatban tekintett eloszlás a logisztikus eloszlás, melynek kvantilisfüggvényét logisztikus függvénynek nevezik. A logisztikus eloszlást részletesen a Nevezetes eloszlásokról szóló fejezetben tárgyaljuk.
A kvantilis appletben válasszuk a logisztikus eloszlást, és figyeljük meg a a sűrűség- és az eloszlásfüggvény alakját!
Legyen .
Az előző feladatban szereplő eloszlást nevezik első típusú extrémérték eloszlásnak, vagy más néven Gumbel eloszlásnak (Emil Gumbel tiszteletére). Az Extrémérték eloszlásokkal részletesen a Nevezetes eloszlások című fejezetben foglalkozunk.
A kvantilis appletben válasszuk az extrémérték eloszlást, és figyeljük meg a a sűrűség- és az eloszlásfüggvény helyzetét és alakját!
Tegyük fel, hogy sűrűségfüggvénye .
A hisztogram appletben válasszuk a doboz diagramot, és állítsuk be a szélesség értékét 0,1-re. Az alábbi esetek mindegyikéhez konstruáljunk egy diszkrét eloszlást, és annak legalább 30 realizációját. Vizsgáljuk meg a doboz diagram alakját és az öt paraméter egymáshoz viszonyított relatív helyzetét!
Feldobtunk két dobókockát, és a dobott számokat az vektorba lejegyeztük.
Az pár együttes sűrűségfüggvénye .
Az M&M adathalmazban határozzuk meg az egy zacskóban lévő cukorkák empirikus eloszlásfüggvényét!
A kabóca adathalmazban jelölje a testhosszt, pedig a nemet. Határozzuk meg az alábbi valószínűségi változók empirikus eloszlásfüggvényét:
Az ebben a fejezetben tárgyalt fogalmak jelentős részének fontos statisztikai megfelelője definiálható. Ezekről részletesen a Véletlen minták fejezetben olvashatunk, azon belül is leginkább az empirikus eloszlásokról és a rendezett statisztikákról szóló részekben.