]> Folytonos eloszlások
  1. Virtual Laboratories
  2. 2. Eloszlások
  3. 1
  4. 2
  5. 3
  6. 4
  7. 5
  8. 6
  9. 7
  10. 8

2. Folytonos eloszlások

Általános elmélet

Kiindulási pontunk, mint általában, most is egy véletlen kísérlet a hozzá tartozó Ω valószínűségi mezővel és az azon értelmezett valószínűségi mértékkel. Egy S n -értékű X valószínűségi változóról azt mondjuk, hogy folytonos eloszlású, ha

X x 0  minden   x S  esetén.  

Első ránézésre ellentmondásnak tűnhet, hogy X tetszőleges értéket nulla valószínűséggel vesz fel. Azonban ez mégsem ellentmondás, mert nagyon sok lehetséges x érték van. Ugyanez a jelenség az is, hogy egy -beli intervallum lehet pozitív hosszúságú annak ellenére, hogy nulla hosszúságú pontokból áll, vagy hogy 2 egy részhalmaza lehet pozitív területű annak ellenére, hogy nulla területű pontokból (vagy görbékből) áll.

Igazoljuk, hogy X C 0 tetszőleges megszámlálható C S esetén!

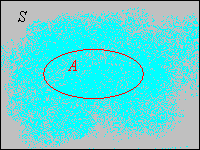
Tehát a folytonos eloszlások alapvetően eltérnek a diszkrétektől, ahol a teljes eloszlás egy megszámlálható halmazra koncentrálódik. Ezzel ellentétben a folytonos esetben a tömegeloszlás egész S -en folytonosan van elkenve. Vegyük észre továbbá, hogy maga S nem lehet megszámlálható. Az alábbi képen a világoskék felhő szimbolizál egy folytonos eloszlást a síkon.

A continuous distribution

Sűrűségfüggvények

Tegyük fel, hogy X folytonos eloszlású S n -en. Egy S -en értelmezett, valós értékű f függvényt az X valószínűségi változó sűrűségfüggvényének (vagy valószínűségi sűrűségfüggvényének) nevezünk, ha f -re igazak az alábbiak:

  1. f x 0 ,  x S ,
  2. x S f x 1 ,
  3. x A f x X A ,  A S .
A continuous distribution

A fenti definíció (c) pontja azért is nagyon fontos, mert ennek következménye, hogy X eloszlását egyértelműen meghatározza a sűrűségfüggvénye. Fordítva, minden függvény, amely teljesíti az (a) és (b) pontokat, egy valószínűségi sűrűségfüggvény, és egy ilyen függvényből a (c) pont segítségével előállíthatunk egy folytonos eloszlást S -en.

Ha n 1 , akkor a (b) és (c) pontokban lévő integrálok többváltozósak, és n valamely részhalmaza felett értelmezettek, továbbá x x 1 x 2 x n és x x 1 x 2 x n . Matematikailag precíz módon fogalmazva f a szokásos n -dimenziós (Lebesgue) mértékre vonatkozó sűrűségfüggvény, amely mérték a

n A x A 1 ,  A n

képlettel definiálható. Vegyük észre, hogy n S pozitív kell, hogy legyen (esetleg lehet végtelen is). Speciálisan,

  1. ha n 1 , S egy -beli pozitív hosszúságú részhalmaz;
  2. ha n 2 , S egy 2 -beli, pozitív területű részhalmaz;
  3. ha n 3 , S egy 3 -beli pozitív térfogatú részhalmaz.

A fenti alacsony dimenziós esetek ( n 1 2 3 ) szemléltetés szempontjából hasznosak, de más, kitüntetett szerepük nincs. Az érdekes véletlen kísérletekben általában több valószínűségi változó (azaz egy véletlen vektor) is megjelenik. Vegyük észre továbbá, hogy egy f sűrűségfüggvény mindig kiterjeszthető az egész n -re úgy, hogy f x 0 ,  x S . Ez a kiterjesztés néha leegyszerűsítheti a jelöléseket.

Az olyan x S elemet, amelyre az f sűrűségfüggvény maximális, az eloszlás móduszának nevezzük.

A folytonos eloszlások sűrűségfüggvénye lényegesen különbözik a diszkrét súlyfüggvényektől a következők miatt:

Sűrűségfüggvények konstrukciója

Tegyük fel, hogy g egy nemnegatív függvény S n -en. Legyen

c x S g x .

Igazoljuk, hogy ha 0 c , akkor f x 1 c g x ,  x S egy valószínűségi sűrűségfüggvényt definiál S -en!

Vegyük észre, hogy f g -nek egy skálázottja. Így az előző feladat értelmében előállíthatunk előírt tulajdonságú sűrűségfüggvényt (megfelelő tartományon értelmezettet, bizonyos alakút, vagy szimmetria tulajdonságokkal rendelkezőt, stb.). A c konstanst normáló konstansnak nevezzük.

Feltételes sűrűségek

Tegyük fel, hogy X egy S n értékű folytonos valószínűségi változó f sűrűségfüggvénnyel. Ekkor f nyilván függ az Ω eseménytéren értelmezett valószínűségi mértéktől. Ez a mérték lehet feltételes valószínűségi mérték valamely E Ω feltétellel (ekkor persze E 0 ). A szokásos jelölés:

f x E ,  x S .

Vegyük észre, hogy a jelöléstől eltekintve semmilyen új fogalmat nem definiáltunk. Azaz az előző függvény egy folytonos eloszlás valószínűségi sűrűségfüggvénye, azaz teljesíti az (a) és (b) pontokat, míg a (c) pont jelen esetben

x A f x E X A E ,  A S .

Minden, a sűrűségfüggvényekre vonatkozó általános állítás megfelelője igaz feltételes sűrűségfüggvényekre is.

Legyen B S úgy, hogy X B x B f x 0 . Igazoljuk, hogy X feltételes sűrűsége az X B feltétel mellett

f x X B f x X B x B 0 x B .

Példák, alkalmazások

Az exponenciális eloszlás

Legyen f t r r t ,  t 0 , ahol r 0 paraméter.

  1. Igazoljuk, hogy f egy valószínűségi sűrűségfüggvény!
  2. Vázoljuk f -et, és határozzuk meg a móduszát!

Az előző feladatban szereplő sűrűségfüggvény az r paraméterű exponenciális eloszlás sűrűségfüggvénye. Az exponenciális eloszlást leggyakrabban véletlen időtartamok modellezésére használják. Részletes tárgyalása a Poisson folyamat című fejezetben található.

Egy alkatrész élettartama (jelölje T ) 1000 órákban mérve, exponenciális eloszlású 12 paraméterrel. Mennyi T 2 ?

Az exponenciális eloszlás kísérletében állítsuk be az r 12 paraméterértéket! Szimuláljunk 1000 kísérletet, és frissítsük az ábrát minden tizedik után. Figyeljük meg, hogyan konvergál az empirikus sűrűségfüggvény a valódi sűrűségfüggvényhez!

Véletlen szög

A Bertrand problémában egy bizonyos véletlen Θ szög valószínűségi sűrűségfüggvénye f θ θ ,  0 θ 2 .

  1. Igazoljuk, hogy f egy valószínűségi sűrűségfüggvény!
  2. Vázoljuk f gráfját, és határozzuk meg a móduszát!
  3. Mennyi Θ 4 ?

A Bertrand kísérletben tekintsük az egyenletes eloszlású távolság modelljét! Szimuláljunk 200 kísérletet, frissítsük az ábrát minden egyes kísérlet után, és határozzuk meg a Θ 4 esemény relatív gyakoriságát! Hasonlítsuk össze ezt az előző feladatban meghatározott valódi értékkel!

Gamma eloszlás

Legyen g n t t t n n ,  t 0 , ahol n paraméter.

  1. Igazoljuk, hogy g n egy valószínűségi sűrűségfüggvény minden n -re! Segítség: használjunk n -re vonatkozó indukciót!
  2. Igazoljuk, hogy g n t szigorúan monoton növekedő, amint t n , és szigorúan monoton csökkenő, amint t n , tehát t n a módusz.
  3. Vázoljuk g n gráfját!

Az előző, diszkrét eloszlásokról szóló részben beláttuk, hogy f t n g n t egy valószínűségi súlyfüggvény -en minden t 0 esetén. A g n sűrűségfüggvényű folytonos eloszlást pedig gamma eloszlásnak nevezzük, ahol n 1 az eloszlás paramétere. A gamma eloszlást részletesen a Poisson folyamat című fejezetben tárgyaljuk. Vegyük észre, hogy az n 0 eset épp az 1 paraméterű exponenciális eloszlást adja vissza.

Tegyük fel, hogy egy alkatrész élettartama, T , 1000 órákban mérve, n 2 paraméterű gamma eloszlású. Mennyi T 3 ?

A gamma eloszlás kísérletében állítsuk be az r 1 és a k 3 értékeket! Szimuláljunk 200 kísérletet (frissítsük az ábrát minden egyes kísérlet után) és határozzuk meg a T 3 esemény relatív gyakoriságát! Hasonlítsuk ezt össze az előző feladatban kapott elméleti valószínűség értékével!

Béta eloszlások

Legyen g x x 2 1 x ,  0 x 1 .

  1. Vázoljuk g gráfját!
  2. Határozzuk meg azt az f valószínűségi sűrűségfüggvényt, amely arányos g -vel (azaz csak egy konstans szorzóban tér el tőle)!
  3. Határozzuk meg a móduszt!
  4. Határozzuk meg 12 X 1 értékét, ahol X olyan valószínűségi változó, melynek sűrűsége a (b) pontban adott sűrűség!

Legyen g x 1 x 1 x ,  0 x 1 .

  1. Vázoljuk g gráfját!
  2. Határozzuk meg azt az f valószínűségi sűrűségfüggvényt, amely arányos g -vel (azaz csak egy konstans szorzóban tér el tőle)!
  3. Határozzuk meg 0 X 14 értékét, ahol X olyan valószínűségi változó, melynek sűrűsége a (b) pontban adott sűrűség!

Segítség: Az integrálásnál használjuk az u x helyettesítést!

Az előző két feladatban tekintett eloszlások béta eloszlások. A 13. feladat eloszlását arcus sinus eloszlásnak is nevezik. A béta eloszlásokat részletesen a Nevezetes eloszlások fejezetben tárgyaljuk.

A valószínűségi változók kísérletében válasszuk a béta eloszlást. A következő paraméterértékekre figyeljük meg a sűrűségfüggvény alakját! Szimuláljunk 1000 kísérletet (frissítsük az ábrát minden tizedik után), és figyeljük meg, hogyan konvergál az empirikus sűrűségfüggvény a valódi sűrűségfüggvényhez!

  1. a 3 , b 2 . Ez épp a 12. feladatban definiált béta eloszlás.
  2. a 12 , b 12 . Ez épp a 13. feladatban definiált arcus sinus eloszlás.

Pareto eloszlás

Legyen g x 1 x b ,  x 1 , ahol b 0 paraméter.

  1. Vázoljuk g gráfját!
  2. Igazoljuk, hogy 0 b 1 esetén nincs olyan valószínűségi sűrűségfüggvény, amely arányos lenne g -vel!
  3. Igazoljuk, hogy b 1 esetén a normáló konstans 1 b 1 .

Az előző feladatban definiált eloszlás a Pareto eloszlás, melyet Vilfredo Pareto-ról neveztek el. Ennek paramétere az a b 1 szám (így a paraméter pozitív). A Pareto eloszlás részletes tárgyalása a Nevezetes eloszlások fejezetben található.

Tegyük fel, hogy egy véletlenszerűen kiválasztott ember jövedelme, X , 3 paraméterű Pareto eloszlású. Mennyi X 2 ?

A valószínűségi változók kísérletében válasszuk ki az a 3 paraméterű Pareto eloszlást. Szimuláljunk 1000 kísérletet, és frissítsük az ábrát minden tizedik után. Határozzuk meg az X 2 esemény relatív gyakoriságát, és hasonlítsuk ezt össze az előző feladatban meghatározott elméleti valószínűséggel!

Cauchy eloszlás

Legyen g x 1 x 2 1 ,  x .

  1. Vázoljuk g gráfját!
  2. Igazoljuk, hogy a normáló konstans épp π.
  3. Határozzuk meg 1 X 1 értékét, ahol X sűrűségfüggvénye arányos g -vel!

Az előző feladatban definiált eloszlás az Augustin Cauchy-ról elnevezett Cauchy eloszlás (vagy más néven arcus tangens eloszlás). Ez az eloszlás a Student féle t eloszláscsalád tagja; a t eloszlások részletes tárgyalása a Nevezetes eloszlások fejezetben található. A g függvény gráfját néhol Agnesi boszorkányának nevezik Maria Agnesi tiszteletére.

A valószínűségi változók kísérletében válasszuk a Student féle t eloszlást. Állítsuk be az n 1 paraméterértéket, így megkapjuk a Cauchy eloszlást. Szimuláljunk 1000 kísérletet, frissítsük az ábrát minden tizediknél, és vizsgáljuk meg, hogyan konvergál az empirikus sűrűségfüggvény a valódi valószínűségi sűrűségfüggvényhez!

Standard normális eloszlás

Legyen g z 12 z 2 ,  z .

  1. Vázoljuk g gráfját!
  2. Igazoljuk, hogy a normáló konstans 2 . Segítség: jelölje c a normáló konstansot; fejezzük ki c 2 -et kettős integrállal, és térjünk át polár koordinátákra!

Az előző feladatban definiált eloszlás a standard normális eloszlás, ami talán a legfontosabb eloszlás a valószínűségszámításban. Normális eloszlással szokás közelíteni a fizikai kísérletekben fellépő hibákat. A normális eloszlások családját részletesen a Nevezetes eloszlások fejezetben tárgyaljuk.

A valószínűségi változók kísérletében válasszuk a normális eloszlást (az alapértelmezett beállítás ekkor a standard normális eloszlást adja). Szimuláljunk 1000 kísérletet, frissítsük az ábrát minden tizediknél, és vizsgáljuk meg, hogyan konvergál az empirikus sűrűségfüggvény a valódi valószínűségi sűrűségfüggvényhez!

Extrémérték eloszlás

Legyen f x x x , amint x .

  1. Igazoljuk, hogy f egy valószínűségi sűrűségfüggvény!
  2. Vázoljuk f gráfját, és határozzuk meg a móduszt! Figyeljük meg, mennyire nem szimmetrikus az eloszlás!
  3. Határozzuk meg X 0 értékét, ahol X valószínűségi sűrűségfüggvénye f .

Az előző feladatban definiált eloszlást nevezik 1. típusú extrémérték eloszlásnak, vagy Gumbel eloszlásnak (Emil Gumbel tiszteletére). Az extrémérték eloszlásokat részletesen a Nevezetes eloszlások fejezetben tárgyaljuk.

A valószínűségi változók kísérletében válasszuk ki az extrémérték eloszlást, és figyeljük meg a sűrűségfüggvény alakját! Szimuláljunk 1000 kísérletet, frissítsük az ábrát minden tizediknél, és vizsgáljuk meg, hogyan konvergál az empirikus sűrűségfüggvény a valódi valószínűségi sűrűségfüggvényhez!

További példák

Legyen f x x ,  0 x 1 .

  1. Vázoljuk f gráfját!
  2. Igazoljuk, hogy f egy valószínűségi sűrűségfüggvény!
  3. Határozzuk meg 13 X 12 értékét, ahol X valószínűségi sűrűségfüggvénye a (b)-beli függvény!

Legyen g x x 1 x ,  x 0 .

  1. Vázoljuk f gráfját!
  2. Határozzuk meg azt az f valószínűségi sűrűségfüggvényt, amely arányos g -vel, majd határozzuk meg ennek a móduszát!
  3. Határozzuk meg X 1 értékét, ahol X valószínűségi sűrűségfüggvénye a (b)-beli függvény!

Legyen f x y x y ,  0 x 1 ,  0 y 1 .

  1. Igazoljuk, hogy f egy valószínűségi sűrűségfüggvény!
  2. Határozzuk meg Y X értékét, ahol az X Y pár együttes sűrűségfüggvénye az (a)-beli függvény!
  3. Határozzuk meg X Y feltételes sűrűségét az X 12 Y 12 feltétel mellett!

Legyen g x y x y ,  0 x y 1 .

  1. Határozzuk meg azt az f valószínűségi sűrűségfüggvényt, amely arányos g -vel!
  2. Határozzuk meg Y 2 X értékét, ahol az X Y pár valószínűségi sűrűségfüggvénye az (a)-beli függvény!

Legyen g x y x 2 y ,  0 x 1 ,  0 y 1 .

  1. Határozzuk meg azt az f valószínűségi sűrűségfüggvényt, amely arányos g -vel!
  2. Határozzuk meg Y X értékét, ahol az X Y pár valószínűségi sűrűségfüggvénye az (a)-beli függvény!

Legyen g x y x 2 y ,  0 x y 1 .

  1. Határozzuk meg azt az f valószínűségi sűrűségfüggvényt, amely arányos g -vel!
  2. Határozzuk meg Y 2 X értékét, ahol az X Y pár valószínűségi sűrűségfüggvénye az (a)-beli függvény!

Legyen g x y z x 2 y 3 y ,  0 x 1 ,  0 y 1 ,  0 z 1 .

  1. Határozzuk meg azt az f valószínűségi sűrűségfüggvényt, amely arányos g -vel!
  2. Határozzuk meg X Y Z értékét, ahol az X Y Z hármas valószínűségi sűrűségfüggvénye az (a)-beli függvény!

Legyen g x y x y ,  0 x y .

  1. Határozzuk meg azt az f valószínűségi sűrűségfüggvényt, amely arányos g -vel!
  2. Határozzuk meg X Y 1 értékét, ahol az X Y pár valószínűségi sűrűségfüggvénye az (a)-beli függvény!

Folytonos egyenletes eloszlás

A következő feladat a folytonos eloszlások egy fontos osztályát írja le.

Tegyük fel, hogy S n , hogy 0 n S . Igazoljuk, hogy

  1. f x 1 n S ,  x S egy valószínűségi sűrűségfüggvényt definiál S -en!
  2. ha X sűrűsége az (a) pontban adott függvény, akkor X A n A n S ,  A S .

Azt az X valószínűségi változót, melynek a sűrűségfüggvénye a 32. feladatbeli függvény, S -en vett folytonos egyenletes eloszlásúnak nevezzük. A (b) feladatból következik, hogy S egy A részhalmazának valószínűsége az A szokásos (Lebesgue) mértékével arányos. Vegyük észre, hogy mind a diszkrét, mind a folytonos esetben egy X valószínűségi változó egyenletes eloszlású az S halmazon akkor és csak akkor, ha a súly-, vagy sűrűségfüggvénye konstans S -en. A síkbeli négyzeteken vett egyenletes eloszlású valószínűségi változók alapvető fontosságúak a Geometriai modelleknél.

Határozzuk meg X 0 Y 0 értékét az alábbi esetekben:

  1. X Y egyenletes eloszlású az S 6 6 2 négyzeten.
  2. X Y egyenletes eloszlású az S x y 6 y x 6 háromszögön.
  3. X Y egyenletes eloszlású az S x y x 2 y 2 36 körön.

A kétváltozós egyenletes eloszlás kísérletében válasszuk ki a következő tartományokat, majd szimuláljunk 100 kísérletet (frissítsük az ábrát minden kísérlet után)! Vizsgáljuk meg a kapott pontfelhőt! Határozzuk meg az X 0 Y 0 halmaz relatív gyakoriságát, és vessük ezt össze az előző feladatban meghatározott valódi valószínűséggel!

  1. Négyzet
  2. Háromszög
  3. Kör

Tegyük fel, hogy X Y Z egyenletes eloszlású az S 0 1 3 kockán. Mennyi X Y Z ?

  1. Határozzuk meg a fenti valószínűséget a valószínűségi sűrűségfüggvény segítségével!
  2. Határozzuk meg a fenti valószínűséget kombinatorikus okoskodással! Segítség: magyarázzuk meg, hogy X Y Z mind a 6 lehetséges rendezésének azonos a valószínűsége!

Egy bizonyos munka elvégzéséhez szükséges T idő (percekben mérve) egyenletes eloszlású a 15 60 intervallumon!

  1. Mennyi annak a valószínűsége, hogy a munka elvégzéséhez több mint 30 perc kell?
  2. Feltéve, hogy a munkát nem fejezték be 30 perc alatt, mi annak a valószínűsége, hogy még további 15 percre is szükség van?

Tegyük fel, hogy S n úgy, hogy 0 n S és B S , melyre n B 0 . Igazoljuk, hogy ha X egyenletes eloszlású S -en, akkor X feltételes eloszlása az X B feltétel mellett egyenletes B -n!

Adathalmaz elemzések

Ha adott egy D n adathalmaz az X folytonos eloszlású valószínűségi változó realizációról, akkor szerkeszthetünk egy empirikus sűrűségfüggvényt úgy, hogy az adathalmazunk értelmezési tartományát pici részhalmazokra bontjuk, majd minden kis részhalmazhoz hozzárendeljük a benne található pontok sűrűségét. Az empirikus sűrűségfüggvényeket részletesen a Véletlen minták című fejezetben tárgyaljuk.

A kabóca adathalmazban jelölje W B a testtömeget, L B a testhosszt és G a nemet. Határozzuk meg a következő valószínűségi változók empirikus sűrűségfüggvényét (és ábrázoljuk azokat) az adathalmaz alapján!

  1. W B
  2. L B
  3. W B feltéve, hogy G nőstény .

A kabóca adathalmazban jelölje L W a szárnyhosszt, W W pedig a szárnyszélességet. Határozzuk meg az L W W W pár empirikus sűrűségfüggvényét az adathalmaz alapján!

Elfajult folytonos eloszlások

A diszkrét esettel ellentétben a folytonos eloszlás sűrűségfüggvénye nem feltétlenül létezik, csak eddig feltettük a létezését. Előfordulhat, hogy egy S n halmazon értelmezett valószínűségi változónak nincs sűrűségfüggvénye; az ilyen eloszlást nevezzük elfajultnak, vagy degeneráltnak (néha pedig a sűrűségfüggvénnyel rendelkező eloszlásokat nevezik abszolút folytonos eloszlásoknak). Ebben a részben degenerált eloszlásokra nézünk fontos példákat.

Dimenziócsökkenés

Legyen X egy S n értékű valószínűségi változó, ahol n S 0 . Előfordulhat, hogy X folytonos eloszlású, de biztosan nincs n -re vonatkozó valószínűségi sűrűségfüggvénye. Ugyanis a definícióbeli (c) tulajdonság nem állhat fenn, mivel x A f x 0 tetszőleges f függvényre és A S részhalmazra. Mindazonáltal előfordulhat, hogy X alacsonyabb dimenziós, sűrűségfüggvénnyel rendelkező valószínűségi változókkal kifejezhető.

Például tegyük fel, hogy U egy folytonos eloszlású valószínűségi változó a T k halmazon, ahol k n , és X h U valamilyen folytonos, T -ből n -be képező h függvénnyel. Természetesen minden, X segítségével definiált esemény definiálható U -val is. A következő feladatban egy ilyen példát nézünk.

Tegyük fel, hogy Θ egyenletes eloszlású a 0 2 intervallumon. Legyen X Θ ,  Y Θ .

  1. Igazoljuk, hogy X Y folytonos eloszlású a C x y x 2 y 2 1 körön!
  2. Igazoljuk, hogy az X Y párnak nem létezik sűrűségfüggvénye C -n (a szokásos 2 , 2 -n értelmezett mértékre vonatkozólag)!
  3. Mennyi Y X ?

Keverék eloszlások

A sűrűségfüggvénnyel nem rendelkező folytonos eloszlásokra másik példa egy olyan X n -beli véletlen vektor ( n 1 ), amelynek néhány koordinátája diszkrét, néhány pedig folytonos eloszlású. Az ilyen, keverék eloszlásokkal a keverék eloszlásokról szóló részben foglalkozunk, azonban a következő feladatban is mutatunk egy példát.

Tegyük fel, hogy X egyenletes eloszlású a 0 1 2 halmazon, Y egyenletes eloszlású a 0 2 intervallumon, továbbá X és Y függetlenek.

  1. Igazoljuk, hogy X Y folytonos eloszlású az S 0 1 2 0 2 szorzathalmazon!
  2. Igazoljuk, hogy az X Y párnak nincs sűrűségfüggvénye az S halmazon (a szokásos 2 , 2 -n definiált mértékre nézve)!
  3. Mennyi Y X ?

Szinguláris folytonos eloszlások

Végül léteznek olyan folytonos eloszlások S n -en, ahol n S 0 , melyeknek mégsincs sűrűségfüggvényük. Az ilyen eloszlásokat (melyek a gyakorlatban elég ritkák) szinguláris eloszlásoknak nevezzük. Konstruáljunk egy ilyen eloszlást! Legyen X 1 X 2 Bernoulli kísérletek sorozata, ahol a siker valószínűsége p . A valószínűségi mérték p -től való függését úgy jelöljük, hogy p -t írunk az alsó indexbe. Tehát adott független indikátor változók egy sorozata, amelyre

p X i 1 p ,  p X i 0 1 p .

Gondoljunk X i -re úgy, mint az X , 0 1 értékű valószínűségi változó i -edik bináris jegyére (azaz kettes számrendszerbeli alakjának i -edik jegyére). Azaz

X i 1 X i 2 i .

Megfordítva, tudjuk, hogy minden x 0 1 szám felírható bináris alakban:

x i 1 x i 2 i  ahol  x i 0 1  amint   i 1 2 .

Ez a felírás egyértelmű azon esetek kivételével, amikor x bináris racionális, azaz x k 2 n alakú valamely k 1 2 2 n 1 számmal. Ez utóbbi esetben kétféle felírás létezik, az egyikben véges sok jegy után minden jegy nulla, a másiknál véges sok jegy után minden jegy egyes. Tekintsük definíció szerint ilyen esetekben a végtelen sok nullát tartalmazó felírást. Vegyük azonban észre, hogy a bináris racionális számok halmaza megszámlálható.

Igazoljuk, hogy X folytonos eloszlású, azaz p X x 0 minden x 0 1 esetén.

Most definiáljuk azon számok halmazát, ahol az egyesek relatív gyakoriságának határértéke p . Legyen

C p x 0 1 1 n i 1 n x i p  amint  n .

Igazoljuk, hogy

  1. C p C q amint p q .
  2. p X C p 1 , Segítség: használjuk a nagy számok erős törvényét.

Tehát azt kaptuk, hogy X lehetséges eloszlásai, amint p 0 és 1 között változik, kölcsönösen szingulárisak.

Tegyük fel, hogy p 12 . Igazoljuk, hogy X egyenletes eloszlású a 0 1 intervallumon! Azaz X eloszlása ebben az esetben a standard (Lebesgue) mérték 0 1 -en.

Az előző két feladat következménye, hogy ha p 12 , akkor X eloszlásának nincs sűrűségfüggvény (a szokásos, 0 1 -en értelmezett mértékre nézve). A fenti eredmények a gyakorlatban is alkalmazhatók, például egy ilyen alkalmazást láthatunk a Vörös és fekete nevű játékban játszható, úgynevezett merész stratégia leírásánál.

  1. Virtual Laboratories
  2. 2. Eloszlások
  3. 1
  4. 2
  5. 3
  6. 4
  7. 5
  8. 6
  9. 7
  10. 8