Kiindulási pontunk, mint általában, most is egy véletlen kísérlet a hozzá tartozó valószínűségi mezővel és az azon értelmezett valószínűségi mértékkel. Legyenek és a kísérletünktől függő valószínűségi változók úgy, hogy -értékű, pedig -értékű. Ekkor gondolhatunk úgy az párra, mint egy -értékű valószínűségi változóra. Ennek a fejezetnek az a célja, hogy megértsük, hogyan viszonyul eloszlása és külön-külön vett eloszlásaihoz. Ilyen esetben az eloszlását együttes eloszlásnak, és eloszlásait pedig marginális-, vagy peremeloszlásoknak nevezzük. Jegyezzük meg, hogy és külön-külön is lehetnek több dimenziósak.
Először is vegyük észre, hogy az együttes eloszlásból mindig megkaphatóak a peremeloszlások, azonban ez fordítva nem igaz!
Igazoljuk, hogy
Ha és függetlenek, akkor definíció szerint
és ahogy azt már korábban láttuk, a fenti valószínűségek ismerete egyértelműen meghatározza az pár eloszlását -n. Ha azonban és nem függetlenek, akkor együttes eloszlásukat nem lehet a marginális eloszlásokból meghatározni. Tehát általában az együttes eloszlás sokkal több információt tartalmaz, mint a peremeloszlások külön-külön.
A diszkrét esethez vegyük észre, hogy pontosan akkor megszámlálható, ha és megszámlálhatóak.
Tegyük fel, hogy diszkrét eloszlású az halmazon súlyfüggvénnyel. Igazoljuk, hogy súlyfüggvény az alábbi , és súlyfüggvénye az alábbi :
A folytonos esethez tegyük fel, hogy és , így
Legyen az pár folytonos eloszlású az halmazon, sűrűségfüggvénnyel. Igazoljuk, hogy sűrűségfüggvénye az alábbi , sűrűségfüggvénye pedig az alábbi :
A 2. és 3. feladatban szereplő függvényeket az pár együttes súly-, illetve sűrűségfüggvényének nevezzük, míg és az és változók marginális súly-, illetve sűrűségfüggvényei.
Ha a változók függetlenek, az együttes sűrűségfüggvény a peremsűrűségfüggvények szorzata.
Tegyük fel, hogy és függetlenek és vagy mindketten diszkrét, vagy mindketten folytonos eloszlásúak. Jelölje illetve az és változók súly-, vagy sűrűségfüggvényét. Igazoljuk, hogy az pár súly- vagy sűrűségfüggvényére:
A következő feladat a 4. feladat megfordítása: ha az együttes súly-, vagy sűrűségfüggvény felírható két függvény szorzataként, ahol az egyik függvény csak -től, a másik csak -tól függ, akkor és függetlenek.
Tegyük fel, hogy az pár diszkrét vagy folytonos eloszlású, súly-, vagy sűrűségfüggvénnyel. Tegyük fel továbbá, hogy
ahol és . Igazoljuk, hogy és függetlenek, és található egy nemnulla konstans, amellyel az változó súly-, vagy sűrűségfüggvénye, pedig az változó súly-, vagy sűrűségfüggvénye.
A most tárgyalt eredmények természetesen kiterjeszthetőek arra az esetre, amikor az pár koordinátái különböző eloszlás típusok, ahogy ezt a keverék eloszlásokról szóló fejezetben tárgyaltuk. Például tegyük fel, hogy diszkrét, pedig folytonos eloszlású, továbbá az pár együttes sűrűségfüggvénye (az halmazon) . Ekkor a 2.(a), a 3.(b), a 4. és az 5. feladatok eredménye érvényben marad.
Feldobtunk két hagyományos, igazságos kockát; a dobott értékeket az pár jelöli. Legyen és a dobott számok összege és különbsége.
Feldobtunk két hagyományos, igazságos kockát; a dobott értékeket az pár jelöli. Legyen a dobott számok minimuma, pedig a dobott számok maximuma.
Legyen az pár együttes sűrűségfüggvénye amint .
Legyen az pár együttes sűrűségfüggvénye amint .
Legyen az pár együttes sűrűségfüggvénye amint .
Legyen az pár együttes sűrűségfüggvénye amint .
Legyen az hármas együttes sűrűségfüggvénye amint .
Legyen az pár együttes sűrűségfüggvénye amint .
Elevenítsük fel, hogy mi is a standard (Lebesgue) mérték -en:
Speciálisan, a hosszt méri -en, a területet -n, pedig a térfogatot -n.
Tegyük fel, hogy egy , pedig egy értékű valószínűségi változó úgy, hogy az pár egyenletes eloszlású az halmazon. Ekkor definíció szerint együttes sűrűségfüggvénye:
Legyenek és projekciói (vagy más szóval vetületei) -re illetve -ra, azaz:
Ezután definiáljuk az és az pontban vett szeleteket:
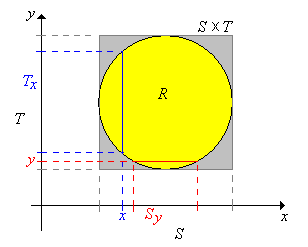
Igazoljuk, hogy az halmazban veszi fel az értékeit, és a sűrűségfüggvénye (melyet jelöljünk -vel) arányos a megfelelő szelet mértékével:
Igazoljuk, hogy a halmazban veszi fel az értékeit, és a sűrűségfüggvénye (melyet jelöljünk -val) arányos a megfelelő szelet mértékével:
Az előző két feladatból következik, hogy általában és se nem függetlenek, se nem egyenletes eloszlásúak.
Legyen . Igazoljuk, hogy
Az alábbi esetek mindegyikében határozzuk meg az együttes- és peremsűrűségeket, és döntsük el, hogy és függetlenek-e!
A kétváltozós egyenletes eloszlás kísérletében az alábbi alakzatok mindegyikére szimuláljunk 5000 kísérletet (és frissítsük az ábrát minden tizedik után)! Figyeljük meg a pontfelhő eloszlását, és az empirikus marginális eloszlásokat! Vessük össze a kísérleti ábrákat az előző feladatban kapott elméleti eredményekkel!
Tegyük fel, hogy egyenletes eloszlású a kockán.
Tegyük fel, hogy egyenletes eloszlású az halmazon.
A következő feladatból megtudhatjuk, hogyan állítható elő tetszőleges folytonos eloszlás egy darab egyenletes eloszlású valószínűségi változóból. Ez nagyon fontos lehet, ha valamilyen folytonos eloszlást szeretnénk szimulálni.
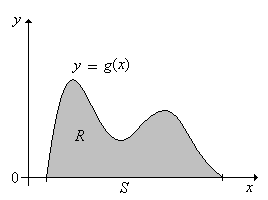
Tegyük fel, hogy egy halmazon értelmezett folytonos eloszlás sűrűségfüggvénye. Legyen
Igazoljuk, hogy ha egyenletes eloszlású -en, akkor sűrűségfüggvénye éppen . Az alábbi ábra az esetet ábrázolja:
Tegyük fel, hogy darab tárgyunk van, amelyek mindegyike négy különböző típusú lehet. Első típusú darab, második típusú darab, harmadik típusú darab és nulladik típusú darab. Az , és paraméterek természetesen nemnegatív egészek, továbbá . Véletlenszerűen, visszatevés nélkül kiválasztunk tárgyat. Jelölje a kiválasztott első, második és harmadik típusba tartozó tárgyak számát , és . Így a nulladik típusú tárgyakból darabot választottunk ki. Az alábbi feladatok ilyen esetekkel foglalkoznak, legyenek mindenütt az , , számok a halmaz elemei!
Kombinatorikus érvelésekkel igazoljuk, hogy (többváltozós) hipergeometrikus eloszlású, azaz a valószínűségi súlyfüggvénye:
Kombinatorikus és analitikus érvelésekkel is igazoljuk, hogy az pár (többváltozós) hipergeometrikus eloszlású az alábbi súlyfüggvénnyel. A kombinatorikus érvelésben tekintsünk a kísérletre úgy, mintha elemet választanánk egy elemű halmazból, ahol darab egyes típusú, darab kettes típusú, darab pedig valamilyen más típusú.
Kombinatorikus és analitikus érvelésekkel is igazoljuk, hogy az hipergeometrikus eloszlású a lenti súlyfüggvénnyel. A kombinatorikus érvelésben tekintsünk a kísérletre úgy, mintha elemet választanánk egy elemű halmazból, ahol darab egyes típusú, darab pedig valamilyen más típusú.
A fenti feladatok eredményei természetes módon általánosíthatóak több változó esetére. Így kapjuk, hogy egy hipergeometrikus eloszlású véletlen vektor komponenseinek tetszőleges részhalmaza is hipergeometrikus eloszlású. Más szóval, a hipergeometrikus eloszlás minden marginálisa is hipergeometrikus eloszlás. A hipergeometrikus eloszlásról és a többváltozós hipergeometrikus eloszlásról részletes leírást a Véges mintavételezési eljárások fejezetben olvashatunk.
Mint már korábban is tárgyaltuk, a bridzs kísérletben visszatevés nélkül választunk 13 lapot egy hagyományos, 52 lapos franciakártya pakliból. Legyen , és a kiválasztott pikkek, kőrök és kárók száma. Határozzuk meg az alábbi valószínűségi változók valószínűségi súlyfüggvényét:
Tekintsünk független kísérleteket, ahol minden kísérlet kimenetele négyféle lehet. Mindegyik kísérletnél az 1. kimenetel , a 2. kimenetel , a 3. kimenetel , a 0. kimenetel pedig valószínűséggel következik be. Természetesen a , és paraméterek olyan nemnegatív számok, hogy . Jelölje kísérlet során az 1 kimenetelű események számát , a 2 kimenetelek számát , a 3 kimenetelek számát pedig . Ekkor a 0. kimenetelek száma . Az alábbi feladatokban legyenek , és -beli számok.
Igazoljuk, hogy multinomiális (vagy polinomiális) eloszlású, azaz a súlyfüggvénye
aholValószínűségszámítási és analitikus érveléssel is igazoljuk, hogy is multinomiális eloszlású, méghozzá az alábbi súlyfüggvénnyel. A valószínűségszámítási érvelés lényegi része az az észrevétel, hogy a kísérletre tekinthetünk úgy, mint független kísérletre, ahol az 1. kimenetel valószínűsége mindig , a 2. kimenetelé , bármi más kimenetelé pedig .
Valószínűségszámítási és analitikus érveléssel is igazoljuk, hogy binomiális eloszlású, méghozzá az alábbi súlyfüggvénnyel. A valószínűségszámítási érvelés lényegi része az az észrevétel, hogy a kísérletre tekinthetünk úgy, mint független kísérletre, ahol az 1. kimenetel valószínűsége mindig , bármi más kimenetel valószínűsége pedig
Az eredmények természetes módon általánosíthatók olyan multinomiális kísérletekre, ahol tetszőleges számú kimenetel lehetséges. Ez esetben is igaz lesz, hogy egy multinomiális eloszlású vektor minden alacsonyabb dimenziós része is multinomiális eloszlású, azaz a multinomiális eloszlás marginálisai is multinomiálisak. A binomiális eloszlásról és a multinomiális eloszlásról részletesebben a Bernoulli kísérletekről szóló fejezetben olvashatunk.
Az egy-hat irányban lapos kocka egy olyan hatoldalú dobókocka, amelyet ha feldobnak, valószínűséggel mutat egyet vagy hatot, valószínűséggel pedig kettőt, hármat, négyet vagy ötöt. Feldobtunk egy ilyen kockát tízszer, és -vel jelöltük azt, hogy hányszor dobtuk az számot (). Határozzuk meg az alábbi valószínűségi változók súlyfüggvényét:
Legyen az valószínűségi változó pár sűrűségfüggvénye a következő:
Legyen az valószínűségi változó pár sűrűségfüggvénye a következő:
Az előző két példában adott együttes eloszlás a kétváltozós normális eloszlás speciális esetei. Normális eloszlást nagyon gyakran alkalmaznak a gyakorlatban, például hibával terhelt mérési eredmények modellezésére. A kétváltozós normális eloszlásról részletesen a Nevezetes eloszlások fejezetben olvashatunk.
Az exponenciális eloszlás sűrűségfüggvénye a következő
ahol a ráta paraméter. Az exponenciális eloszlást leggyakrabban érkezési idők modellezésére használják, részletesebben lásd a Poisson folyamat fejezetet.
Legyenek és , illetve paraméterű, független exponenciális eloszlású változók. Igazoljuk, hogy
Legyenek , és , és paraméterű, független exponenciális eloszlású változók. Igazoljuk, hogy
Ha , és függetlenül működő berendezések élettartamai, akkor a tönkremeneteli sorrendjük az előző feladatokban kapott képletekkel írható le. Ezek az eredmények a folytonos idejű Markov láncok elméletében is nagyon fontosak, erről részletesen a valószínűségi változók transzformáltjairól szóló részben olvashatunk.
Legyen egy -értékű, pedig egy -értékű valószínűségi változó, melyek együttes sűrűségfüggvénye:
Legyen egy -értékű, pedig egy -értékű valószínűségi változó, melyek együttes sűrűségfüggvénye:
Ahogy a feltételes eloszlásról szóló részben látni fogjuk, az utóbbi feladatban megadott eloszlás az alábbi kísérlettel állítható elő: válasszunk egy véletlentől függő értéket, majd dobjunk fel háromszor egy olyan pénzérmét, amely valószínűséggel mutat fejet. Jelölje a dobott fejek számát.
A kabóca adathalmazban jelölje a nemet, pedig az alfajt.
A kabóca adathalmazban jelölje a testtömeget, pedig a testhosszt.
A kabóca adathalmazban jelölje a nemet, pedig a testtömeget.