Kovariancia és korreláció

A bevezetőben említettük, hogy egy valószínűségi változó különböző függvényeinek várható értéke révén a valószínűségi változó sok fontos tulajdonságát jellemezhetjük. Ebben a fejezetben olyan várható értékeket fogunk vizsgálni, melyekkel két valószínűségi változó egymáshoz való viszonyát írjuk majd le. Ez a viszony rendkívül fontos mind a valószínűségszámításban, mint a statisztikában.

Általános elmélet

Definíciók

és (feltéve, hogy a szórásnégyzetek pozitívak),

X

és

Y

korrelációja:

A korreláció a kovariancia skálázott változata. Vegyük észre, hogy a két mennyiségnek mindig azonos az előjele (pozitív, negatív, vagy 0). Ha az előjel pozitív, azt mondjuk, hogy a változók pozitívan korreláltak, ha negatív, negatívan korreláltak, ha 0, korrelálatlanok. Vegyük észre továbbá, hogy a korreláció dimenzió nélküli mérőszám, hisz a számláló és a nevező mértékegysége megegyezik.

Ahogy a neve sugallhatja, a kovariancia és a korreláció a valószínűségi változók közötti függőséget méri. Célunk most ezt a függőséget jól megérteni. Vegyük észre, hogy

X Y

X Y

, együttes eloszlásának középpontja, továbbá az ezen a ponton átmenő vízszintes és függőleges egyenes

2

-et négy részre osztja. A

x y x X y Y

függvény ezek közül a síknegyedek közül az elsőn és a harmadikon pozitív, a másodikon és a negyediken negatív.

Tulajdonságok

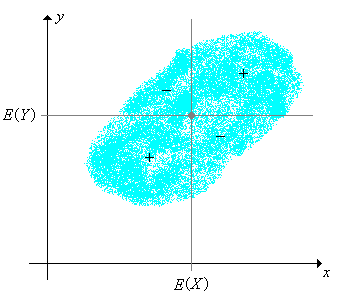
A következő feladatok a kovariancia alapvető tulajdonságaira világítanak rá. Megoldásukhoz lényeges tudni, hogy egy valószínűségi változó lineáris függvényének várható értékét hogyan számítjuk ki. A kovariancia más érdekes tulajdonságait a legjobb lineáris becslőről szóló részben fogjuk megismerni.

Igazoljuk, hogy $X Y X Y X Y$ .

Az 1. feladat alapján

X

és

Y

akkor és csak akkor korrelálatlanok, ha

X Y X Y

. Speciálisan, ha

X

és

Y

függetlenek, akkor korrelálatlanok. Az állítás megfordítása viszont nem igaz, ahogy azt a következő feladat is demonstrálja. (Még több ilyen példát fogunk látni a számolási feladatoknál.)

Tegyük fel, hogy $X$ egyenletes eloszlású az $a a$ intervallumon, ahol $a 0$ és $Y X 2$ Igazoljuk, hogy $X$ és $Y$ korrelálatlanok, miközben $Y$ az $X$ függvénye (azaz nemcsak hogy nem függetlenek, de a lehető legszorosabb köztük a függőség).

Igazoljuk, hogy $X Y Y X$ .

Igazoljuk, hogy $X X X$ . Tehát a szórásnégyzet a kovariancia speciális esete.

Igazoljuk, hogy $X a Y b X Y$ .

Igazoljuk, hogy $a X b Y Z a X Z b Y Z .$

Tehát ha a második változót fixen hagyjuk, a kovariancia lineáris az első változójában. A szimmetria miatt ez fordítva is igaz: ha az első változót fixen hagyjuk, lineáris a második változójában. Tehát a kovariancia operátor bi-lineáris. Ennek a tulajdonságnak az általános megfogalmazása a következő feladat:

Tegyük fel, hogy $X 1 X 2 X n$ és $Y 1 Y 2 Y m$ valós értékű valószínűségi változók sorozatai. Igazoljuk, hogy

i 1 n a i X i j 1 m b j Y j i 1 n j 1 m a i b j X i Y j .

Igazoljuk, hogy $X$ és $Y$ korrelációja megegyezik a standardizáltjaik korrelációjával:

X Y X X 𝔻 X Y Y 𝔻 Y .

Összeg szórásnégyzete

Belátjuk, hogy valószínűségi változók összegének szórásnégyzete épp a páronként vett kovarianciák összege. Ez azért is fontos eredmény, hisz sok nevezetes eloszlást felírhatunk egyszerűbb eloszlású valószínűségi változók összegeként (lásd például a binomiális eloszlást, vagy a hipergeometriai eloszlást).

Tegyük fel, hogy $X 1 X 2 X n$ valós értékű valószínűségi változók sorozata. A 3. feladat, 4. feladat és a 6. feladat segítségével igazoljuk, hogy

i 1 n X i i 1 n j 1 n X i X j i 1 n X i 2 i j X i X j .

Vegyük észre, hogy az összeg varianciája lehet kisebb, nagyobb, vagy egyenlő az varianciák összegével. A 9. feladat speciális eseteként, ha

n 2

, akkor

Tegyük fel, hogy $X 1 X 2 X n$ páronként korrelálatlan valós értékű valószínűségi változók sorozata. Igazoljuk, hogy

i 1 n X i i 1 n X i .

Vegyük észre, hogy az előző feladat alkalmazható arra a speciális esetre, amikor a valószínűségi változók páronként függetlenek.

Legyenek $X$ és $Y$ valós értékű valószínűségi változók. Igazoljuk, hogy $X Y X Y 2 X 2 Y$ .

Tegyük fel, hogy $X$ és $Y$ valós értékű valószínűségi változók, továbbá $X Y$ . Igazoljuk, hogy $X Y$ és $X Y$ korrelálatlanok.

Véletlen minták

A következő feladatokban legyen

X 1 X 2

független, azonos eloszlású valós értékű valószínűségi változók sorozata, melyeknek közös várható értékük

μ,

szórásuk

σ 0

. (Azaz, a változók egy közös eloszlásból származó véletlen mintát alkotnak).

Legyen $Y n i 1 n X i$ . Igazoljuk, hogy

$Y n n μ,$
$Y n n σ 2 .$

Legyen $M n Y n n 1 n i 1 n X i$ . Azaz $M n$ a mintaátlag. Igazoljuk, hogy

$M n μ,$
$M n M n μ 2 σ 2 n$ , tehát $M n 0$ amint $n,$
$M n μ ε 0$ amint $n$ bármely $ε 0$ esetén. (Segítség: használjuk a Csebisev egyenlőtlenséget.)

Legyen $Z n Y n n μ n σ$ , azaz $Z n$ $Y n$ standardizáltja. Igazoljuk, hogy

$Z n M n μ σ n,$ tehát $Z n$ az $M n$ valószínűségi változó standardizáltja is egyben,
$Z n 0,$
$Z n 1 .$

A centrális határeloszlás-tétel, a valószínűségszámítás másik fontos alaptétele azt állítja, hogy

Z n

eloszlása, amint

n,

tart a normális eloszláshoz.

Véletlen események

Legyenek

A

és

B

egy kísérlethez tartozó események. Ekkor

A

és

B

kovarianciája és korrelációja definíció szerint az

A,

B

indikátor valószínűségi változóik kovarianciája, illetve korrelációja.

Igazoljuk, hogy

$A B A B A B,$
$A B A B A B A 1 A B 1 B .$

Speciálisan

A

és

B

pozitívan korreláltak/negatívan korreláltak/függetlenek (a feltételes valószínűségről szóló fejezetben lévő definíció értelmében) pontosan akkor, ha

A

illetve

B

indikátor valószínűségi változóik pozitívan korreláltak/negatívan korreláltak/korrelálatlanok.

Igazoljuk, hogy

$A B A B,$
$A B A B .$

Tegyük fel, hogy $A B .$ Igazoljuk, hogy

$A B A 1 B,$
$A B A 1 B B 1 A .$

A legjobb lineáris becslő

Vajon

X

melyik lineáris függvénye van a legközelebb

Y

-hoz abban az értelemben, hogy mikor a legkisebb a négyzetes hiba? Akkor rendkívül fontos ez a kérdés, ha az

X

valószínűségi változó megfigyelhető (úgynevezett magyarázó változó), az

Y

viszont nem (úgynevezett magyarázott változó). A lineáris függvényünkkel ez esetben a megfigyelt

X

értékből becsüljük

Y

értékét. A megfelelő lineáris függvény megtalálása során megfigyelhetjük, hogy a kovariancia és a korreláció valójában az

X

és

Y

közötti lineáris kapcsolatot méri. A triviális eseteket zárjuk ki, azaz tegyük fel, hogy

X 0

és

Y 0

, vagyis a valószínűségi változóink valóban függnek a véletlentől.

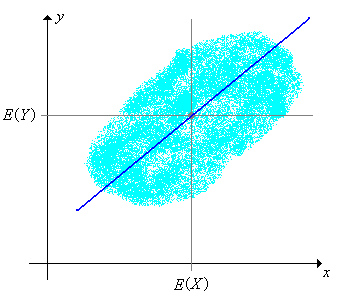
Jelölje

MSE a b

az átlagos négyzetes hibát, amikor az

a X b

lineáris kifejezéssel közelítjük

Y

értékét. (Az MSE a mean square error angol kifejezés rövidítése.) Ez az

a

és a

b

paraméterek függvénye:

Igazoljuk, hogy

MSE a b Y 2 2 a X Y 2 b Y a 2 X 2 2 a b X b 2 .

Igazoljuk, hogy $MSE a b$ akkor minimális, ha

a X Y X, b Y X Y X X .

Tehát

Y

legjobb lineáris becslője

X

ismeretében az

L Y X

valószínűségi változó, ahol

Igazoljuk, hogy az MSE átlagos négyzetes hibafüggvény minimuma

Y L Y X 2 Y 1 X Y 2 .

Az előző feladatot felhasználva igazoljuk a következő fontos tulajdonságokat:

$1 X Y 1,$
$𝔻 X 𝔻 Y X Y 𝔻 X 𝔻 Y,$
$X Y 1$ pontosan akkor, ha $Y a X b$ majdnem biztosan, valamilyen $a 0$ és $b$ konstansokkal,
$X Y 1$ pontosan akkor, ha $Y a X b$ majdnem biztosan, valamilyen $a 0$ és $b$ konstansokkal.

Az előző feladatok világosan mutatják, hogy

X Y

és

X Y

X

és

Y

közötti lineáris kapcsolatot mérik.

Nyilván

Y

legjobb konstans becslése, azaz, amikor minimális az átlagos négyzetes hiba, épp

Y

és ekkor az átlagos négyzetes hiba értéke

Y

. Tehát az

Y

szórásnégyzete és a 21. feladat-ban kapott legkisebb négyzetes hiba közti különbség az a mennyiség, amennyivel csökken az

Y

bizonytalansága, ha a becslőnkben megjelenhet egy

X

-ben lineáris tag.

Igazoljuk, hogy $Y Y L Y X 2 Y X Y 2$ A szórásnégyzet relatív csökkenése $X Y 2$ , ezért ezt a mennyiséget úgy hívják, hogy meghatározottsági együttható.

A fenti jelöléssel az

x L Y X x

függvényt

Y

X

-re vonatkozó lineáris regressziós függvényének nevezzük, a függvény grafikonja pedig a regressziós egyenes. Vegyük észre, hogy a regressziós egyenes illeszkedik az

X Y

pontra, azaz az együttes eloszlás középpontjára.

Igazoljuk, hogy $L Y X Y$ .

A magyarázó és a magyarázott változók szerepe triviálisan nem cserélhető fel, erre a jelenségre világít rá a következő feladat.

Igazoljuk, hogy $Y$ $X$ -re vonatkozó regressziós egyenese és $X$ $Y$ -ra vonatkozó regressziós egyenese általában nem esik egybe, kivéve a triviális esetet, azaz amikor a két változó maximálisan korrelált. A meghatározottsági együttható viszont független attól, hogy melyik változó a függő és melyik a független.

Legyenek $A$ és $B$ véletlen események, továbbá $0 A 1$ és $0 B 1$ . Igazoljuk, hogy

$A B 1$ akkor és csak akkor, ha $A B 0$ és $B A 0 .$ (Azaz $A$ és $B$ ekvivalensek.)
$A B 1$ akkor és csak akkor, ha $A B 0$ és $B A 0 .$ (Azaz $A$ és $B$ ekvivalensek.)

A legjobb lineáris becslő még annál is hasznosabb, mint amilyennek az eddig elmondottak alapján tűnik. Ugyanis nemcsak az eredeti valószínűségi változókra, hanem azok transzformáltjaira is alkalmazhatjuk az eddigieket. Tegyük fel, hogy

X

és

Y

S

, illetve

T

értékű valószínűségi változók. Legyenek továbbá

g

és

h

valós értékű függvények, melyek értelmezési tartománya

S

illetve

T

. Ekkor meghatározhatjuk

L h Y g X

-et, azaz

g X

azon lineáris függvényét, amely a legközelebb van

h Y

-hoz olyan értelemben, hogy minimális az átlagos négyzetes hiba. Természetesen az eddigi eredményeink alkalmazhatók arra az esetre is, amikor

X

helyett

g X

Y

helyett

h Y

szerepel.

Tegyük fel, hogy $Z$ egy valós értékű valószínűségi változó, $c$ pedig konstans. Igazoljuk, hogy

$L Y Z X L Y X L Z X,$
$L c Y X c L Y X .$

Példák és alkalmazások

Egyenletes eloszlás

Legyen az $X Y$ pár egyenletes eloszlású az $S 2$ halmazon. Határozzuk meg $X Y$ -t és $X Y$ -t, és döntsük el, hogy függetlenek-e a változók a következő esetekben:

$S a b c d$ , ahol $a b$ és $c d,$
$S x y 2 a y x a$ , ahol $a 0$ ,
$S x y 2 x 2 y 2 r 2$ , ahol $r 0$ .

A kétdimenziós egyenletes eloszlás kísérletében válasszuk ki az alábbi halmazokat. Minden halmazra szimuláljunk 2000 kísérletet (frissítsük az ábrát minden 10. után), és figyeljük meg, hogyan változik a korreláció értéke és a pontfelhő alakja. Hasonlítsuk ezt össze az előző feladat eredményével.

Négyzet
Háromszög
Kör

Tegyük fel, hogy $X$ egyenletes eloszlású a $01$ intervallumon, és ha $X x$ , akkor $Y$ egyenletes eloszlású $0 x$ -en.

Mennyi $X Y$ ?
Mennyi $X Y$ ?
Mivel egyenlő $L Y X$ ?
Mivel egyenlő $L X Y$ ?

Kockadobások

Egy hagyományos kocka alatt hat oldalú dobókockát értünk. Az igazságos kocka olyan, hogy ha feldobjuk, minden oldalára azonos valószínűséggel esik. Az egy-hat irányban lapos kocka egy hagyományos kocka, ami feldobás után az 1 és 6 értékeket

1 4

, a 2, 3, 4 és 5 értékeket

1 8

valószínűséggel mutatja.

Két igazságos kockát feldobtunk, a dobott értékeket az $X 1 X 2$ pár jelöli. Legyen $Y X 1 X 2$ a dobott számok összege, $U X 1 X 2$ a kisebbik dobott szám, $V X 1 X 2$ a nagyobbik dobott szám. Határozzuk meg a következő valószínűségi változó párok kovarianciáját és korrelációját:

$X 1 X 2,$
$X 1 Y,$
$X 1 U,$
$U V,$
$U Y .$

Tegyük fel, hogy most $n$ db igazságos kockát dobtunk fel. Határozzuk meg a következő valószínűségi változók várható értékét és varianciáját:

A dobott számok összege,
A dobott számok átlaga.

A kockadobálós kísérletben válasszuk ki a következő valószínűségi változókat. Minden esetben növeljük a kockák számát, és figyeljük meg, hogyan változik a várható értéket és a szórást jelölő intervallum. $n 20$ paraméterválasztással szimuláljunk 1000 kísérletet (frissítsük az ábrát minden tizedik után), és figyeljük meg, hogyan konvergálnak az empirikus momentumok a valódi momentumokhoz.

A dobott számok összeg,
A dobott számok átlaga.

Oldjuk meg a 32. feladatot egy-hat irányban lapos kockával.

Oldjuk meg a 33. feladatot egy-hat irányban lapos kockával.

Két igazságos kockát feldobtunk, a dobott értékeket az $X 1 X 2$ pár jelöli. Legyen $Y X 1 X 2$ a dobott számok összege, $U X 1 X 2$ a nagyobbik dobott szám, $V X 1 X 2$ a kisebbik dobott szám. Határozzuk meg a következőket:

$L Y X 1,$
$L U X 1,$
$L V X 1$ .

Bernoulli kísérletek

A Bernoulli kísérletek folyamata egy

X 1 X 2

független, azonos eloszlású indikátor valószínűségi változókból álló sorozat. Megbízhatóság-elméleti kifejezéssel élve

X i

jelöli az

i

-edik kísérlet eredményét, ahol 1-et írunk, ha sikeres volt a kísérlet és 0-t, ha sikertelen. A siker valószínűsége

p X i 1,

ez a folyamat paramétere. Nevét James Bernoulli-ról kapta. A folyamat részletes tárgyalása a Bernoulli kísérletek fejezetben található.

Az első

n

kísérletből a sikeresek száma

Y n i 1 n X i

. Ez a valószínűségi változó

n

és

p

paraméterű binomiális eloszlású, melynek valószínűségi súlyfüggvénye

Igazoljuk, hogy

$Y n n p,$
$Y n n p 1 p .$

A binomiális érmedobás kísérletben válasszuk a fejek számát. Változtassuk az $n$ és $p$ paraméter értékeit, és figyeljük meg, hogyan változik a várható értéket és a szórást jelölő intervallum. Néhány $n$ és $p$ paraméterpárral szimuláljunk 1000 kísérletet (frissítsük az ábrát minden tizedik után), és figyeljük meg, hogyan konvergál az empirikus várható érték és szórás a valódi várható értékhez és szóráshoz.

Az első

n

kísérlet során a sikeresek aránya

M n Y n n

. Ezt a valószínűségi változót nevezik a

p

paraméter statisztikai becslőjének.

Igazoljuk, hogy

$M n p,$
$M n p 1 p n .$

A binomiális érmedobás kísérletében válasszuk a fejek arányát. Változtassuk az $n$ és $p$ paraméterértékeket, és figyeljük meg, hogyan változik a várható értéket és a szórást jelölő intervallum. Néhány $n$ és $p$ paraméterpárral szimuláljunk 1000 kísérletet (frissítsük az ábrát minden tizedik után), és figyeljük meg, hogyan konvergál az empirikus várható érték és szórás a valódi várható értékhez és szóráshoz.

Hipergeometriai eloszlás

Tegyük fel, hogy egy populáció

m

egyedből áll, ezek közül

r

darab 1-es típusú,

m r

darab pedig 0-ás típusú. Visszatevés nélkül kiválasztunk

n

véletlen egyedet. Legyen

X i

i

-edik kiválasztott egyed típusa. Ekkor tudjuk, hogy

X 1 X 2 X n

azonos eloszlású valószínűségi változók, melyek azonban nem függetlenek. Valójában ez a valószínűségi változó sorozat felcserélhető, tehát például

X i 1 r m

minden

i

-re és

X i 1 X j 1 r m r 1 m 1

minden különböző

i

-re és

j

-re.

Jelölje

Y n

a mintában előforduló 1-es típusú egyedek számát, azaz

Y n i 1 n X i .

Ekkor ez a valószínűségi változó hipergeometriai eloszlású, és valószínűségi súlyfüggvénye:

Igazoljuk, hogy különböző $i$ -re és $j$ -re

$X i X j r m 1 r m 1 m 1,$
$X i X j 1 m 1 .$

Vegyük észre, hogy az az esemény, hogy az

i

-edik húzásra 1-es típusú egyedet választunk, illetve hogy a

j

-edik húzásra 1-es típusú egyedet választunk, negatívan korreláltak, de a korreláció nem függ az 1-es típusú egyedek számától, csak a populáció létszámától. Vegyük továbbá észre, hogy a korreláció maximális, ha

m 2

. Meg tudjuk ezt intuitívan magyarázni?

Igazoljuk, hogy

$Y n n r m,$
$Y n n r m 1 r m m n m 1 .$

A golyók és urnák kísérletben válasszunk visszatevés nélküli mintavételt. Változtassuk $m$ , $r$ és $n$ értékét, és figyeljük meg, hogyan változik súlyfüggvény alakja, valamint a várható értéket és a szórást jelölő intervallum. Néhány fix paraméterválasztással szimuláljunk 1000 kísérletet (frissítsük az ábrát minden tizedik után), és figyeljük meg, hogyan konvergál az empirikus várható érték és szórás a valódi várható értékhez és szóráshoz.

Vegyes feladatok

Legyenek $X$ és $Y$ valós értékű valószínűségi változók, és legyen $X Y 3$ . Mennyi $2 X 5 4 Y 2$ ?

Legyenek $X$ és $Y$ valós értékű valószínűségi változók, továbbá $X 5$ , $Y 9$ és $X Y 3$ . Mennyi $2 X 3 Y 7$ ?

Tegyük fel, hogy $X$ és $Y$ független, valós értékű valószínűségi változók, továbbá $X 6$ és $Y 8$ . Mennyi $3 X 4 Y 5$ ?

Legyenek $A$ és $B$ események, továbbá $A 1 2$ , $B 1 3$ , és $A B 1 8$ . Határozzuk meg $A$ és $B$ kovarianciáját és korrelációját!

Legyen az $X Y$ valószínűségi változó pár együttes sűrűségfüggvénye $f x y x y, 0 x 1, 0 y 1$ .

Mennyi $X Y$ ?
Mennyi $X Y$ ?
Határozzuk meg $L Y X$ -t!
Határozzuk meg $L X Y$ -t!

Legyen az $X Y$ valószínűségi változó pár együttes sűrűségfüggvénye $f x y 2 x y, 0 x y 1$ .

Mennyi $X Y$ ?
Mennyi $X Y$ ?
Határozzuk meg $L Y X$ -t!
Határozzuk meg $L X Y$ -t!

Legyen az $X Y$ valószínűségi változó pár együttes sűrűségfüggvénye $f x y 2 x y, 0 x y 1$ .

Mennyi $X 2 Y$ ?
Mennyi $X 2 Y$ ?
Határozzuk meg $L Y X 2$ -t!
Melyik $Y$ jobb lineáris becslője: amelyik $X$ alapján, vagy amelyik $X 2$ alapján becsli $Y$ -t?

Legyen az $X Y$ valószínűségi változó pár együttes sűrűségfüggvénye $f x y 6 x 2 y, 0 x 1, 0 y 1$ .

Mennyi $X Y$ ?
Mennyi $X Y$ ?
Határozzuk meg $L Y X$ -et!
Határozzuk meg $L X Y$ -et!

Legyen az $X Y$ valószínűségi változó pár együttes sűrűségfüggvénye $f x y 15 x 2 y, 0 x y 1$ .

Mennyi $X Y$ ?
Mennyi $X Y$ ?
Határozzuk meg $L Y X$ -t!
Határozzuk meg $L X Y$ -t!

Legyen az $X Y$ valószínűségi változó pár együttes sűrűségfüggvénye $f x y 15 x 2 y, 0 x y 1$ .

Mennyi $X Y$ ?
Mennyi $X Y$ ?
Határozzuk meg $L Y X$ -t!
Melyik $Y$ jobb lineáris becslője: amelyik $X$ alapján, vagy amelyik $X$ alapján becsli $Y$ -t?

Alapfogalmak a vektorterek elméletéből

A kovariancia a vektorterek elméletében a skaláris, vagy belső szorzatnak felel meg. Hasznos, ha megértjük ezt a definíciót is, ugyanis ha egy másik szemszögből is megvizsgáljuk ugyanazt a fogalmat, akkor jobban megérthetjük a jelenségeket.

Ebben a fejezetben a

V 2

vektortér az olyan

Ω F

valószínűségi mezőn értelmezett valós értékű valószínűségi változókból áll, melyeknek véges a második momentumuk. Két valószínűségi változót ekvivalensnek nevezünk, ha 1 valószínűséggel megegyeznek. Két ilyen valószínűségi változóhoz rendeljük ugyanazt a vektort, így precízen a vektorterünk a fenti ekvivalencia reláció szerinti ekvivalencia osztályokból áll. Az összeadás legyen a valószínűségi változók, mint függvények összeadása, a skalárral való szorzás pedig a valószínűségi változó, mint függvény, adott (determinisztikus) számmal való szorzása.

Belső szorzat

X

és

Y

V 2

-beli valószínűségi változók, akkor definiálhatjuk a belső szorzatukat (vagy skaláris szorzatukat) a következő módon:

A következő feladatban a már korábban bizonyított kovariancia alaptulajdonságainak megfelelő állításokat bizonyíthatjuk be, és egyúttal azt is belátjuk, hogy a fenti definíció valóban egy belső szorzat.

Igazoljuk, hogy

$X Y Y X,$
$X X 0,$
$X X 0$ pontosan akkor, ha $X 0 1$ (azaz ha $X$ ekvivalens a 0-val),
$a X Y a X Y$ tetszőleges $a$ konstanssal,
$X Y Z X Z Y Z .$

Ezzel a belső szorzattal könnyen definiálható a kovariancia és a korreláció. Két valószínűségi változókovarianciája ugyanis nem más, mint a centrált változatuk belső szorzata, korrelációja pedig épp a standardizáltjuk belső szorzata.

Igazoljuk, hogy

$X Y X X Y Y,$
$X Y X X 𝔻 X Y Y 𝔻 Y .$

A fenti belső szorzatból származó norma épp az átlagos négyzetes távolság. Egyedül a 2-norma származik belső szorzatból az összes

k

-norma közül, ezért is olyan fontos az átlagos négyzetes távolság mind a valószínűségszámításban, mind a statisztikában.

Igazoljuk, hogy $X X X 2 2 X 2$ .

Projekció

Igazoljuk, hogy a következő halmaz $V 2$ altere. Ezt a halmazt úgy is hívják, hogy az $X$ és az 1 elemek által generált altér:

W a X b a és b .

Igazoljuk, hogy $X$ ismeretében $Y$ legjobb lineáris becslője nem más, mint $Y$ -nak a $W$ altérre vett projekciója (vagy vetítése). Vagyis lássuk be, hogy $L Y X$ az egyetlen olyan $W W$ valószínűségi változó, hogy $Y W$ merőleges $W$ -re. Ezt úgy láthatjuk be, hogy olyan $W$ vektort keresünk, amely kielégíti a következő két egyenletet:

$Y W X 0,$
$Y W 1 0 .$

Hölder egyenlőtlenség

A következő feladatban a Hölder egyenlőtlenséget látjuk be (amely nevét Otto Hölder-ről kapta).

Tegyük fel, hogy $j 1$ , $k 1$ , és $1 j 1 k 1$ . Az alábbi lépéseket követve lássuk be, hogy $X Y X j Y k$ :

Igazoljuk, hogy $S x y 2 x 0 y 0$ konvex halmaz és $g x y x 1 j y 1 k$ konkáv $S$ -en.
Az (a) pont eredménye és a Jensen egyenlőtlenség segítségével lássuk be, hogy ha $U$ és $V$ nemnegatív valószínűségi változók, akkor $U 1 j V 1 k U 1 j V 1 k .$
Alkalmazzuk a (b) pont eredményét $U X j$ és $V Y k$ választással.

Az előző feladatban szereplő

j

és

k

értékeket konjugált exponenseknek nevezik. Ha a

j k 2

speciális esetet tekintjük, visszakapjuk a Cauchy-Schwarz egyenlőtlenséget (nevét Augustin Cauchy-ről és Karl Schwarz-ról kapta). Ez utóbbi ekvivalens a 22. feladatban bizonyított egyenlőtlenséggel.

Legyen az $X Y$ valószínűségi változó pár együttes sűrűségfüggvénye $f x y x y, 0 x 1, 0 y 1$ . Igazoljuk a Hölder egyenlőtlenséget a következő esetekben:

$j k 2,$
$j 3, k 3 2 .$

Tegyük fel, hogy $j$ és $k$ konjugált exponensek.

Igazoljuk, hogy $k j j 1$ .
Igazoljuk, hogy $k 1,$ amint $j$

További tételek

Igazoljuk a paralelogramma szabályt:

X Y 2 2 X Y 2 2 2 X 2 2 2 Y 2 2 .

Bizonyítsuk be a Pitagorasz tételt (amely a nevét természetesen Pythagoras-ról kapta): ha $X 1 X 2 X n$ egy olyan valós értékű valószínűségi változókból álló sorozat, hogy $X i X j 0,$ ha $i j,$ akkor

i 1 n X i 2 2 i 1 n X i 2 2 .

3. Kovariancia és korreláció

Általános elmélet

Definíciók

Tulajdonságok

Összeg szórásnégyzete

Véletlen minták

Véletlen események

A legjobb lineáris becslő

Példák és alkalmazások

Egyenletes eloszlás

Kockadobások

Bernoulli kísérletek

Hipergeometriai eloszlás

Vegyes feladatok

Alapfogalmak a vektorterek elméletéből

Belső szorzat

Projekció

Hölder egyenlőtlenség

További tételek