A várható érték a valószínűségszámítás egyik legfontosabb fogalma. Egy valós értékű valószínűségi változó várható értéke bizonyos értelemben az eloszlásának középpontját határozza meg. Továbbá a változó különböző valós transzformáltjai várható értékének meghatározása által az eloszlás egy sor érdekes tulajdonságára (mennyire elkent az eloszlás, mennyire szimmetrikus, stb.) következtethetünk. Bizonyos értelemben azt mondhatjuk, a várható érték általánosabb fogalom, mint maga a valószínűség.
Tekintsünk egy véletlen kísérletet egy valószínűségi mértékkel ellátott valószínűségi mezőn. Tegyük fel, hogy egy
értékű, a véletlen kísérlettől függő valószínűségi változó.Ha diszkrét eloszlású súlyfüggvénnyel (azaz megszámlálható), akkor várható értéke legyen
feltéve, hogy a fenti szumma abszolút konvergens (azaz, ha a képletben -et -re cseréljük, véges értéket kapunk). Az abszolút konvergenciát azért kell feltennünk, hogy az összeg ne függhessen az összeadandók sorrendjétől. Természetesen ha véges, akkor nincs gond a konvergenciával.
Ha folytonos eloszlású sűrűségfüggvénnyel (ekkor általában egy intervallum), akkor várható értéke legyen
feltéve, hogy az integrál abszolút konvergens (azaz, ha a kifejezésben -et -ra cseréljük, véges értéket kapunk).
Végül tegyük fel, hogy kevert eloszlású, azaz megadható hozzá egy parciális súlyfüggvény, ami a halmazon értelmezett, továbbá egy tartományon értelmezett parciális sűrűségfüggvény, ahol és diszjunktak, megszámlálható, általában egy intervallum, és . Ekkor várható értékét definiáljuk a következőképpen:
ahol megint csak feltesszük az összeg és az integrál abszolút konvergenciáját.
Az változó várható értékét nevezhetjük az eloszlása középértékének is, és jelölhetjük -vel. Mit is értünk az alatt, hogy várható értéke épp az eloszlásának középértéke? Gondoljunk az eloszlásra úgy, mint egy tömegeloszlásra (a teljes tömeg 1 egység). Ekkor a várható érték nem más, mint a fizikában jól ismert tömegközéppont. Az alábbi két képen diszkrét súly- és folytonos sűrűségfüggvények láthatók, mindkét esetben a -vel jelölt pont a tömegközéppont, vagy nevezhetnénk egyensúlyi pontnak is.
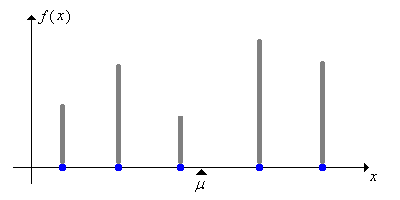
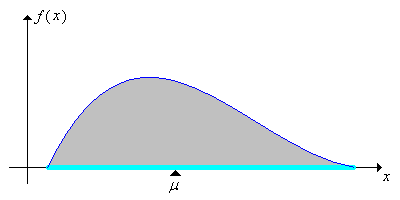
Emlékezzünk vissza, hogy már bevezettünk két fogalmat, melyek valamilyen értelemben az eloszlás közepét jellemezték:
A várható érték valószínűségszámítási szemléltetéséhez tekintsünk egy összetett kísérletet, ami nem más, mint az eredeti kísérletünk többszöri megismétlése. Így független valószínűségi változók egy , sorozatát kapjuk, ahol minden valószínűségi változó eloszlása megegyezik eloszlásával. Statisztikai kifejezéssel élve mintát veszünk eloszlásából. Az átlagos érték, vagy mintaátlag darab kísérlet után
Az átlagos érték konvergál az várható értékhez, amint . Ezt a konvergenciát matematikailag precíz értelemben a nagy számok törvénye fogalmazza meg, ami a valószínűségszámítás egyik legfontosabb tétele. A szimulációs feladatokban látni fogjuk majd, hogyan teljesül a nagy számok törvénye a gyakorlatban.
Legyen , és . Ekkor középpontú -edik momentuma a következő kifejezés:
A 0 középpontú momentumokat röviden csak momentumoknak mondjuk. Továbbá az középpontú momentumok a centrált momentumok. A második centrált momentum különösen fontos, részletes tárgyalása a szórásnégyzet fejezetben található. Bizonyos esetekben összes momentumának ismeretében meghatározhajuk eloszlását. Ezzel kapcsolatos részletek a generátorfüggvények fejezetben találhatóak.
Az valószínűségi változó várható értéke természetesen függ a kísérlethez tartozó valószínűségi mértéktől . Ez a mérték lehet egy feltételes valószínűségi mérték, valamely feltételre vonatkozólag. (Természetesen ). Erre szokásos jelölés . A feltételes várható érték szintén a fenti definíciók segítségével számolható, azzal a különbséggel, hogy az eredeti súly-, vagy sűrűségfüggvényt az feltételes súly-, vagy sűrűségfüggvényre kell cserélnünk. Vegyük észre, hogy (jelöléstől eltekintve) nem vezettünk be új fogalmat. Így minden, a várható értékre vonatkozó állítás megfelelője igaz feltételes várható értéke is.
Ebben a fejezetben a várható érték legfontosabb tulajdonságait vesszük sorra. Ahol ezt külön nem jelöljük, ott mindig feltesszük, hogy a várható érték létezik.
Egy valós értékű valószínűségi változó várható értéke az eloszlásának középértéke. Ez az intuitív kép sokkal hasznosabb, mint első ránézésre gondolnánk. Hiszen ha meghatározzuk valószínűségi változónk különböző függvényeinek várható értékét, az eloszlás sok érdekes tulajdonságára következtethetünk.
Legyen tehát egy értékű valószínűségi változó, és legyen egy -ből -be képező függvény. Ekkor valós értékű valószínűségi változó, tehát meghatározhatjuk -et. Ha azonban a definíció alapján szeretnénk ezt a várható értéket kiszámolni, ismernünk kellene az transzformált valószínűségi változó eloszlását, ami általában nehezen meghatározható. Szerencsére ennél sokkal egyszerűbb számolási módszert biztosít a változócserére vonatkozó tétel. Hívhatnánk ezt a tételt a figyelmetlen statisztikus törvényének is, hisz annyira egyszerű, hogy sokszor észre sem vesszük, hogy egy tételt alkalmazunk és nem a definíciót.
Lássuk be, hogy ha diszkrét eloszlású egy megszámlálható halmazon, továbbá a súlyfüggvénye , akkor
Hasonlóan, ha folytonos eloszlású az halmazon, sűrűségfüggvénye , akkor
A folytonos esetre vonatkozó állítást több lépésben fogjuk bizonyítani, mégpedig a 2. Feladat, 53. Feladat és 56. Feladat segítségével.
Bizonyítsuk be a változócserére vonatkozó tételt abban a speciális esetben, amikor -értékű folytonons valószínűségi változó, pedig diszkrét (azaz képtere megszámlálható).
Az alábbi feladatok a várható érték legfontosabb tulajdonságait tartalmazzák. Az állítások általában igazak, de a bizonyítás során érdemes külön kezelni a diszkrét és a folytonos esetet, és természetesen az előző tételt használni. A következőkben és valós értékű valószínűségi változók, valós konstans. Mindig feltesszük, hogy a feladatokban szereplő várható értékek léteznek.
Lássuk be, hogy .
Igazoljuk, hogy .
Tegyük fel, hogy a kísérletünktől függő valós értékű valószínűségi változók, pedig konstansok. Ekkor az előző két feladat következménye, hogy
Azaz, a várható érték lineáris. Ez egy roppant fontos tulajdonság, ezért érdemes intuitív szinten is érteni. Ehhez a várható érték értelmezésénél kimondott nagy számok törvényét hívjuk segítségül:
Tegyük fel, hogy valós értékű valószínűségi változók, közös várható értékkel. Ha még azt is feltesszük, hogy függetlenek és azonos eloszlásúak, akkor egy elemű véletlen mintánk van a közös eloszlásukból.
A következő feladatokban a várható értékre vonatkozó egyenlőtlenségeket bizonyíthatjuk be. Az első a legegyszerűbb, melyet érdemes a további feladatokban alkalmazni.
Tegyük fel, hogy . Lássuk be, hogy
Tegyük fel, hogy . Lássuk be, hogy:
Tehát azt kaptuk, hogy a várható érték monoton. A linearitás után talán ez a második legfontosabb tulajdonság.
Lássuk be, hogy
Igazoljuk a következőket:
Tegyük fel, hogy folytonos eloszlású értékű valószínűségi változó, melynek sűrűségfüggvénye -ra szimmetrikus, azaz , amint . Lássuk be, hogy ha létezik, akkor .
Legyenek és független valós értékű valószínűségi változók. Lássuk be, hogy .
Az előző feladat következménye, hogy a független valószínűségi változók korrelálatlanok. Ez egy nagyon fontos eredmény! Tegyük fel, hogy és független , illetve értékű valószínűségi változók, továbbá -en és -n értelmezett valós értékű függvények. Ekkor és független valós értékű valószínűségi változók, így
Egy konstansra úgy is gondolhatunk, mint egy valószínűségi változóra, amely 1 valószínűséggel a értéket veszi fel. Eloszlását gyakran a pontra koncentrált eloszlásnak nevezik. Lássuk be, hogy .
Legyen egy indikátor valószínűségi változó (azaz olyan változó, amely csak a 0 és 1 értékeket veszi fel). Lássuk be, hogy .
Azaz ha az esemény indikátora, akkor . Tehát bizonyos értelemeben a várható érték általánosítja a valószínűség fogalmát. Peter Whittle Probability via Expectation című könyvében az alapfogalom a valószínűség helyett a várható érték.
Tegyük fel, hogy diszkrét egyenletes eloszlású az véges halmazon.
Legyen folytonos egyenletes eloszlású az intervallumon.
Legyen egyenletes eloszlású az intervallumon és integrálható függvény -ből -be. Igazoljuk, hogy a függvény intervallumon vett átlaga a szokásos értelemben.
Tegyük fel, hogy egyenletes eloszlású a intervallumon.
Egy hagyományos kocka alatt hat oldalú dobókockát értünk. Az igazságos kocka olyan, hogy ha feldobjuk, mindegyik oldalára azonos valószínűséggel esik. Az egy-hat irányban lapos kocka egy hagyományos kocka, ami feldobás után az 1 és 6 értékeket , a 2, 3, 4 és 5 értékeket valószínűséggel mutatja.
Két hagyományos igazságos kockát feldobtunk, a kapott értékeket az párba lejegyeztük. Határozzuk meg a következő valószínűségi változók várható értékét:
A kockadobálós kísérletben válasszunk két szabályos kockát. Figyeljük meg a valószínűségi súlyfüggvény alakját és a dobások összegének, minimumának és maximumának várható értékét. Szimuláljunk 1000 kísérletet, és figyeljük meg, hogyan konvergálnak a mintaátlagok az elméleti várható értékhez mindhárom esetben.
Oldjuk meg a 20. Feladatot egy-hat irányban lapos kocka esetén!
A Bernoulli kísérletek folyamata nem más, mint egy független, azonos eloszlású indikátor változókból álló vektor. Megbízhatóság-elméleti kifejezéssel élve jelöli az -edik kísérlet eredményét, ahol 1 jelenti a sikert, 0 a kudarcot. A siker valószínűsége a folyamat paramétere. Ezt a folyamatot James Bernoulli-ről nevezték el. A Bernoulli kísérletek című külön fejezetben találhatunk további részleteket.
Az első kísérletből a sikeresek száma . Ez a valószínűségi változó binomiális eloszlású és paraméterekkel, és a súlyfüggvénye:
Igazoljuk, hogy kétféleképpen is:
A binomiális eloszlás kísérletében változtassuk -et és -t, és vizsgáljuk meg a súlyfüggvény alakját, valamint a várható értéket. Néhány és értékre szimuláljunk 1000 kísérletet, és figyeljük meg, hogyan konvergál a mintaátlag a várható értékhez.
Jelölje az első sikeres kísérlet sorszámát. Ez is egy valószínűségi változó, amely geometriai eloszlású paraméterrel, és a súlyfüggvénye:
Igazoljuk, hogy .
A negatív binomiális kísérletben válasszunk -et, így visszakapjuk a geometriai eloszlást. Változtassuk -t, és figyeljük meg a súlyfüggvény alakját és a várható értéket. Néhány értékre szimuláljunk 1000 kísérletet, és figyeljük meg, hogyan konvergál a mintaátlag a várható értékhez.
Tegyük fel, hogy egy populáció egyedből áll, ezek közül darab 1-es típusú, darab pedig 0-ás típusú. Visszatevés nélkül kiválasztunk véletlen egyedet. Legyen az -edik kiválasztott egyed típusa. Ekkor tudjuk, hogy azonos eloszlású valószínűségi változók, melyek azonban nem függetlenek. Valójában ez a valószínűségi változó sorozat felcserélhető.
Legyen az 1-es típusú kiválasztott egyedek száma, azaz . Ekkor hipergeometriai eloszlású az alábbi súlyfüggvénnyel:
Igazoljuk, hogy kétféleképpen is:
A golyók és urnák kísérletben, változtassuk , és értékét, majd figyeljük meg a súlyfüggvény alakját és a várható értéket. Néhány és értékre szimuláljunk 1000 kísérletet, és figyeljük meg, hogyan konvergál a mintaátlag a várható értékhez.
A Poisson eloszlás súlyfüggvénye
ahol
paraméter (nevét Simeon Poisson-ról kapta). Gyakran használják egy adott halmazba eső véletlen pontok
számának leírására, ekkor nyilván az
paraméter arányos a halmaz méretével. A Poisson eloszlás részletes tárgyalása a Poisson folyamat fejezetben található.
Tegyük fel, hogy Poisson eloszlású paraméterrel. Igazoljuk, hogy , azaz a Poisson eloszlás paramétere egyben a várható értéke is.
A Poisson kísérletben a paraméter . Változtassuk a paramétert, majd figyeljük meg a súlyfüggvény alakját és a várható értéket. Néhány konkrét paraméterválasztás mellett szimuláljunk 1000 kísérletet, és figyeljük meg, hogyan konvergál a mintaátlag a várható értékhez.
Az exponenciális eloszlás egy folytonos eloszlás, melynek sűrűségfüggvénye:
ahol
egy paraméter, melyet gyakran rátának neveznek. Ez az eloszlás jól modellezi bizonyos gépek, alkatrészek meghibásodásáig eltelt időt, vagy egyes érkezési időpontokat
. Például ilyen eloszlásúak a Poisson folyamat felújtás hosszai. Az exponenciális eloszlás részletes tárgyalása a Poisson folyamat fejezetben található.
Tegyük fel, hogy exponenciális eloszlású rátával.
A valószínűségi változók kísérletében válasszuk ki a gamma eloszlást. Állítsuk be a értéket, így exponenciális eloszlást kapunk. Változtassuk az paraméter értékét, és figyeljük meg, hogyan változik a várható érték. Ezután paraméterválasztással szimuláljunk 1000 kísérletet, és figyeljük meg, hogyan konvergál a mintaátlag a várható értékhez.
A gamma eloszlás egy folytonos eloszlás, melynek sűrűségfüggvénye:
ahol
-et gyakran az eloszlás rendjének,
-et pedig a rátájának nevezik. Jól modellezi bizonyos érkezési idők
eloszlását. A gamma eloszlás részletes tárgyalása a Poisson folyamat fejezetben található. Ha
független, azonos eloszlású
paraméterű exponenciális eloszlású valószínűségi változók, akkor
-edrendű,
rátájú gamma eloszlású valószínűségi változó.
Tegyük fel, hogy gamma eloszlású és pereméterekkel. Igazoljuk, hogy kétféleképpen is:
A valószínűségi változók kísérletében válasszuk ki a gamma eloszlást. Változtassuk a paraméterértékeket, és vizsgáljuk meg a várható érték és a sűrűségfüggvény viszonyát. Néhány paraméterrel szimuláljunk 1000 kísérletet, és figyeljük meg, hogyan konvergál a mintaátlag a várható értékhez.
A következő eloszlások a béta eloszlások családjába tartoznak, melyek alkalmazhatók például véletlenszerűen kialakuló arányok modellezésére. A béta eloszlás részletes tárgyalása a Nevezetes eloszlások fejezetben található.
Tegyük fel, hogy sűrűségfüggvénye .
A valószínűségi változók kísérletében válasszuk ki a béta eloszlást, és állítsuk be az , paraméterértékeket (így kapjuk vissza az előző feladat eloszlását). Szimuláljunk 1000 kísérletet, és figyeljük meg, hogyan konvergál a mintaátlag a várható értékhez.
Tegyük fel, hogy egy gömb véletlen sugara az valószínűségi változó, melynek sűrűségfüggvénye . Határozzuk meg a következő valószínűségi változók várható értékét:
Tegyük fel, hogy sűrűségfüggvénye . Ezt a speciális béta eloszlást arcus szinusz eloszlásnak is nevezik.
A Pareto eloszlás egy folytonos valószínűségi eloszlás, melynek sűrűségfüggvénye:
ahol paraméter. Az eloszlás Vilfredo Pareto-ról kapta a nevét. Ez egy lassan lecsengő eloszlás, melyet gyakran alkalmaznak különböző pénzügyi mennyiségek (pl. bevétel) modellezésére. A Pareto eloszlást részletesen a Nevezetes eloszlások fejezetben tárgyaljuk.
Tegyük fel, hogy Pareto eloszlású paraméterrel. Igazoljuk, hogy
A valószínűségi változók kísérletében válasszuk ki a Pareto eloszlást. A következő paraméterértékekre szimuláljunk 1000 kísérletet. Figyeljük meg az empirikus várható érték viselkedését.
A Cauchy eloszlás sűrűségfüggvénye:
Nevét Augustin Cauchy-ról kapta. Ez az eloszlás tagja a Student eloszláscsaládnak. A eloszlásokról részletesen a Nevezetes eloszlások fejezetben olvashatunk.
Tegyük fel, hogy Cauchy eloszlású.
A valószínűségi változók kísérletében válasszuk ki a Student féle eloszlást. Állítsuk be az paraméterértéket, így megkapjuk a Cauchy eloszlást. Szimuláljunk 1000 kísérletet és figyeljük meg az empirikus várható érték viselkedését.
A standard normális eloszlás egy folytonos eloszlás, melynek sűrűségfüggvénye: . A Normális eloszlás rendkívül széles körben alkalmazható, például hibával terhelt mérési eredmények modellezésére. Részletes tárgyalása a Nevezetes eloszlások fejezetben található.
Tegyük fel, hogy standard normális eloszlású.
Legyen ismét standard normális eloszlású, és , . Ekkor normális eloszlású hely- és skála-paraméterekkel . Igazoljuk, hogy , azaz a hely-paraméter épp a várható érték.
A valószínűségi változók kísérletében válasszuk ki a normális eloszlást. Változtassuk a paramétereket, és figyeljük meg, hogyan változik a várható érték. Néhány paraméter esetén szimuláljunk 1000 kísérletet, és figyeljük meg, hogyan konvergál az empirikus várható érték a valódi várható értékhez.
Tegyük fel, hogy az valószínűségi változó pár együttes sűrűségfüggvénye . Határozzuk meg a következő várható értékeket:
5 vadász áll lesben, amikor elrepül előttük 10 kacsa. Mindegyik vadász véletlenszerűen kiválaszt egy kacsát és lelövi (a vadászok jól céloznak, mindannyian eltalálják a kiválasztott kacsát). Határozzuk meg a lelőtt kacsák számának várható értékét! Segítség: a lelőtt kacsák számát írjuk fel indikátor valószínűségi változók összegeként.
A kacsák-vadászok problémakör részletes vizsgálata a Különböző mintaelemek száma részben található a Véges mintavételezési modellek fejezetben.
Igazoljuk a Markov egyenlőtlenséget (nevét Andrei Markov-ról kapta): Ha nemnegatív valószínűségi változó, akkor tetszőleges esetén
Legyen diszkrét, vagy folytonos eloszlású nemnegatív valószínűségi változó. Igazoljuk, hogy
Segítség: A fenti képletben szereplő tagot fejezzük ki az változó súly-, vagy sűrűségfüggvényével (diszkrét esetben egy összeget, folytonos esetben egy integrált kapunk). Ezután cseréljük fel a két integrálás (illetve az integrálás és az összegzés) sorrendjét.
Az 52. feladat eredményét használva igazoljuk a változócserére vonatkozó tételt arra az esetre, amikor folytonos eloszlású az halmazon, sűrűségfüggvénye , és egy nemnegatív, -en értelmezett függvény.
A következő eredmény hasonló az 52. feladatban bizonyítotthoz, azonban csak nemnegatív egész értékű valószínűségi változókra vonatkozik:
Tegyük fel, hogy egy -értékű diszkrét valószínűségi változó. Igazoljuk, hogy
Segítség: az első egyenlőséghez írjuk fel a valószínűséget összeg alakban súlyfüggvényének segítségével, majd cseréljük fel a két összegzést. A második egyenlőség egy változócserével adódik.
Az 52. feladat segítségével egységesen definiálható a várható érték a diszkrét, folytonos és vegyes eloszlások esetére. Sőt, igazából a sűrűségfüggvény létezését sem kell feltennünk. Tekintsük az 52. feladat formuláját az valószínűségi változó várható értékét definiáló kifejezésnek abban az esetben, ha nemnegatív. Ezután -nek definiáljuk a pozitív és negatív részét a következő képletekkel:
Igazoljuk, hogy
Legyen valós értékű valószínűségi változó. Ekkor és (azaz pozitív és negatív részei) nemnegatív valószínűségi változók. Így, feltéve, hogy vagy , definiálhatjuk a várható értéket a következő módon:
Ezzel a definícióval a korábbi definíciót, mint tételt be lehet bizonyítani. Lényegében ez az 52. feladat megoldása lenne, azzal a különbséggel, hogy a feladatban a feltétel és az állítás szerepét felcserélnénk.
Most már bebizonyíthatjuk a változócserére vonatkozó tételt, ha folytonos eloszlású az halmazon sűrűségfüggvénnyel, valamint egy -en értelmezett valós értékű függvény. Segítség: bontsuk fel -et pozitív és negatív részre, majd alkalmazzuk az 53. feladat eredményét.
A következő néhány feladatban egy fontos összefüggést, a Jensen egyenlőtlenséget bizonyítjuk (nevét Johan Jensen-ről kapta). Szükségünk lesz a következő definícióra. Egy valós értékű függvényt, mely egy intervallumon van értelmezve, -en konvexnek nevezünk, ha minden esetén találhatók és számok (melyek természetesen függhetnek -től), hogy
A egyenest a pontbeli támaszegyenesnek nevezzük. Tehát egy konvex függvénynek az értelmezési tartomány minden pontjában van legalább egy támaszegyenese.
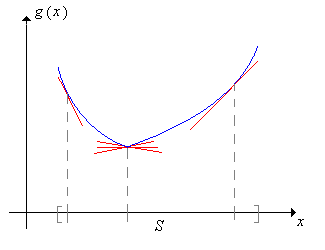
Egy közismert tétel az analízisből: ha kétszer folytonosan differenciálható, és a második deriváltja -en nemnegatív, akkor konvex az halmazon. (Hiszen a pontbeli érintő támaszegyenes is egyben -ben minden -re.)
Igazoljuk a Jensen egyenlőtlenséget: Legyen egy értékű valószínűségi változó ( egy intervallum). Legyen továbbá az -en konvex függvény. Ekkor
Segítség: A konvexitás definíciójában válasszunk -et, és cseréljük -et -re. Ezután vegyünk várható értéket.
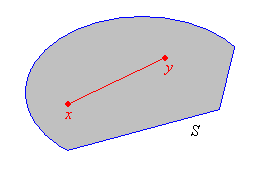
Nézzük meg, hogyan általánosítható a Jensen egyenlőtlenség magas dimenziós esetekre. A két dimenziós változata különösen fontos, hiszen ebből fogunk néhány egyenlőtlenséget levezetni a következő fejezetben. Egy halmazt konvexnek nevezünk, ha minden -beli pontpárra az őket összekötő szakasz is -ben van:
Egy -en értelmezett valós értékű függvényt konvexnek nevezünk, ha minden esetén található és (amik természetesen függhetnek -től), hogy
esetén gráfját a pontbeli támaszsíknak nevezzük. Analízisbeli tétel, hogy ha kétszer folytonosan differenciálható, és a második derivált mátrixa pozitív szemidefinit -en, akkor konvex.
Tegyük fel, hogy az függvény értékkészlete az halmaz. Legyen . Igazoljuk a Jensen egyenlőtlenséget: ha konvex és valós értékű, konvex függvény -en, akkor
Segítség: A konvexitás definíciójában legyen és . Vegyünk várható értéket az egyenlőtlenség mindkét oldalán. A véletlen vektorok és mátrixok várható értékét részletesen a következő fejezetben tárgyaljuk.
Mind az egy, mind az -dimenziós esetben tekinthetünk konkáv függvényt. Ekkor a definícióban és a Jensen egyenlőtlenségben is megfordul a relációs jel.
Tegyük fel, hogy sűrűségfüggvénye ahol , azaz exponenciális eloszlású rátával.
Tegyük fel, hogy súlyfüggvénye ahol , azaz geometriai eloszlású, és a siker valószínűsége . Ez a valószínűségi változó egy Bernoulli kísérletsorozatban az első sikeres kísérlet sorszámát adja meg.
Tegyük fel, hogy sűrűségfüggvénye , ahol azaz Pareto eloszlású paraméterrel.
Tegyük fel, hogy sűrűségfüggvénye
Legyen pozitív számok halmaza. Igazoljuk, hogy a számtani közép nem kisebb a geometriai középnél:
Segítség: Legyen egyenletes eloszlású az halmazon, és alkalmazzuk a Jensen egyenlőtlenséget a függvényre.