The (American) roulette wheel has 38 slots numbered 00, 0, and 1-36. As shown in the picture below,
Except for 0 and 00, the slots on the wheel alternate between red and black. The strange order of the numbers on the wheel is intended so that high and low numbers, as well as odd and even numbers, tend to alternate.
According to Richard Epstein, roulette is the oldest casino game still in operation. It's invention has been variously attributed to Blaise Pascal, the Italian mathematician Don Pasquale, and several others. In any event, the roulette wheel was first introduced into Paris in 1765.
The roulette experiment is very simple. The wheel is spun and then a small ball is rolled in a groove, in the opposite direction as the motion of the wheel.. Eventually the ball falls into one of the slots. Naturally, we assume mathematically that the wheel is fair, so that the random variable that gives the slot number of the ball is uniformly distributed over the sample space
Thus, for each
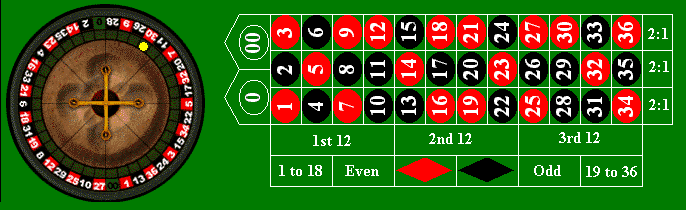
As with craps, roulette is a popular casino game because of the rich variety of bets that can be made. The picture above shows the roulette table and indicates some of the bets we will study. All bets turn out to have the same expected value (negative, of course).
A straight bet is a bet on a single number, and pays .
Let denote the winnings on a unit straight bet. Show that
In the roulette experiment, select the single number bet. Run the simulation 1000 times, updating every 10 runs and watch the apparent convergence of the empirical density and moments of to the true density and moments. Suppose that you bet $1 on each of the 1000 games. What would your net winnings be?
A 2-number bet (or a split bet) is a bet on two adjacent numbers in the roulette table. The bet pays if either of the chosen numbers comes up and loses otherwise.
Let denote the winnings on a unit split bet. Show that
In the roulette experiment, select the 2 number bet. Run the simulation 1000 times, updating every 10 runs and watch the apparent convergence of the empirical density and moments of to the true density and moments. Suppose that you bet $1 on each of the 1000 games. What would your net winnings be?
A 3-number bet (or row bet) is a bet on the three numbers in a vertical row. The bet pays if one of the three numbers comes up and loses otherwise.
Let denote the winnings on a unit row bet. Show that
In the roulette experiment, select the 3-number bet. Run the simulation 1000 times, updating every 10 runs and watch the apparent convergence of the empirical density and moments of to the true density and moments. Suppose that you bet $1 on each of the 1000 games. What would your net winnings be?
A 4-number bet or a square betis a bet on the four numbers that form a square on the roulette board. The bet pays if one of the 4 numbers comes up and loses otherwise.
Let denote the winnings on a unit 4-number bet. Show that
In the roulette experiment, select the 4-number bet. Run the simulation 1000 times, updating every 10 runs and watch the apparent convergence of the empirical density and moments of to the true density and moments. Suppose that you bet $1 on each of the 1000 games. What would your net winnings be?
A 6-number bet or 2-row bet is a bet on the 6 numbers in two adjacent rows. The bet pays if one of the chosen numbers comes up and loses otherwise.
Let denote the winnings on a unit 6-number bet. Show that
In the roulette experiment, select the 6-number bet. Run the simulation 1000 times, updating every 10 runs and watch the apparent convergence of the empirical density and moments of to the true density and moments. Suppose that you bet $1 on each of the 1000 games. What would your net winnings be?
A 12-number bet is a bet on 12 numbers. In particular, a column bet is bet on any one of the three columns of 12 numbers running horizontally along the table. Other 12-number bets are the first 12 (1-12), the middle 12 (13-24), and the last 12 (25-36). A 12-number bet pays if one of the chosen numbers comes up and loses otherwise. In particular, a 12-number bet loses if 0 or 00 comes up.
Let denote the winnings on a unit 12-number bet. Show that
In the roulette experiment, select the 12-number bet. Run the simulation 1000 times, updating every 10 runs and watch the apparent convergence of the empirical density and moments of to the true density and moments. Suppose that you bet $1 on each of the 1000 games. What would your net winnings be?
An 18-number bet is a bet on 18 numbers. In particular, A color bet is a bet either on red or on black. A parity bet is a bet on the odd numbers from 1 to 36 or the even numbers from 1 to 36. The low bet is a bet on the numbers 1-18, and the high bet is the bet on the numbers from 19-36. An 18-number bet pays if one of the chosen numbers comes up and loses otherwise. In particular, an 18-number bet loses if 0 or 00 comes up.
Let denote the winnings on a unit 18-number bet. Show that
In the roulette experiment, select the 18-number bet. Run the simulation 1000 times, updating every 10 runs and watch the apparent convergence of the empirical density and moments of to the true density and moments. Suppose that you bet $1 on each of the 1000 games. What would your net winnings be?
Although all bets in roulette have the same expected value, the standard deviations vary inversely with the number of numbers selected. What are the implications of this for the gambler?