Recall that with the strategy of timid play in red and black, the gambler makes a small constant bet, say $1, on each game until she stops. Thus, on each game, the gambler's fortune either increases by 1 or decreases by 1, until the fortune reaches either 0 or the target (which we assume is a positive integer). Thus, the fortune process is a random walk on the fortune space with 0 and as absorbing barriers.
As usual, we are interested in the probability of winning and the expected number of games. The key idea in the analysis is that after each game, the fortune process simply starts over again, but with a different initial value. This is an example of the Markov property, named for Andrei Markov. A separate chapter on Markov Chains explores these random processes in more detail. In particular, this chapter has sections on Birth-Death Chains and Random Walks on Graphs, particular classes of Markov chains that generalize the random processes that we are studying here.

Our analysis based on the Markov property suggests that we treat the initial fortune as a variable. Thus, we will denote the probability that the gambler reaches the target , starting with an initial fortune by
By conditioning on the outcome of the first game, show that satisfies
The difference equation is linear (in the unknown function ), homogeneous (because each term involves the unknown function ), and second order (because 2 is the difference between the largest and smallest fortunes in the equation).
Show that the characteristic equation of the difference equation in Exercise 1 is , and that the roots are and .
Show that if , then the roots are distinct. Show that, in this case, the probability that the gambler reaches her target is
Show that if , the characteristic equation has a single root 1 that has multiplicity 2. Show that, in this case, the probability that the gambler reaches her target is simply the ratio of the initial fortune to the target fortune:
Thus, we have the distribution of the final fortune in all cases:
In the red and black experiment, choose Timid Play. Vary the initial fortune, target fortune, and game win probability and note how the probability of winning the game changes. For various values of the parameters, run the experiment 1000 times with an update frequency of 10 and note the apparent convergence of the relative frequency of winning a game to the probability of winning a game.
Show that as a function of , for fixed and ,
Show that is continuous as a function of , for fixed and Specifically, use L'Hospital's Rule to show that the expression in Exercise 3 converges to the expression in Exercise 4, as .
Show that for fixed and , increases from 0 to 1 as increases from 0 to 1.
The picture below show the typical shape of the graph of for , , and ,
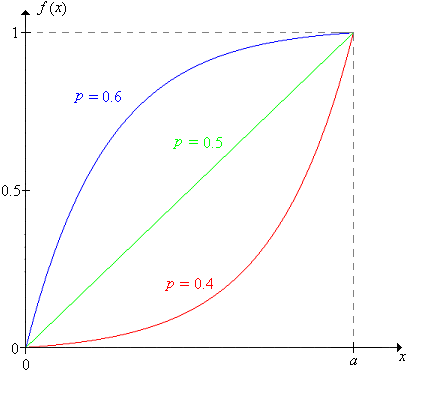
Now let us consider the expected number of games needed with timid play, when the initial fortune is :
By conditioning on the outcome of the first game, show that satisfies
The difference equation in the last exercise is linear, second order, but non-homogeneous (because of the constant term 1 on the right side). The corresponding homogeneous equation is the equation satisfied by the win probability function . Thus, only a little additional work is needed here.
Show that if , then
where is the win probability function given in Exercise 3
Show that if , then
Consider as a function of the initial fortune , for fixed values of the game win probability and the target fortune .
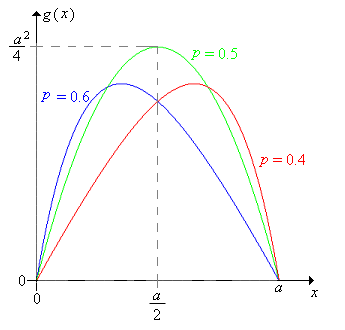
Show that is continuous as a function of , for fixed and Specifically, show that the expression in Exercise 10 converges to the expression in Exercise 11, as .
For many parameter settings, the expected number of games is surprisingly large. For example, suppose that and the target fortune is 100. If the gambler's initial fortune is 1, then the expected number of games is 99, even though half of the time, the gambler will be ruined on the first game. If the initial fortune is 50, the expected number of games is 2500.
In the red and black experiment, select Timid Play. Vary the initial fortune, the target fortune and the game win probability and notice how the expected number of games changes. For various values of the parameters, run the experiment 1000 times with an update frequency of 100. Note the apparent convergence of the sample mean number of games to the expect value.
What happens if the gambler makes constant bets, but with an amount higher than 1? The answer to this question may give insight into what will happen with bold play.
In the red and black game, set the target fortune to 16, the initial fortune to 8, and the win probability to 0.45. Play 10 games with each of the following strategies. Which seems to work best?
We will need to embellish our notation to indicate the dependence on the target fortune. Let
Now fix and suppose that the target fortune is and the initial fortune is . If the gambler plays timidly (betting $1 each time), then of course, her probability of reaching the target is . On the other hand:
Suppose that the gambler bets $2 on each game. Argue that the fortune process corresponds to timid play with initial fortune and target fortune and that therefore the probability that the gambler reaches the target is .
Thus, we need to compare the probabilities and .
Show that for and hence
Thus, it appears that increasing the bets is a good idea if the games are unfair, a bad idea if the games are favorable, and makes no difference if the games are fair.
What about the expected number of games played? It seems almost obvious that if the bets are increased, the expected number of games played should decrease, but a direct analysis using Exercise 10 is harder than one might hope (try it!), We will use a different method, one that actually gives better results. Specifically, we will have the $1 and $2 gamblers bet on the same underlying sequence of games, so that the two fortune processes are defined on the same sample space. Then we can compare the actual random variables (the number of games played), which in turn leads to a comparison of their expected values. Recall that this general method is referred to as coupling.
Let denote the fortune after games for the gamble making $1 bets (simple timid play). Argue that is the fortune after games for the gambler making $2 bets (with the same initial fortune, betting on the same sequence of games). Assume again that the initial fortune is and the target fortune where . Let denotes the number of games played by the $1 gambler, and denotes the number of games played by the $2 gambler, Argue that
Of course, the expected values agree (and are both 0) if or . Exercise 18 shows that is stochastically smaller than when the gamblers are not playing the same sequence of games (so that the random variables are not defined on the same sample space).
Generalize the analysis in this subsection to compare timid play with the strategy of betting $ on each game (let the initial fortune be and the target fortune .
It appears that with unfair games, the larger the bets the better, at least in terms of the probability of reaching the target. Thus, we are naturally led to consider bold play.