Tegyük fel, hogy egy elemű véletlen minta a normális eloszlásból várható értékkel és szórással. Általában mindkét paraméter ismeretlen, így a paramétertér .
Ebben az alfejezetben -re és -ra vonatkozó próbákat fogunk konstruálni, amik a hipotézisvizsgálat legfontosabb esetei közé tartoznak. Különböző próbafüggvényeken alapuló próbákat fogunk kifejleszteni. Ezen próbák némelyike jobban teljesít, mint mások, attól függően, mely paraméterek ismertek. Ezen alfejezet párhuzamos az Intervallumbecslés fejezet Becslés a normál modellben alfejezetével, és speciálisan a dualitás a halmazbecslés és a hipotézisvizsgálat között fontos szerepet fog játszani.
Végső soron a próbafüggvényeink mindegyike létrehozható az alap próbafüggvényekből, amik az adatváltozóink standardizált
változatai.
és
esetén legyen:
Mutassuk meg, hogy egy elemű véletlen minta normális eloszlásból várható értékkel és szórással!
Speciálisan egy véletlen minta a standard normális eloszlásból. Így elfogadhatónak tűnik, hogy a alapján létrehozott próbafüggvények hasznosak lehetnek -ra illetve -re - mint illetve előzetes értékeire - vonatkozó próbákhoz.
Idézzük fel, hogy az adatvektorunk mintaátlaga
Az első próbafüggvényünk a mintaátlag lineáris transzformációja. és esetén legyen:
Mutassuk meg, hogy normális eloszlású várható értékkel és szórással!
Speciálisan a valószínűségi változó az standardizáltja és standard normális eloszlású; ez a változó volt az egyik pivot változó, amit a konfidencia halmazok a normál modellben konstruálásához használtunk.
Mutassuk meg, hogy a 2. feladatban szereplő próbafüggvény felírható az 1. feladatban szereplő alap próbafüggvények segítségével a következőképpen:
Szokás szerint jelölje a standard normális sűrűségfüggvényt és a standard normális eloszlásfüggvényt. esetén jelölje a standard normális eloszlás -ed rendű kvantilisét. Azaz . kiválasztott értékeire megkapható a Student-féle eloszlás táblázat utolsó sorából, a standard normális eloszlás táblázatából, a kvantilis appletből vagy a legtöbb statisztikai szoftvercsomagból.
Mutassuk meg vagy idézzük fel a következő tulajdonságokat! A (d) rész az analízis inverzfüggvény tételéből következik (inverz függvény deriválása).
Mutassuk meg, hogy tetszőleges és esetén a következő próba szignifikancia szintje ! Elutasítjuk versus -t akkor és csak akkor, ha . Ekvivalensen: elfogadjuk -t akkor és csak akkor, ha
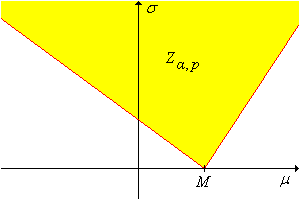
Jegyezzük meg, hogy az 5. feladatban szereplő próba a Becslés a normál modellben alfejezetben, a pivot változóval konstruált konfidencia halmaz duálisa. Azaz a -ok halmaza, amire elfogadjuk -t szinten, pontosan megegyezik a -ra vonatkozó szintű konfidencia halmazzal. Ez a halmaz látható a fenti ábrán. Megjegyezzük, hogy az szignifikancia szint aránya a pivot változó eloszlásának jobb farkában; az aránya a bal farokban. Az egyenlő-farkú eset, amikor , a legáltalánosabban használt; ezt a próbát hívjuk torzítatlannak.
Világos, hogy egy két valós paraméterre vonatkozó próba, ami egy valós értékű próbafüggvényen alapul, nem lehet nagyon jó. Az alfejezet hátralévő részében feltesszük, hogy ismert. Ez gyakran, bár nem mindig, mesterséges feltételezés; lásd a 43. feladatot, ami példa arra, hogy ez a feltételezés elfogadható lehet. Ha ismert, az alap próbafüggvényünket a következőképpen írjuk fel: .
Mutassuk meg, hogy tetszőleges és esetén a következő próba szignifikancia szintje :
Az (a) részben a torzítatlan próba - - a leggyakrabban használt: Elutasítjuk versus -t akkor és csak akkor, ha vagy
A 6. feladatban szereplő próbák esetén mutassuk meg, hogy elfogadjuk -t szignifikancia szinten akkor és csak akkor, ha beleesik a megfelelő szintű konfidencia intervallumba!
Idézzük fel, hogy egy paraméterre vonatkozó próba erőfüggvénye a nullhipotézis elutasításának valószínűsége a paraméter valódi értékének a függvényében. A következő feladatok a 6. feladatban szereplő próbák erőfüggvényét vizsgálják.
Mutassuk meg, hogy a 6(a) feladatban szereplő próba erőfüggvényét a következő képlet adja meg, és kielégíti az alábbi tulajdonságokat:
Mutassuk meg, hogy a 6(b) feladatban szereplő próba erőfüggvényét a következő képlet adja meg, és kielégíti az alábbi tulajdonságokat:
Mutassuk meg, hogy a 6(c) feladatban szereplő próba erőfüggvényét a következő képlet adja meg, és kielégíti az alábbi tulajdonságokat:
Mutassuk meg, hogy a 6. feladatban szereplő három próba mindegyike az mintanagyság növelésével vagy a szórás csökkentésével egyenletesen erősebb próbát eredményez!
Az átlag próba kísérletben válasszuk a normál próbafüggvényt és válasszunk normális mintaeloszlást szórással, szignifikancia szintet, mintanagyságot és -t! Futtassuk a kísérletet ezerszer, tízes frissítési gyakorisággal az eloszlás valódi várható értékének néhány értékére! minden értékére figyeljük meg a nullhipotézis elutasításának relatív gyakoriságát! Vázoljuk fel a tapasztalati erőfüggvényt!
Az átlag becslés kísérletben válasszuk a normál pivot változót és válasszunk normális eloszlást várható értékkel és szórással, konfidencia szintet és mintanagyságot! Mindhárom konfidencia intervallum típusra futtassuk a kísérletet hússzor, minden futás után frissítve! Állítsuk fel a megfelelő hipotéziseket, és adjuk meg a szignifikancia szintet, és minden futás esetén adjuk meg a -ra vonatkozó halmazt, amire a nullhipotézist el kellene utasítani!
Sok esetben az első lépés a kísérlet megtervezése úgy, hogy a szignifikancia szint legyen, és úgy, hogy adott alternatíva esetén a próba ereje egy adott legyen.
A 6. feladatban szereplő bármelyik egyoldali próba esetén mutassuk meg, hogy szignifikancia szintű és alternatívára vonatkozó erejű próbához szükséges mintanagyság a következő:
Útmutatás: Legyen az erőfüggvény egyenlő -val, és oldjuk meg -re az egyenletet!
A torzítatlan, kétoldali próba esetén mutassuk meg, hogy szignifikancia szintű és alternatívára vonatkozó erejű próbához szükséges közelítő mintanagyság a következő:
Útmutatás: A 8. feladatban szereplő, a kétoldali próbára vonatkozó erőfüggvény esetén hanyagoljuk el az első tagot, ha és hanyagoljuk el a második tagot, ha .
Ebben a részben a korrigált tapasztalati szórásnégyzethez kapcsolódó próbafüggvényeket fogunk használni. Először is idézzük fel, hogy a korrigált tapasztalati szórásnégyzet:
Továbbá idézzük fel, hogy az egyik legfontosabb speciális tulajdonsága a normál mintáknak az, hogy az mintaátlag és az korrigált tapasztalati szórásnégyzet függetlenek. és esetén definiáljuk a következőket:
Idézzük fel, hogy -t már használtuk, mint a tapasztalati szórásnégyzet speciális esetét, abban a valószínűtlen esetben, ha a várható érték ismert volt.
Mutassuk meg, hogy az 1. feladatban szereplő alap próbafüggvények négyzetösszege:
Mutassuk meg, hogy , ahol a 2. feladatban szereplő próbafüggvény! Így speciálisan ebből következik, hogy szintén felírható az 1. feladatban szereplő alap próbafüggvények segítségével.
Mutassuk meg, hogy
A 18. feladatban szereplő változók voltak a pivot változók, amiket a konfidencia halmazok a normál modellben megkonstruálásához használtunk.
Jelölje illetve a szabadságfokú khi-négyzet eloszlás sűrűség- illetve eloszlásfüggvényét. Továbbá esetén jelölje az eloszlás -ed rendű kvantilisét; definíció szerint . és kiválasztott értékeire megkapható a khi-négyzet eloszlás táblázatból, a kvantilis appletből vagy a legtöbb statisztikai programcsomagból.
Mutassuk meg vagy idézzük fel a következő tulajdonságokat! A (c) rész az analízis inverzfüggvény tételéből következik:
Mutassuk meg, hogy tetszőleges és esetén a következő próba szignifikancia szintje : Elutasítjuk versus -t akkor és csak akkor, ha vagy . Ekvivalensen mutassuk meg, hogy elfogadjuk -t akkor és csak akkor, ha
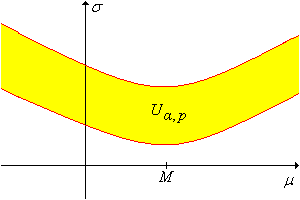
Jegyezzük meg, hogy a 20. feladatban szereplő próba a Becslés a normál modellben alfejezetben, a pivot változóval konstruált konfidencia halmaz duálisa. Azaz a -ok halmaza, amire elfogadjuk -t szinten, pontosan megegyezik az szintű konfidencia halmazzal -ra. Ez a halmaz látható a fenti ábrán.
Mutassuk meg, hogy tetszőleges és esetén a következő próba szignifikancia szintje : Elutasítjuk versus -t akkor és csak akkor, ha vagy . Ekvivalensen mutassuk meg, hogy elfogadjuk -t akkor és csak akkor, ha
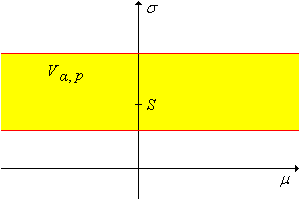
Jegyezzük meg, hogy a 21. feladatban szereplő próba a Becslés a normál modellben alfejezetben, a pivot változóval konstruált konfidencia halmaz duálisa. Azaz a -ok halmaza, amire elfogadjuk -t szinten, pontosan megegyezik az szintű konfidencia halmazzal -ra. Ez a halmaz látható a fenti ábrán.
Megjegyezzük, hogy mindkét próba esetén az szignifikancia szint aránya a pivot változó eloszlásának jobb farkában; az aránya a bal farokban. Az egyenlő-farkú eset, amikor , a legáltalánosabban használt; ezt a próbát hívjuk torzítatlannak.
Világos, hogy egy két valós paraméterre vonatkozó próba, ami egy valós értékű próbafüggvényen alapul, nem lehet nagyon jó. Viszont mivel a próbafüggvény nem ad semmilyen információt -ről, természetes, hogy ezt csak -ra vonatkozó próbák esetén használjuk. Ha ismert lenne, használhatnánk az próbafüggvényt is. Ezen rész minden eredménye érvényes lenne helyett -gyel. Viszont az, hogy a ismert, nagyon mesterséges feltételezés.
Mutassuk meg, hogy tetszőleges és esetén a következő próba szignifikancia szintje :
Az (a) részben a torzítatlan próba - - a leggyakrabban használt: Elutasítjuk versus -t akkor és csak akkor, ha vagy
A 22. feladatban szereplő próbák esetén mutassuk meg, hogy elfogadjuk -t szignifikancia szinten akkor és csak akkor, ha beleesik a megfelelő szintű konfidencia intervallumba!
Idézzük fel, hogy egy paraméterre vonatkozó próba erőfüggvénye a nullhipotézis elutasításának valószínűsége a paraméter valódi értékének a függvényében. A következő feladatok a 22. feladatban szereplő próbák erőfüggvényeit vizsgálják.
Mutassuk meg, hogy a 22(a) feladatban szereplő próba erőfüggvényét a következő képlet adja meg, és kielégíti az alábbi tulajdonságokat:
Mutassuk meg, hogy a 22(b) feladatban szereplő próba erőfüggvényét a következő képlet adja meg, és kielégíti az alábbi tulajdonságokat:
Mutassuk meg, hogy a 22(c) feladatban szereplő próba erőfüggvényét a következő képlet adja meg, és kielégíti az alábbi tulajdonságokat:
Mutassuk meg, hogy a 22. feladatban szereplő három próba mindegyike az mintanagyság növelésével egyenletesen erősebb próbát eredményez!
A szórásnégyzet próba kísérletben válasszuk a normális eloszlást 0 várható értékkel, és válasszunk 0,1 szignifikancia szintet, 10-es mintanagyságot, és 1,0 teszt szórást! A valódi szórás különböző értékeire futtassuk a kísérletet ezerszer, tízes frisítési gyakorisággal! Jegyezzük fel a nullhipotézis elutasításának relatív gyakoriságát, és ábrázoljuk az empirikus erő görbét!
A szórásnégyzet becslés kísérletben válasszuk a normális eloszlást 0 várható értékkel és 2 szórással, és válasszunk 0,90 konfidencia szintet és 10-es mintanagyságot! Futtassuk a kísérletet hússzor, minden futás után frissítve! Állítsuk fel a megfelelő hipotéziseket, és adjuk meg a szignifikancia szintet, és minden futásra adjuk meg a teszt szórások halmazát, amire a nullhipotézist el kellene utasítani!
Következő próbafüggvényünk jó próbáihoz vezet anélkül a feltételezés nélkül, hogy ismert. -re definiáljuk:
Mutassuk meg, hogy tetszőleges és esetén:
Speciálisan ebből következik, hogy felírható az 1. feladatban szereplő alap próbafüggvények segítségével.
Mutassuk meg vagy idézzük fel, hogy Student-féle eloszlású szabadságfokkal!
Ez a változó volt az egyik pivot változó, amit felhasználtunk a Becslés a normál modellben alfejezetben. Amikor , eloszlása mint nem-centrális eloszlás ismert.
Szokás szerint esetén illetve jelöli a szabadságfokú eloszlás sűrűség- illetve eloszlásfüggvényét. Továbbá esetén jelölje ezen eloszlás -ed rendű kvantilisét; azaz . és kiválasztott értékeire megkapható a Student-féle eloszlás táblázatból vagy a kvantilis appletből.
Mutassuk meg vagy idézzük fel a következő tulajdonságokat! A (d) rész az analízis inverzfüggvény tételéből következik.
Mutassuk meg, hogy tetszőleges és esetén a következő próba szignifikancia szintje : Elutasítjuk versus -t akkor és csak akkor, ha . Ekvivalensen, elfogadjuk -t akkor és csak akkor, ha
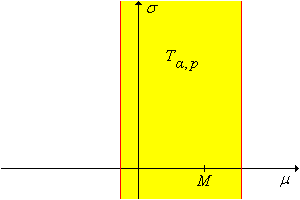
Jegyezzük meg, hogy a 33. feladatban szereplő próba a Becslés a normál modellben alfejezetben, a pivot változóval konstruált konfidencia halmaz duálisa. Azaz a -ok halmaza, amire elfogadjuk -t szinten, pontosan megegyezik a -ra vonatkozó szintű konfidencia halmazzal. Ez a halmaz látható a fenti ábrán. Megjegyezzük, hogy az szignifikancia szint aránya a pivot változó eloszlásának jobb farkában; az aránya a bal farokban. Az egyenlő-farkú eset, amikor , a legáltalánosabban használt; ezt a próbát hívjuk torzítatlannak.
Mivel a próbafüggvény nem ad semmilyen információt -ról, nincs értelme ezt a paramétert a hipotézisbe bevonni.
Mutassuk meg, hogy tetszőleges és esetén a következő próba szignifikancia szintje :
Az (a) részben a torzítatlan próba - - a leggyakrabban használt:
Elutasítjuk versus -t akkor és csak akkor, ha vagy
A 34. feladatban szereplő próbák esetén mutassuk meg, hogy elfogadjuk -t szignifikancia szinten akkor és csak akkor, ha beleesik a megfelelő szintű konfidencia intervallumba!
Ezen próbák -értéke kiszámítható az szabadságfokú -eloszlás eloszlásfüggvényének segítségével.
Mutassuk meg, hogy a 34. feladatban szereplő próbák -értéke rendre:
Az átlag próba kísérletben válasszuk a Student próbafüggvényt, és válasszunk normális mintaeloszlást szórással, szignifikancia szintet, mintanagyságot és -t! Futtassuk a kísérletet ezerszer, tízes frissítési gyakorisággal az eloszlás valódi várható értékének néhány értékére! minden értékére figyeljük meg a nullhipotézis elutasításának relatív gyakoriságát! Vázoljuk fel a tapasztalati erőfüggvényt!
Az átlag becslés kísérletben válasszuk a student pivot változót, és válasszunk normális mintaeloszlást 0 várható értékkel és 2 szórással! Legyen a konfidencia szint 0,90 és a mintanagyság 10 ! Mindhárom konfidencia intervallum típusra futtassuk a kísérletet hússzor, minden futás után frissítve! Állítsuk fel a megfelelő hipotéziseket és adjuk meg a szignifikancia szintet, és minden futás esetén adjuk meg a -ra vonatkozó halmazt, amire a nullhipotézist el kellene utasítani!
A 34. feladatban szereplő próbák erőfüggvénye explicit kiszámítható a nem-centrális eloszlásfüggvény segítségével. Az erőfüggvények grafikonjának alakja hasonló ahhoz az esethez, mikor ismert, és ahogy a 8. feladatban, a 9. feladatban és a 10. feladatban szerepelt.
Ha ismert egy felső korlát a szórásra, akkor adott konfidencia szinthez és hibahatárhoz szükséges mintanagyságra vonatkozó konzervatív becslés megkapható a 14. feladat és a 15. feladat módszerével.
Az alapfeltevésünk az volt, hogy a megalapozó minta eloszlása normális. Természetesen valós statisztikai problémák esetén valószínűtlen, hogy sokat tudunk a minta eloszlásáról, még arról sem, hogy vajon normális-e. Tegyük fel, hogy a tényleges megalapozó eloszlás nem normális. Amikor az elég nagy, a mintaátlag eloszlása közelítően normális lesz a centrális határeloszlás tétel szerint, és így a átlagra vonatkozó próbák még közelítően érvényesek lehetnek. Másrészt a szórásnégyzetre vonatkozó próbák kevésbé robusztusak, ha eltérünk a normalitástól. A következő feladatok ezeket a gondolatokat fejtik ki.
Az átlag próba kísérletben válasszuk a gamma eloszlást 1 alakparaméterrel és 1 skálaparaméterrel! A három különböző próba valamint különböző szignifikancia szintek, mintanagyságok és értékek esetén futtassuk a kísérletet ezerszer, tízes frissítési gyakorisággal! Minden konfiguráció esetén jegyezzük fel elutasításának relatív gyakoriságát! Amikor igaz, hasonlítsuk össze a relatív gyakoriságot a szignifikancia szinttel!
Az átlag próba kísérletben válasszuk a intervallumon egyenletes eloszlást! A három különböző próba valamint különböző szignifikancia szintek, mintanagyságok és értékek esetén futtassuk a kísérletet ezerszer, tízes frissítési gyakorisággal! Minden konfiguráció esetén jegyezzük fel elutasításának relatív gyakoriságát! Amikor igaz, hasonlítsuk össze a relatív gyakoriságot a szignifikancia szinttel!
Hogy milyen nagynak kell lenni az mintanagyságnak, hogy a próbák jól működjenek, természetesen a megalapozó eloszlástól függ; minél inkább eltér ez az eloszlás a normálistól, annál nagyobb szükséges. Szerencsére a normálishoz tartó konvergencia gyors a centrális határeloszlás tétel szerint, és így, ahogy a gyakorlatban megfigyelhettük, viszonylag kis mintanagysággal (30 vagy több) is célt érhettünk a legtöbb esetben.
A szórásnégyzet próba kísérletben válasszuk a gamma eloszlást 1 alakparaméterrel és 1 skálaparaméterrel! A három különböző próba valamint különböző szignifikancia szintek, mintanagyságok és értékek esetén futtassuk a kísérletet ezerszer, tízes frissítési gyakorisággal! Minden konfiguráció esetén jegyezzük fel elutasításának relatív gyakoriságát! Amikor igaz, hasonlítsuk össze a relatív gyakoriságot a szignifikancia szinttel!
A szórásnégyzet próba kísérletben válasszuk a intervallumon egyenletes eloszlást! A három különböző próba valamint különböző szignifikancia szintek, mintanagyságok és értékek esetén futtassuk a kísérletet ezerszer, tízes frissítési gyakorisággal! Minden konfiguráció esetén jegyezzük fel elutasításának relatív gyakoriságát! Amikor igaz, hasonlítsuk össze a relatív gyakoriságot a szignifikancia szinttel!
Egy bizonyos gépalkatrész hossza 10 centiméter elméletileg. Valójában a gyártási folyamat tökéletlensége miatt a tényleges hossz valószínűségi változó. A szórás a folyamat sajátosságai miatt nem változik az idők során. Történeti adatokból tudjuk, hogy a szórás nagy pontossággal 0,3. Másrészt az átlag különböző gyártási paraméterek módosításával befolyásolható, és így elég gyakran változhat valamilyen ismeretlen értékre. A következő próbát végeznénk el: versus .
Egy bizonyos cég burgonya csipszének tömege a hirdetés szerint 250 gramm. Valójában a tömeg (grammban) valószínűségi változó. Tegyük fel, hogy egy 75 elemű mintára az átlag 248 és a szórás 5. Végezzük el a következő próbákat 0,05 szignifikancia szinten:
Egy telemarketing cégnél a telefonos kérelem hossza (másodpercekben) valószínűségi változó. Egy 50 hívásból álló mintára az átlag 310 és a szórás 25. Következtethetünk-e 0,1 szignifikancia szinten arra, hogy
Egy bizonyos farmon az őszibarack tömege szüret idején (unciában) valószínűségi változó. Egy százelemű minta esetén az átlag 8,2 és a szórás 1,0. Következtethetünk-e 0,01 szignifikancia szinten arra, hogy
Egy bizonyos típusú építési munkán az órabér valószínűségi változó 1,25 szórással. Egy 25 dolgozóból álló minta alapján az átlagbér 6,75 dollár volt. Következtethetünk-e 0,01 szignifikancia szinten arra, hogy ?
A Michelson adatok esetén teszteljük le, hogy a fénysebesség nagyobb-e, mint 730 (+299000) km/sec 0,005 szignifikancia szinten!
A Cavendish adatok esetén teszteljük le, hogy a Föld sűrűsége kevesebb-e, mint 5,5-szerese a víz sűrűségének 0,05 szignifikancia szinten!
A Short adatok esetén teszteljük le, hogy a Nap parallaxisa különbözik-e 9 szögmásodperctől 0,1 szignifikancia szinten!
A Fisher írisz adatok esetén hajtsuk végre a következő próbákat 0,1 szinten!