]> Becslés a kétmintás normál modellben
  1. Virtual Laboratories
  2. 7. Intervallumbecslés
  3. 1
  4. 2
  5. 3
  6. 4
  7. 5

4. Becslés a kétmintás normál modellben

Ebben az alfejezetben a kétmintás normál modellben és a kétváltozós normál modellben fellépő becslési problémákat fogjuk vizsgálni. Ez az alfejezet megfelel a Hipotézisvizsgálat a kétmintás normál modellben alfejezetnek a Hipotézisvizsgálat fejezetben.

A kétmintás normál modell

Tegyük fel, hogy X X 1 X 2 X m egy m elemű véletlen minta a μ várható értékű és σ szórású normális eloszlásból, és hogy Y Y 1 Y 2 Y n egy n elemű véletlen minta a ν várható értékű és τ szórású normális eloszlásból. Továbbá tegyük fel, hogy az X és az Y minták függetlenek. Rendszerint a paraméterek ismeretlenek, így a μ ν σ τ paramétervektorunk paramétertere: 2 0 2

Ez a szituáció gyakran fellép, amikor a valószínűségi változók a populáció objektumainak minket érdeklő mérőszámait reprezentálják, és a mintákat két különböző eljárásnak vetettük alá. Például páciensek egy csoportjának a vérnyomása érdekel minket. Az X vektor a kontrolcsoport vérnyomásadatait tartalmazza, míg az Y vektor azok vérnyomásadatait tartalmazza, akik egy új gyógyszert kapnak. Hasonlóan, a kukorica hozama érdekel minket. Az X vektor tartalmazza a hozam adatokat, ahol minta az egyik féle műtrágyát kapta, míg az Y vektor egy más műtrágyát kapott minta adatait tartalmazza.

Rendszerint a két minta eloszlásparamétereinek (várható érték, szórás) összehasonlítása a célunk. Ebben az alfejezetben konfidencia halmazokat fogunk konstruálni a paramétervektorra, amik a szórások hányadosára illetve a várható értékek különbségére vonatkozó konfidencia intervallumokhoz fognak vezetni. Ahogy a megelőző becslési problémáknál, a konstrukció a megfelelő pivot változóktól függ.

Egy általános U U 1 U 2 U k minta esetén, ami egy a várható értékű eloszlásból származik, a szokásos jelöléseinket fogjuk használni a mintaközépre és a tapasztalati szórásnégyzetre. Emlékezzünk vissza ezen statisztikák speciális tulajdonságaira, ha a mintavételezett eloszlás normális.

M U 1 k i 1 k U i ,  W 2 U a 1 k i 1 k U i a 2 ,  S 2 U 1 k 1 i 1 k U i M U 2

F pivot változón alapuló konfidencia halmazok

Mutassuk meg, hogy a következő valószínűségi változó F eloszlású m szabadságfokkal a számlálóban és n szabadságfokkal a nevezőben! Mutassuk meg, hogy a változó egy pivot változó μ ν σ τ -ra és μ ν τ σ -ra!

W 2 X μ τ 2 W 2 Y ν σ 2

Most p 0 1 , m 0 és n 0 esetén jelölje f m n p az F eloszlás p -ed rendű kvantilisét, ahol m a szabadságfok a számlálóban és n a szabadságfok a nevezőben. m , n és p kiválasztott értékeire f m n p kiszámítható a kvantilis applet vagy a legtöbb statisztikai és matematikai szoftvercsomag segítségével.

Használjuk az 1. feladatban szereplő pivot változót, hogy megmutassuk, hogy tetszőleges α 0 1 és p 0 1 esetén 1 α szintű konfidencia halmaz μ ν σ τ -ra:

μ ν σ τ f m n α p α W 2 Y ν W 2 X μ τ 2 σ 2 f m n 1 p α W 2 Y ν W 2 X μ

Nem túl sok betekintést kaphatunk ezen konfidencia halmaz mint a négydimenziós paramétertér részhalmaza struktúrájába. A halmaz természetesen nem korlátos, mivel négy paramétert becslünk egy pivot változóval. Ha μ és ν ismertek (ismerjük be, ez mesterséges feltételezés), a halmaz 1 α szintű konfidencia halmaz lesz σ τ -ra. Ez a halmaz szintén nem korlátos, az általános alakja a lenti ábrán látható:

Confidence set

Megjegyezzük, hogy ha μ és ν ismertek, a konfidencia halmaz egy korlátos konfidencia intervallumot ad τ 2 σ 2 -re, és négyzetgyököt vonva, egy korlátos konfidencia intervallumot ad τ σ -ra. Ahogy mindig, a p szám határozza meg a pivot változó eloszlása jobb-farkának arányát α -hoz viszonyítva (ahogy 1 p a bal-farok arányát). Szokás szerint, a legfontosabb speciális esetek a következők:

Más F pivot változón alapuló konfidencia halmazok

Ez a rész megfelel az előzőnek, azzal a különbséggel, hogy a korrigált tapasztalati szórásnégyzetet használjuk a speciális változata helyett.

Mutassuk meg, hogy a következő valószínűségi változó F eloszlású m 1 szabadságfokkal a számlálóban és n 1 szabadságfokkal a nevezőben! Mutassuk meg, hogy a változó pivot változó μ ν σ τ -ra, σ τ -ra és τ σ -ra:

S 2 X τ 2 S 2 Y σ 2

Használjuk a 3. feladatban szereplő pivot változót, hogy megmutassuk, hogy α 0 1 és p 0 1 esetén 1 α szintű konfidencia halmaz μ ν σ τ -ra:

μ ν σ τ f m 1 n 1 α p α S 2 Y S 2 X τ 2 σ 2 f m 1 n 1 1 p α S 2 Y S 2 X

Ez a konfidencia halmaz a konstrukcióból adódóan nem ad semmilyen információt μ -ről és ν -ről. Mint egy σ τ -ra vonatkozó konfidencia halmaz, az alakja hasonló az előzőhöz:

Confidence set

Továbbá a konfidencia halmazunk korlátos konfidencia intervallumot ad τ 2 σ 2 -re, és négyzetgyököt vonva, korlátos konfidencia intervallumot ad τ σ -ra. Ahogy mindig, a p szám határozza meg a pivot változó eloszlása jobb-farkának arányát α -hoz viszonyítva (ahogy 1 p a bal-farok arányát α -hoz). Szokás szerint, a legfontosabb speciális esetek:

Normál pivot változón alapuló konfidencia halmazok

A következőkben egy olyan pivot változót tanulmányozunk, amely konfidencia halmazai jobbak a várható értékek különbségét tekintve.

Mutassuk meg, hogy M Y M X normál eloszlású ν μ várható értékkel és σ 2 m τ 2 n szórásnégyzettel!

Mutassuk meg, hogy a következő valószínűségi változó standard normális eloszlású! Mutassuk meg, hogy a változó pivot változó μ ν σ τ -ra és ν μ σ τ -ra:

M Y M X ν μ> σ 2 m τ 2 n

Szokás szerint, p 0 1 esetén z p -vel jelöljük a standard normális eloszlás p -ed rendű kvantilisét. Idézzük fel, hogy z p z 1 p

Használjuk a 6. feladatban szereplő pivot változót, hogy megmutassuk, hogy tetszőleges α 0 1 és p 0 1 esetén 1 α szintű konfidencia halmaz μ ν σ τ -ra:

μ ν σ τ M Y M X z 1 α p σ 2 m τ 2 n ν μ M Y M X z α α p σ 2 m τ 2 n

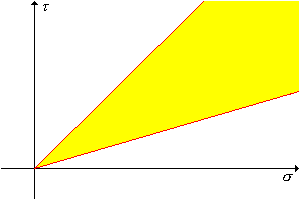
Újfent nem túl sok betekintést kaphatunk ezen konfidencia halmaz - mint a négydimenziós paramétertér részhalmaza - struktúrájába. A halmaz természetesen nem korlátos, mivel négy paramétert becslünk egy pivot változóval. Ha σ és τ ismertek, akkor a halmaz 1 α szintű konfidencia halmaz μ ν -re. Ez a halmaz szintén nem korlátos, de könnyű megérteni; a határoló görbék 1 meredekségű egyenesek. A halmaz általános alakja a lenti ábrán látható. Jegyezzük meg, hogy a konfidencia sáv szélessége determinisztikus.

Confidence set

Továbbá, ha σ és τ ismertek, a konfidencia halmaz korlátos konfidencia intervallumokat ad a várható értékek különbségére, ν μ -re, és gyakran ez az érdeklődésre számot tartó paraméterünk. Az a feltételezés, hogy σ és τ ismertek, rendszerint mesterséges, de kevésbé, mint az első részbeli feltevésünk, hogy μ és ν ismertek.

Ahogy mindig, a p szám határozza meg a pivot változó eloszlása jobb-farkának α -hoz viszonyított arányát (ahogy 1 p a bal-farok arányát α -hoz). Szokás szerint, a legfontosabb speciális esetek:

Student-féle t pivot változón alapuló konfidencia halmazok

Az utolsó konstrukciónk olyan pivot változó létrehozására irányul, ami hasznos a várható értékek különbségének, ν μ -nek, a becsléséhez, anélkül, hogy a σ és τ szórásokat ismernünk kellene. Viszont ennek ára van, fel kell tételeznünk, hogy a szórások megegyeznek, σ τ , de a közös érték ismeretlen. Ez a feltételezés elfogadható, ha a mért változó olyan belső változékonysággal rendelkezik, ami nem módosul akkor sem, ha különböző eljárásoknak vetjük alá a populáció objektumait.

Mutassuk meg, hogy a 6.feladatban szereplő pivot változó a következő lesz:

M Y M X ν μ σ 1 m 1 n

Hogy megkonstruáljuk a pivot változót, először is szükségünk lesz σ 2 pontbecslésére. Természetes megközelítés, ha az S 2 X és S 2 Y korrigált tapasztalati szórásnégyzetek szabadságfokaikkal súlyozott átlagát vesszük (ezt σ 2 összesített becslésének hívjuk). Így legyen

S 2 X Y m 1 S 2 X n 1 S 2 Y m n 2

Mutassuk meg, hogy a következő változó khi-négyzet eloszlású m n 2 szabadságfokkal! Útmutatás: Fejezzük ki a változót, mint független khi-négyzet változók összegét!

m 1 S 2 X n 1 S 2 Y σ 2

Mutassuk meg, hogy M Y M X és S 2 X Y függetlenek! Útmutatás: Mutassuk meg vagy idézzük fel a következő változópárok függetlenségét:

  1. M X S X és M Y S Y
  2. M X és S X
  3. M Y és S Y

Mutassuk meg, hogy a következő valószínűségi változó t -eloszlású m n 2 szabadságfokkal! Mutassuk meg, hogy a változó pivot változó μ ν σ τ -ra, μ ν -re és ν μ -re:

M Y M X ν μ S X Y 1 m 1 n

Útmutatás: Mutassuk meg, hogy a valószínűségi változó felírható, mint Z V m n 2 , ahol Z a 8. feladatban szereplő valószínűségi változó és V a 9. feladatban szereplő valószínűségi változó, továbbá Z és V függetlenek a 10. feladat szerint.

k 0 és p 0 1 esetén jelölje t k p a k szabadságfokú t -eloszlás p -ed rendű kvantilisét. k és p kiválasztott értékeire t k p értékeit megtaláljuk a Student-féle t -eloszlás tábázatban, megkaphatjuk a kvantilis appletből vagy a legtöbb statisztikai szoftvercsomagból. Szimmetria miatt t k p t k 1 p

Használjuk a 11. feladatban szereplő pivot változót, hogy megmutassuk, hogy tetszőleges α 0 1 és p 0 1 esetén 1 α szintű konfidencia halmaz μ ν σ τ -ra:

μ ν σ τ M Y M X t m n 2 1 α p S X Y 1 m 1 n ν μ M Y M X t m n 2 α α p S X Y 1 m 1 n

A konfidencia halmaz konstrukciójából adódóan nem ad semmilyen információt σ -ról és τ -ról. Mivel egy 1 α szintű konfidencia halmaz μ ν -re, a halmaz alakja megfelel az előző részben szereplő általános alaknak, kivéve, hogy a sáv szélessége véletlen.

Confidence set

Végül természetesen a konfidencia halmaz korlátos konfidencia intervallumot ad a várható értékek különbségére, ν μ -re, és sokszor ez a minket érdeklő paraméter.

Ahogy mindig, a p szám határozza meg a pivot változó eloszlása jobb-farkának arányát α -hoz viszonyítva (ahogy 1 p a bal-farok arányát α -hoz). A legfontosabb speciális esetek:

Becslés a kétváltozós normál modellben

Ebben a részben egy olyan modellt vizsgálunk, ami látszólag hasonlít a kétmintás normál modellhez, de sokkal egyszerűbb. Tegyük fel, hogy

X 1 Y 1 X 2 Y 2 X n Y n

egy n elemű valószínűségi minta az X Y kétváltozós normális eloszlásból X μ , Y ν , X σ 2 , Y τ 2 , és X Y δ jellemzőkkel.

Így mintapár helyett páros minta áll rendelkezésünkre. Ez a típusú modell gyakran fellép előtte és utána kísérletekben, ahol egy populáció n objektumáról gyűjtünk adatokat egy eljárás előtt és után. Például n páciens vérnyomás adatait jegyezzük fel egy bizonyos gyógyszer használata előtt és után. Ahogy a kétmintás normál modell esetén, a cél rendszerint itt is a várható értékek különbségének becslése.

A szokásos jelöléseket fogjuk használni X X 1 X 2 X n és Y Y 1 Y 2 Y n mintaközepére és szórásnégyzetére. Emlékezzünk vissza, az X Y minta kovarianciája

S X Y 1 n 1 i 1 n X i M X Y i M Y

Mutassuk meg, hogy Y X Y 1 X 1 Y 2 X 2 Y n X n egy n elemű véletlen minta Y X eloszlásából, ami normális eloszlású a következő paraméterekkel:

  1. Y X ν μ
  2. Y X σ 2 τ 2 2 δ

Mutassuk meg, hogy

  1. M Y X M Y M X
  2. S 2 Y X S 2 X S 2 Y 2 S X Y

Az Y X különbségekből vett minta beleillik az egyváltozós normál modellbe. A Becslés a normál modellben alfejezetben leírtak alkalmazhatók a ν μ σ 2 τ 2 2 δ paraméterekre vonatkozó konfidencia halmazok és intervallumok képzésére.

Tegyük fel, hogy X X 1 X 2 X n és Y Y 1 Y 2 Y n független minták normális eloszlásból. Ezek az adatok mindkét modellhez illeszkednek - a kétmintás normál modellhez és a kétváltozós normál modellhez is. Melyik eljárás működik jobban a várható értékek különbségének ( ν μ ) becslésére,

  1. ha a σ és τ szórások ismertek?
  2. ha a σ és τ szórások ismeretlenek?

Számítási feladatok

Egy új orvosságot fejlesztenek a vér bizonyos vegyi anyagának csökkentésére. Páciensek egy 36 fős mintája placebot kap, míg egy 49 fős minta a gyógyszert kapja. Jelölje X a placebot kapó páciensek adatait és Y a gyógyszert kapó páciensek adatait (mg-ban). A statisztikák a következők: m X 87 , s X 4 , m Y 63 , s Y 6 .

  1. Számítsuk ki a 90%-os konfidencia intervallumot τ σ -ra!
  2. Feltételezve, hogy σ τ , számítsuk ki a 90%-os konfidencia intervallumot ν μ -re!
  3. Az (a)-t figyelembe véve, elhihető-e a σ τ feltételezés?
  4. (b)-t figyelembe véve, hatásos-e a gyógyszer?

Egy cég azt állítja, hogy egy bizonyos növényi táplálékkiegészítő növeli az intelligenciát. Egy 25 főből álló minta standard IQ-tesztet végzett a kiegészítő használata előtt és után. Jelölje X a kísérlet előtti IQ-t és Y a kísérlet utáni IQ-t. A használat előtti és utáni statisztikák m X 105 , s X 13 , m Y 110 , s Y 17 , s X Y 190 . Hihető-e a cég állítása?

A Fisher írisz adatok esetén jelölje X a Versicolor írisz sziromhosszát és Y a Virginica írisz sziromhosszát.

  1. Számítsuk ki a 90%-os konfidencia intervallumot τ σ -ra!
  2. Feltételezve, hogy σ τ , számítsuk ki a 90%-os konfidencia intervallumot ν μ -re!
  3. Az (a)-t figyelembe véve, elhihető-e a σ τ feltételezés?

Egy üzem két gépe körkeresztmetszetű rudakat gyárt, melyek átmérője (cm-ben) kritikus. Jelölje X az első gép által gyártott rudak átmérőjét és Y a második gép által gyártott rudak átmérőjét. Az első gépről való 100 elemű mintára az átlag 10,3 és a szórás 1,2. A második gépről való 100 elemű mintára az átlag 9,8 és a szórás 1,6.

  1. Számítsuk ki a 90%-os konfidencia intervallumot τ σ -ra!
  2. Feltételezve, hogy σ τ , számítsuk ki a 90%-os konfidencia intervallumot ν μ -re!
  3. Elfogadható-e (a) alapján a σ τ feltételezés?

  1. Virtual Laboratories
  2. 7. Intervallumbecslés
  3. 1
  4. 2
  5. 3
  6. 4
  7. 5