]> Becslés a normál modellben
  1. Virtual Laboratories
  2. 7. Intervallumbecslés
  3. 1
  4. 2
  5. 3
  6. 4
  7. 5

2. Becslés a normál modellben

Bevezetés

A normál modell

Tegyük fel, hogy X X 1 X 2 X n egy véletlen minta a normális eloszlásból, μ átlaggal és σ 0 szórással. Ebben a fejezetben konfidencia halmazokat fogunk készíteni μ -re és σ -ra. Ezek a halmazbecslések legfontosabb speciális esetei közé tartoznak. Egy kapcsolódó alfejezet a témáról a Hipotézisvizsgálat a normál modellben, ami a Hipotézisvizsgálat fejezetben található.

Az alap pivot változó

Szokás szerint, a konfidencia halmaz konstruálását megfelelő pivot változó megkeresésével kezdjük. Első lépésként standardizáljuk az eredményváltozónkat, hogy egy alap pivot vektort képezzünk, amelyből a többi pivot változót elkészíthetjük. Így minden i esetén legyen

Z i X i μ σ

Mutassuk meg, hogy Z Z 1 Z 2 Z n egy n elemű véletlen minta a standard normális eloszlásból, és így egy pivot vektor μ σ -ra!

Normál pivot változón alapuló konfidencia halmazok

A pivot változó

Emlékezzünk vissza, hogy az X adatvektorunk mintaátlaga:

M 1 n i 1 n X i

Mutassuk meg, hogy M normális eloszlású μ átlaggal és σ 2 n szórásnégyzettel! Így a megfelelő standardizált változó standard normális eloszlású és pivot változó μ σ -ra:

Z M μ σ n

Mutassuk meg, hogy a 2. feladatban szereplő pivot változó felírható az 1. feladatban szereplő alap pivot változók segítségével a következőképpen:

Z 1 n i 1 n Z i

Szokás szerint jelöljük φ -vel a standard normális sűrűségfüggvényt és Φ -vel a standard normális eloszlásfüggvényt. p 0 1 esetén jelölje z p a standard normális eloszlás p -ed rendű kvantilisét. Azaz z p Φ p . p kiválasztott értékeire z p -t megkaphatjuk a t -eloszlás táblázatának utolsó sorából, a standard normális eloszlás táblázatából, a kvantilis appletből vagy a legtöbb statisztikai programcsomagból.

Lássuk be a következő tulajdonságokat! Használjuk az analízis inverz függvény tételét a (d) részhez:

  1. z 1 p z p
  2. z p , ha p 0
  3. z p , ha p 1
  4. z p 1 φ z p

Konfidencia halmazok

Használjuk a 2. feladatban szereplő pivot változót, hogy megmutassuk, tetszőleges p 0 1 és tetszőleges α 0 1 esetén 1 α szintű konfidencia halmaz μ σ -ra:

Z α p μ σ M z 1 p α σ n μ M z α p α σ n >

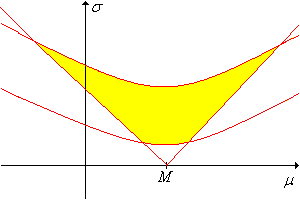
Mutassuk meg, hogy az 5. feladatban szereplő konfidencia halmaz egy kúp a μ σ paramétertérben M 0 csúccsal és n z 1 p α , n z α p α meredekségű határoló egyenesekkel, ahogy a lenti ábrán látható! (Megjegyezzük, hogy mindkét meredekség lehet negatív, vagy mindkettő pozitív.)

Confidence set based on a normal pivot variable

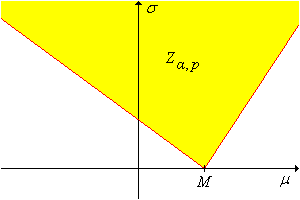
Megjegyezzük, hogy a tény, hogy a konfidencia halmaz nem korlátos, nem meglepő, mivel egy valós értékű pivot változót használtunk két valós paraméter becslésére. Viszont, ha σ ismert, a konfidencia halmaz egy korlátos konfidencia intervallum lesz μ -re. Geometriailag a konfidencia intervallum ebben az esetben az ismert σ magasságban húzott vízszintes egyenesből a konfidencia kúp által kimetszett szakasz lesz. Az a feltételezés, hogy σ ismert, rendszerint (de nem mindig) mesterséges. A 35. feladat példát ad olyan feltételekre, amelyek mellett a feltételezés elfogadható lehet. Elméletben kaphatunk konfidencia halmazt σ -ra, feltéve, hogy μ ismert; ezek a halmazok az ismert μ értéknél húzott függőleges egyenesből a konfidencia kúp által kimetszett szakaszok/félegyenesek lesznek. Viszont az a feltételezés, hogy μ ismert, majdnem mindig megalapozatlan, továbbá a σ -ra vonatkozó konfidencia halmazok általában nem lennének korlátosak.

Tanulmányozzuk a konfidencia kúp nagyságát! Az egyik módszer, hogy megvizsgáljuk a σ -nál lévő keresztszakasz L hosszát. Természetesen, ha σ ismert, akkor L egyszerűen a konfidencia intervallum hossza μ -re.

Mutassuk meg, hogy L z 1 p α z α p α σ n . Jegyezzük meg, hogy L determinisztikus! Mutassuk meg, hogy

  1. L α csökkenő függvénye rögzített n , p és σ esetén!
  2. L 0 , ha α 1 és L , ha α 0 rögzített n , p és σ esetén!
  3. L n csökkenő függvénye rögzített α , p és σ esetén!
  4. L 0 , ha n rögzített α , p és σ esetén!
  5. L σ növekvő függvénye rögzített α , p és n esetén!
  6. L 0 , ha σ 0 és L , ha σ rögzített α , p és n esetén!
  7. L szimmetrikus p 12 -re rögzített n , α és σ esetén!
  8. L csökken, ha p növekszik 0-tól 12 -ig és L növekszik, ha p növekszik 12 -től 1-ig rögzített n , α és σ esetén!
  9. L minimális, amikor p 12 rögzített n , α és σ esetén!
  10. L , ha p 0 , és ha p 1 rögzített n , α és σ esetén!

A 7. feladat ismét azt mutatja, hogy kompromisszum van a konfidencia szint és a konfidencia halmaz mérete közt. Ha n és p rögzített, akkor csökkenthetjük L -et, és így javíthatjuk a becslésünket, de csak a becslés konfidencia szintjének csökkentése árán. Fordítva, növelhetjük a becslésünk konfidencia szintjét, de csak a halmaz méretének növelése árán. p -t tekintve, az 1 α szintű kétoldali konfidencia halmazok közül a legjobb (és a mindig használt) az egyenlő-farkú halmaz:

Z α 1 2 μ σ M z 1 α 2 σ n μ M z 1 α 2 σ n

Ha σ ismert, akkor ez a halmaz az egyenlő-farkú konfidencia intervallumot adja μ -re. Figyeljük meg, hogy ez az intervallum szimmetrikus az M mintaátlagra!

Vizsgáljuk az 5. feladatot először a p 1 , majd a p 0 feltétel mellett! Mutassuk meg, hogy a következők 1 α szintű konfidencia halmazok μ σ -ra:

  1. Z α 1 μ σ M z 1 α σ n μ
  2. Z α 0 μ σ μ M z 1 α σ n

Ha σ ismert, az (a) rész 1 α szintű alsó konfidencia korlátot ad μ -re, és a (b) rész 1 α szintű felső konfidencia korlátot ad μ -re.

Használjuk az átlag becslés kísérletet az eljárás megismerésére! Válasszunk normál eloszlást és normál pivotot! Használjunk különböző paraméterértékeket, konfidencia szintet, mintanagyságot és intervallumtípust! Minden beállítás esetén futtassuk ezerszer a kísérletet, tízes frissítési gyakorisággal! Ahogy fut a szimuláció, figyeljük meg, hogy a konfidencia intervallum akkor és csak akkor tartalmazza az átlagot, ha a pivot változó értéke a kvantilesek közt van! Figyeljük meg a konfidencia intervallumok méretét és elhelyezkedését, valamint hogy a sikeres intervallumok aránya hogyan közelíti az elméleti konfidencia szintet!

A kísérlet megtervezése

Tegyük fel most, hogy σ ismert. Jelölje d a távolságot az M mintaátlag és valamelyik konfidencia határ közt. Azaz

d z α σ n

ahol z α z 1 α 2 a standard kétoldali intervallumra és z α z 1 α az alsó vagy felső konfidencia intervallumra. Jegyezzük meg, hogy d determinisztikus, és a standard kétoldali intervallum hossza L 2 d . A d számot néha hibahatárnak hívjuk. Sok esetben a kísérlet megtervezésének első lépése a mintanagyság meghatározása, ami μ becsléséhez szükséges adott hibahatárral és adott konfidencia szinttel.

Mutassuk meg, hogy a szükséges mintanagyság μ becsléséhez 1 α konfidencia szinttel és d hibahatárral

n z α 2 σ 2 d 2

Figyeljük meg, hogy n egyenesen arányos z α 2 -tel és σ 2 -tel és fordítottan arányos d 2 -tel! Ez utóbbi tényből következik, hogy a hibahatár csökkentésekor a csökkenő hozadék elve érvényesül. Például, ha a hibahatárt a felére szeretnénk csökkenteni, akkor a mintanagyságot a négyszeresére kell növelnünk.

Khi-négyzet pivot változón alapuló konfidencia halmazok

A pivot változó

Emlékezzünk vissza, hogy a

W 2 1 n i 1 n X i μ 2

valószínűségi változót néha a minta szórásnégyzet speciális változataként használjuk, mikor az eloszlás μ várható értéke ismert. Másrészt a minta szórásnégyzet szokásos változata (korrigált tapasztalati szórásnégyzet)

S 2 1 n 1 i 1 n X i M 2

Emlékeztetünk arra, hogy a normál minták egyik legfontosabb speciális tulajdonsága az, hogy az M mintaátlag és az S 2 korrigált tapasztalati szórásnégyzet függetlenek. Most legyen

U n σ 2 W 2 ,  V n 1 σ 2 S 2

Mutassuk meg, hogy U felírható az 1. feladatban szereplő alap pivot változók segítségével a lenti módon! Mutassuk meg, hogy ez a változó pivot változó μ σ -ra és khi-négyzet eloszlású n szabadságfokkal!

U i 1 n Z i 2

Mutassuk meg, hogy V U Z 2 . Emiatt V szintén felírható az 1. feladatban szereplő alap pivot változók segítségével, és így pivot változó μ σ -ra és σ -ra. Végül mutassuk meg, hogy ez a változó khi-négyzet eloszlású n 1 szabadságfokkal!

Jelölje g k illetve G k a k szabadságfokú khi-négyzet eloszlás sűrűségfüggvényét illetve eloszlásfüggvényét. Továbbá p 0 1 -re jelölje k p az eloszlás p -ed rendű kvantilisét, azaz definíció szerint k p G k p . k és p kiválasztott értékei esetén a k p -t megkaphatjuk a khi-négyzet eloszlás táblázatából, a kvantilis appletből vagy a legtöbb statisztikai programcsomagból.

Mutassuk meg a következő tulajdonságokat! A (c) részhez használjuk az analízis inverz függvény tételét!

  1. k p 0 , ha p 0
  2. k p , ha p 1
  3. p k p 1 g k k p

U -n alapuló konfidencia halmazok

Használjuk az U pivot változót, hogy megmutassuk, hogy tetszőleges p 0 1 és tetszőleges α 0 1 esetén 1 α szintű konfidencia halmaz μ σ -ra:

U α p μ σ n W 2 μ n 1 p α σ 2 n W 2 μ n α p α

Mutassuk meg, hogy a konfidencia halmaz határoló görbéit a következő egyenlőség adja meg, ahol c a megfelelő khi-négyzet kvantilis! Így a konfidencia halmaz két hiperbola pozitív ága közti régió. Mindkét hiperbola centruma M 0 , ahogy az ábrán látható.

c σ 2 n μ M 2 n 1 S 2
Confidence set

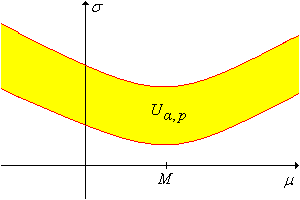
Ahogy eddig, a konfidencia halmaz nem korlátos, ismét nem meglepő módon, mivel két valós paramétert becsültünk egy valós pivot változó segítségével. Viszont, ha μ ismert, a konfidencia halmaz egy korlátos konfidencia intervallum σ 2 -re. Geometriailag ez az intervallum megfelel a függőleges metsző szakasznak μ -nél. Ha a konfidencia korlátok négyzetgyökét vesszük, akkor konfidencia intervallumot kapunk σ -ra. Az a feltételezés, hogy μ ismert, majdnem mindig mesterséges; a konfidencia halmaz, amit a V pivot változó felhasználásával képzünk, konfidencia intervallumhoz vezet σ -ra anélkül, hogy feltételeznénk, hogy μ ismert. Elméletben kaphatunk konfidencia halmazt μ -re, ha feltételezzük, hogy σ ismert; ez a halmaz megfelel a vízszintes metsző szakasznak σ -nál. Jegyezzük meg, hogy általánosságban ez a halmaz nem egy intervallum, hanem két diszjunkt intervallum uniója. Tehát az előző szakaszban leírt konstrukció jobb ilyen esetben.

Tekintsük a 14. feladatban szereplő konfidencia halmazt p 1 illetve p 0 feltétel mellett! Mutassuk meg, hogy a következők 1 α szintű konfidencia halmazok μ σ -ra:

  1. U α 1 μ σ n W 2 μ n 1 α σ 2
  2. U α 0 μ σ 0 σ 2 n W 2 μ n α

Ha μ ismert, akkor az (a) rész 1 α szintű alsó konfidencia korlátot ad σ 2 -re, és a (b) rész 1 α szintű felső konfidencia korlátot ad σ 2 -re.

A 14. feladatban szereplő konfidencia halmazok közül, rögzített konfidencia szint esetén, jobban kedveljük azt, aminek kisebb a nagysága, mivel ez a halmaz adja a legtöbb információt a paraméterekről. Ebben az esetben nem világos, hogyan mérjük a halmaz nagyságát. Amikor μ ismert, természetesen lehetne a mérték a konfidencia intervallum hossza. Jegyezzük meg azonban, hogy ez a hossz véletlen. Ami fontosabb, a hossznak, mint p függvényének, a minimalizálása kiszámítását tekintve nehéz. Mindezen okok miatt, általában az egyenlő-farkú konfidencia halmazt használjuk, ami p 12 -nek felel meg:

U α 1/2 μ σ n W 2 μ n 1 α 2 σ 2 n W 2 μ n α 2

Próbáljuk meg minimalizálni a 14. feladatban szereplő intervallum hosszát, mint p függvényét, rögzített μ esetén!

V -n alapuló konfidencia halmazok

Használjuk a V pivot változót, hogy megmutassuk, hogy tetszőleges p 0 1 és tetszőleges α 0 1 esetén 1 α szintű konfidencia halmaz μ σ -ra:

V α p μ σ n 1 S 2 n 1 1 p α σ 2 n 1 S 2 n 1 α p α
Confidence set

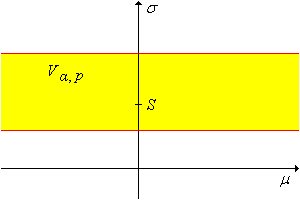
Ez a konfidencia halmaz a konstrukcióból adódóan nem ad információt μ -ről, de σ 2 -re korlátos konfidencia intervallumot biztosít. Ha a konfidencia korlátok négyzetgyökét vesszük, akkor σ -ra kapunk konfidencia intervallumot.

Tekintsük a 18. feladatban szereplő konfidencia halmazt p 1 illetve p 0 feltétel mellett! Mutassuk meg, hogy a következők 1 α szintű konfidencia halmazok μ σ -ra:

  1. V α 1 μ σ n 1 S 2 n 1 1 α σ 2
  2. V α 0 μ σ 0 σ 2 n 1 S 2 n 1 α

Az (a) rész 1 α szintű alsó konfidencia korlátot ad σ 2 -re, és a (b) rész 1 α szintű felső konfidencia korlátot ad σ 2 -re

A 18. feladatban szereplő konfidencia halmazok közül, rögzített konfidencia szint esetén, jobban kedveljük azt, aminek kisebb a nagysága, mivel ez a halmaz adja a legtöbb információt a paraméterekről. Ebben az esetben természetesen mérhetjük a konfidencia halmaz nagyságát a konfidencia intervallum hosszával (a függőleges metsző szakasz). Megjegyezzük, hogy ez a hossz véletlen. Ami fontosabb, a hossznak, mint p függvényének, a minimalizálása kiszámítását tekintve nehéz. Így rendszerint az egyenlő-farkú konfidencia halmazt használjuk, ami p 12 -nek felel meg:

V α 1 2 μ σ n 1 S 2 n 1 1 α 2 σ 2 n 1 S 2 n 1 α 2

Próbáljuk meg minimalizálni a 18. feladatban szereplő intervallum hosszát, mint p függvényét, rögzített μ esetén!

Használjuk a szórásnégyzet becslés kísérletet az eljárás megismerésére! Válasszuk a normál eloszlást! Használjunk különböző paraméterértékeket, konfidencia szintet, mintanagyságot és intervallumtípust! Minden beállítás esetén futtassuk ezerszer a kísérletet, tízes frissítési gyakorisággal! Ahogy fut a szimuláció, figyeljük meg, hogy a konfidencia intervallum akkor és csak akkor tartalmazza a szórást, ha a pivot változó értéke a kvantilesek közt van! Figyeljük meg a konfidencia intervallumok méretét és elhelyezkedését, valamint hogy a sikeres intervallumok aránya hogyan közelíti az elméleti konfidencia szintet!

Student-féle t pivot változón alapuló konfidencia halmazok

A pivot változó

Az utolsó alap konfidencia halmaz esetén megváltoztatjuk a standard normál pivotot, amit először vizsgáltunk, úgy, hogy az eloszlás σ szórását kicseréljük a minta S szórására. Ez μ -re vonatkozó konfidencia intervallumhoz vezet, anélkül a feltételezés nélkül, hogy σ ismert. Szerencsére ez működik a statisztikák néhány speciális tulajdonsága miatt, amikor a minta eloszlása normális. Legyen

T M μ S n

Mutassuk meg, hogy

T Z V n 1

Az előző feladatot felhasználva, mutassuk meg, hogy T felírható az 1. feladatban szereplő alap pivot változók segítségével, és ezen változó eloszlása Student-féle t eloszlás n 1 szabadságfokkal! Így ez a változó pivot változó μ σ -ra és egyedül μ -re is.

k 0 esetén jelölje φ k illetve Φ k a k szabadságfokú t -eloszlás sűrűségfüggvényét illetve eloszlásfüggvényét. Továbbá p 0 1 esetén jelölje t k p az eloszlás p -ed rendű kvantilisét, azaz t k p Φ k p . k és p rögzített értékei esetén t k p értékei megkaphatók a t eloszlás táblázatból vagy a kvantilis appletből.

Mutassuk meg a következő tulajdonságokat! A (d) rész az analízis inverz függvény tételéből következik.

  1. t k p t k 1 p
  2. t k p , ha p 0
  3. t k p , ha p 1
  4. t k p 1 φ k t k p

Konfidencia halmazok

Mutassuk meg, hogy tetszőleges p 0 1 és α 0 1 esetén 1 α szintű konfidencia intervallum μ σ -ra:

T α p μ σ M t n 1 1 p α S n μ M t n 1 α p α S n
Confidence set

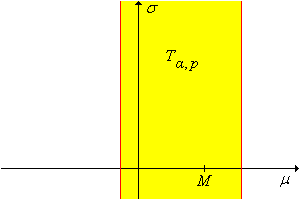
Ez a konfidencia halmaz a konstrukcióból adódóan nem ad információt σ -ról, de μ -re korlátos konfidencia intervallumot biztosít. A konfidencia halmaz világosan mérhető L -lel, a vízszintes metsző szakasz hosszával, vagy ekvivalensen a μ -re vonatkozó konfidencia intervallum hosszával.

Mutassuk meg, hogy L t n 1 1 p α t n 1 α p α S n . Megjegyezzük, hogy L véletlen. Mutassuk meg, hogy

  1. L α csökkenő függvénye rögzített n és p esetén!
  2. L 0 , ha α 1 és L , ha α 0 rögzített n és p esetén!
  3. L n csökkenő függvénye rögzített α és p esetén!
  4. L 0 , ha n rögzített α és p esetén!
  5. L szimmetrikus p 12 -re rögzített n és α esetén!
  6. L csökkenő, ha p növekszik 0-tól 12 -ig és L növekvő, ha p növekszik 12 -től 1-ig rögzített n , α és σ esetén!
  7. L minimális, amikor p 12 rögzített n és α esetén!
  8. L , ha p 0 , és ha p 1 rögzített n és α esetén!

A 26. feladat ismét rámutat arra, hogy a konfidencia szint és a konfidencia halmaz mérete közt kompromisszum van. Ha n és p rögzítettek, csak a becslés konfidencia szintjének csökkentése árán csökkenthetjük L -et és javíthatjuk a becslésünket. Fordítva, csak a halmaz méretének növelése árán növelhetjük a becslésünk konfidencia szintjét. p -t tekintve, az 1 α szintű kétoldali konfidencia halmazok közül a legjobb (és a mindig használt) az egyenlő-farkú halmaz:

T α 1 2 μ σ M t n 1 1 α 2 S n μ M t n 1 1 α 2 S n

Ez a halmaz egyenlő-farkú konfidencia intervallumot ad μ -re. Megjegyezzük, hogy ez az intervallum szimmetrikus az M mintaátlagra, de az intervallum hossza ismét véletlen.

Tekintsük a 25. feladatban szereplő konfidencia halmazt p 1 illetve p 0 esetén! Mutassuk meg, hogy a következők 1 α szintű konfidencia halmazok μ σ -ra:

  1. T α 1 μ σ M t n 1 1 α S n μ
  2. T α 0 μ σ μ M t n 1 1 α S n

Az (a) rész 1 α szintű alsó konfidencia korlátot ad μ -re, és a (b) rész 1 α szintű felső konfidencia korlátot ad μ -re.

Használjuk az átlag becslés kísérletet az eljárás megismerésére! Válasszunk normál eloszlást és Student pivotot! Használjunk különböző paraméterértékeket, konfidencia szintet, mintanagyságot és intervallumtípust! Minden beállítás esetén futtassuk ezerszer a kísérletet, tízes frissítési gyakorisággal! Ahogy fut a szimuláció, figyeljük meg, hogy a konfidencia intervallum akkor és csak akkor tartalmazza az átlagot, ha a pivot változó értéke a kvantilesek közt van! Figyeljük meg a konfidencia intervallumok méretét és elhelyezkedését, valamint hogy a sikeres intervallumok aránya hogyan közelíti az elméleti konfidencia szintet!

Metszetek

A következőkben a fent konstruált konfidencia halmazok felhasználásával metszeteket képzünk, hogy korlátos konfidencia halmazokat nyerjünk μ σ -ra. Azt a tényt fogjuk felhasználni, hogy az M mintaátlag és az S 2 korrigált tapasztalati szórásnégyzet függetlenek, ami a normál minták egyik legfontosabb speciális tulajdonsága. Szükségünk lesz még az 1. feladatra a Bevezetésből, ami Bonferroni egyenlőtlenségen alapul. A következő feladatokban tegyük fel, hogy α β p q 0 1 4 és α β 1 .

Mutassuk meg, hogy az alábbi halmazok konzervatív 1 α β szintű konfidencia halmazok μ σ -ra:

  1. Z α p U β q
  2. T α p V β q
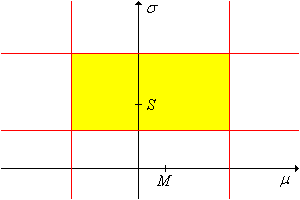
Confidence set Confidence set

Használjuk a függetlenséget, hogy megmutassuk, hogy Z α p V β q egy 1 α 1 β szintű konfidencia halmaz μ σ -ra! Ez egy ék alakú konfidencia halmaz, ahogy a lenti ábrán is látható.

Confidence set

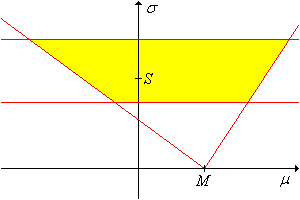
Érdekes megjegyezni, hogy a 29(b) feladatban szereplő konfidencia halmaz egy szorzathalmaz, mint a paramétertér egy részhalmaza, de nem szorzathalmaz, mint a mintatér részhalmaza. Ellenkezőleg, a 30. feladatban szereplő konfidencia halmaz nem szorzathalmaz, mint a paramétertér egy részhalmaza, de szorzathalmaz, mint a mintatér egy részhalmaza.

Feladatok

Robusztosság

Az alapfeltevésünk az volt, hogy a megalapozó minta eloszlása normális. Természetesen valós statisztikai problémák esetén valószínűtlen, hogy sokat tudunk a minta eloszlásáról, még arról sem, hogy vajon normális-e. Amikor egy statisztikai eljárás meglehetősen jól működik, még ha a megalapozó feltevések nem is teljesülnek, az eljárást robusztusnak hívjuk. Ebben az alfejezetben μ és σ becslési eljárásainak robusztusságát fogjuk megvizsgálni.

Tegyük fel, hogy a tényleges eloszlás nem normális. Amikor az n mintanagyság elég nagy, a mintaátlag eloszlása közelítően normális lesz a centrális határeloszlás tétel szerint. Így a μ -re vonatkozó intervallumbecslésünk közelítően érvényes lehet.

Használjuk az átlag becslés kísérletet az eljárás megismerésére! Válasszunk gamma eloszlást és Student pivotot! Használjunk különböző paraméterértékeket, konfidencia szintet, mintanagyságot és intervallumtípust! Minden beállítás esetén futtassuk ezerszer a kísérletet, tízes frissítési gyakorisággal! Figyeljük meg a konfidencia intervallumok méretét és elhelyezkedését, valamint hogy a sikeres intervallumok aránya hogyan közelíti az elméleti konfidencia szintet!

Az átlag becslés kísérletben ismételjük meg az előző gyakorlatot egyenletes eloszlással!

Hogy milyen nagy n szükséges ahhoz, hogy a μ -re vonatkozó intervallum becslési eljárás jól működjön, természetesen függ az alap eloszlástól; minél inkább eltér ez az eloszlás a normálistól, annál nagyobb n szükséges. Szerencsére a normálishoz tartó konvergencia gyors a centrális határeloszlás tétel szerint, és így, ahogy a gyakorlatban megfigyelhettük, viszonylag kis mintanagysággal (30 vagy több) is célt érhettünk a legtöbb esetben.

Általánosságban, a σ -ra vonatkozó intervallum becslési eljárások nem olyan robusztusak, mint a μ -re vonatkozók.

A szórásnégyzet becslés kísérletben válasszuk a gamma eloszlást! Használjunk különböző paraméterértékeket, konfidencia szintet, mintanagyságot és intervallumtípust! Minden beállítás esetén futtassuk ezerszer a kísérletet, tízes frissítési gyakorisággal! Figyeljük meg a konfidencia intervallumok méretét és elhelyezkedését, valamint hogy a sikeres intervallumok aránya hogyan közelíti az elméleti konfidencia szintet!

A szórásnégyzet becslés kísérletben válasszuk az egyenletes eloszlást! Használjunk különböző paraméterértékeket, konfidencia szintet, mintanagyságot és intervallumtípust! Minden beállítás esetén futtassuk ezerszer a kísérletet, tízes frissítési gyakorisággal! Figyeljük meg a konfidencia intervallumok méretét és elhelyezkedését, valamint hogy a sikeres intervallumok aránya hogyan közelíti az elméleti konfidencia szintet!

Számítási feladatok

A következő feladatokban a kétoldali konfidencia intervallumok esetén konstruáljunk egyenlő-farkú intervallumot, hacsak a feladat mást nem mond!

Egy bizonyos gépalkatrész hossza 10 centiméter elméletileg, de a gyártási folyamat tökéletlensége miatt a tényleges hossz normális eloszlású μ várható értékkel és σ 2 szórásnégyzettel. A szórásnégyzet a folyamat sajátosságai miatt nem változik az idők során. Történeti adatokból tudjuk, hogy σ 0.3 . Másrészt μ különböző gyártási paraméterek módosításával befolyásolható, és így elég gyakran változhat valamilyen ismeretlen értékre. Egy 100 elemű mintára az átlag 10,2.

  1. Készítsünk 95%-os konfidencia intervallumot μ -re!
  2. Konstruáljunk 95%-os felső konfidencia korlátot μ -re!
  3. Konstruáljunk 95%-os alsó konfidencia korlátot μ -re!

Tegyük fel, hogy egy zacskó csipsz tömege (grammban) normális eloszlású valószínűségi változó μ várható értékkel és σ szórással, mindkettő ismeretlen. Egy 75 elemű mintára az átlag 250 és a szórás 10.

  1. Konstruáljunk 90%-os konfidencia intervallumot μ -re!
  2. Konstruáljunk 90%-os konfidencia intervallumot σ -ra!
  3. Konstruáljunk egy konzervatív 90%-os konfidencia téglalapot μ σ -ra!

Egy telemarketing cégnél a telefonos kérelem hossza (másodpercekben) normális eloszlású valószínűségi változó μ várható értékkel és σ szórással, mindkettő ismeretlen. Egy 50 hívást tartalmazó minta alapján az átlag 300 és a szórás 60.

  1. Konstruáljunk 95%-os felső konfidencia korlátot μ -re!
  2. Konstruáljunk 95%-os alsó konfidencia korlátot σ -ra!

Egy bizonyos farmon az őszibarack tömege szüret idején (unciában) normális eloszlású valószínűségi változó, melynek szórása 0,5. Hány darab őszibarackot kell mintavételezni, hogy az átlagtömeget 0,2 hibahatárral és 95%-os konfidencia szinten meg tudjuk becsülni?

Egy bizonyos típusú építési munkán az órabér normális eloszlású valószínűségi változó 1,25 dollár szórással és ismeretlen μ várható értékkel. Hány munkást kell mintavételezni, hogy 95%-os alsó konfidencia korlátot konstruálhassunk μ -re 0,25 dollár hibahatárral?

A Michelson adatok esetén tegyük fel, hogy a mért fénysebesség normális eloszlású μ várható értékkel és σ szórással, mindkettő ismeretlen.

  1. Konstruáljunk 95%-os konfidencia intervallumot μ -re! Benne van-e a fénysebesség valódi értéke ebben az intervallumban?
  2. Konstruáljunk 95%-os konfidencia intervallumot σ -ra!
  3. Vizsgáljuk meg grafikusan a feltevést, hogy a megalapozó eloszlás normális!

A Cavendish adatok esetén tegyük fel, hogy a mért sűrűségadatok (a Föld sűrűsége) normális eloszlásúak μ várható értékkel és σ szórással, mindkettő ismeretlen.

  1. Konstruáljunk 95%-os konfidencia intervallumot μ -re! Benne van-e a Föld sűrűségének valódi értéke ebben az intervallumban?
  2. Konstruáljunk 95%-os konfidencia intervallumot σ -ra!
  3. Vizsgáljuk meg grafikusan a feltevést, hogy a meglapozó eloszlás normális!

A Short adatok esetén tegyük fel, hogy a Nap mért parallaxis adatai normális eloszlásúak μ várható értékkel és σ szórással, mindkettő ismeretlen.

  1. Konstruáljunk 95%-os konfidencia intervallumot μ -re! Benne van-e a Nap parallaxisának valódi értéke ebben az intervallumban?
  2. Konstruáljunk 95%-os konfidencia intervallumot σ -ra!
  3. Vizsgáljuk meg grafikusan a feltevést, hogy a meglapozó eloszlás normális!

Tegyük fel, hogy az írisz egy adott fajtájának (Setosa, Verginica vagy Versicolor) sziromhossza normális eloszlású. Használjuk a Fisher írisz adatokat, hogy 90%-os kétoldali konfidencia intervallumot konstruáljunk a következő paraméterekre:

  1. átlagos sziromhossz Sertosa írisz esetén!
  2. átlagos sziromhossz Vergnica írisz esetén!
  3. átlagos sziromhossz Versicolor írisz esetén!

  1. Virtual Laboratories
  2. 7. Intervallumbecslés
  3. 1
  4. 2
  5. 3
  6. 4
  7. 5