A state in a Markov chain is periodic if the chain can return to the state only at multiples of some integer larger than 1. Periodic behavior complicates the study of the limiting behavior of the chain. As we will see in this section, we can eliminate the periodic behavior by considering the -step chain, where is the period, but only at the expense of introducing additional equivalence classes. Thus, in a sense, we can trade one form of complexity for another.
As usual, our starting point is a (time homogeneous) Markov chain with countable state space and transition probability matrix . The period of state is
Thus, starting in , the chain can return to only at multiples of the period , and is the largest such integer. State is aperiodic if and periodic if . Perhaps the most important result is that period, like recurrence and transience, is a class property.
Show that if then .
Thus, the definitions of period, periodic, and aperiodic apply to equivalence classes as well as individual states. When the chain is irreducible, we can apply these terms to the entire chain.
Suppose that .
Suppose now that is irreducible and is periodic with period . There is no real loss in generality in assuming that the chain is irreducible, for if this were not the case, we could simply restrict our attention to one of the closed, irreducible equivalence classes. Now, we fix a reference state , and for , define
Suppose that and are indices in . Show that and if and only if for some .
Show that are the equivalence classes for the -step to and from relation that governs the -step chain that has transition matrix
In particular, partitions the state space ; these sets are known as the cyclic classes. The basic structure of the chain is shown in the state diagram below:
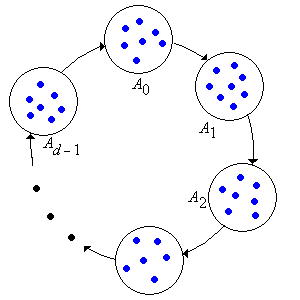
Consider the Markov chain with state space and transition matrix given below:
Review the definition of the basic Ehrenfest chain. Show that this chain has period 2, and find the cyclic classes.
Review the definition of the modified Ehrenfest chain. Show that this chain is aperiodic.
Review the definition of the simple random walk on . Show that the chain is periodic with period 2, and find the cyclic classes.