The study of Markov chains, particularly the limiting behavior, depends critically on the random times between visits to a given state. The nature of this random times leads to a fundamental dichotomy of the states.
As usual, our starting point is a (time homogeneous) Markov chain with state space and transition probability matrix .
Let be a nonempty subset of . Recall that the hitting time to is the random variable that gives the first positive time that the chain is in :
Since the chain may never enter , the random variable takes values in . When , we will simplify the notation to . This random variable gives the first positive time that the chain is in state . Now for and , let
Note that
Again, when , we will simplify the notation to and , respectively. In particular, is the probability, starting at , that the chain eventually returns to . If , is the probability, starting at , that the chain eventually reaches . Just knowing when is 0, positive, and 1 will turn out to be of considerable importance in the overall structure and limiting behavior of the chain. As a function on , we will refer to as the hitting matrix of .
Show that if and only if for some .
The following exercise gives a basic relationship between the sequence of hitting probabilities and the sequence of transition probabilities.
Suppose that . Condition on to show that
Starting in state , the chain is in state at time if and only if the chain hits for the first time at some previous time , and then returns to in the remaining steps.
Suppose that and . Condition on to show that
Starting in state , the chain first enters at time if and only if the chain goes to some state at time 1, and then from state , first enters in steps. Similarly, starting in state , the chain eventually enters if and only if it either enters at the first step, or moves to some other state at the first step, and then eventually enters from .
A state is said to be recurrent if and is said to be transient if . Thus, starting in a recurrent state, the chain will, with probability 1, eventually return to the state. As we will see, the chain will return to the state infinitely often with probability 1, and the times of the visits will form the arrival times of a renewal process. This will turn out to be the critical observation in the study of the limiting behavior of the chain. By contrast, if the chain starts in a transient state, then there is a positive probability that the chain will never return to the state.
Again, suppose that is a nonempty set of states. A natural complement to the hitting time to is the counting variable that gives the number of visits to (at positive times). Thus, let
We will mostly be interested in the special case , and in this case, we will simplify the notation to . Note that takes value in .
Let for and . Show that
Consistent with our notation in the Introduction, is a transition measure on (although, of course, not a transition probability measure). Show that
The matrix is known as the potential matrix. (Some authors count the state at time 0 and thus the index in the definition of the counting variable and in Exercise 5 starts at 0 rather than 1.)
The distribution of has a simple representation in terms of the hitting probabilities. Note that because of the Markov property and time homogenous property, whenever the chain reaches state , the future behavior is independent of the past and is stochastically the same as the chain starting in state at time 0. This is the critical observation in the proof of the following exercise.
Suppose that and are states. Show that
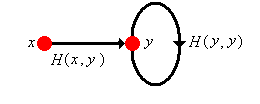
The essence of the proof is illustrated in the graphic above. The thick lines are intended as reminders that these are not one step transitions, but rather represent all paths between the given vertices. Note that in the special case that we have
In all cases, the counting variable has essentially a geometric type distribution, but the distribution may well be defective, with some of the probability mass at . The behavior is quite different depending on whether is transient or recurrent.
Suppose that and are states and that is transient. Show that
Suppose that and are states and that is recurrent. Show that
Note that there is an invertible relationship between the hitting probability matrix and the potential matrix ; if we know one we can compute the other. In particular, we can characterize the transience or recurrence of a state in terms of :
The hitting probabilities lead to an important relation on the state space . For , we say that leads to and we write if either or . It follows immediately from Exercise 2 that if and only if for some . In terms of the graph of the chain, if and only if there is a directed path from to . Note that the leads to relation is reflexive by definition: for any .
Show that the leads to relation is transitive: if and then .
A nonempty set of states is closed if and implies . A closed set is irreducible if has no proper closed subset.
Suppose that is closed.
Of course, the entire state space is closed by definition. If it is also irreducible, we say the Markov chain is irreducible.
Suppose that is a nonempty subset of . Show that is the smallest closed set containing , and is called the closure of . That is, show that
Recall that for a fixed positive integer , is also a transition probability matrix, and in fact governs the -step Markov chain. . It follows that we could consider the leads to relation for this chain, and all of the results above would still hold (relative, of course to the -step chain). Occasionally we will need to consider this relation, which we will denote by , particularly in our study of periodicity.
Suppose that and are positive integers. Show that if and . then .
By combining the leads to relation with its inverse, the comes from relation , we can obtain another very useful relation. For , we say that to and from and we write if and . By definition, this relation is symmetric: if then . From our work above, it is also reflexive and transitive. Thus, the to and from relation is an equivalence relation. Like all equivalence relations, it partitions the space into mutually disjoint equivalence classes. We will denote the equivalence class of a state by
Thus, for any two states and , either or , and moreover,
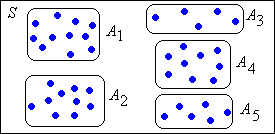
Draw state graphs to illustrate the following facts:
On the other hand, show that if is a closed, irreducible set of states, then is an equivalence class.
The to and from equivalence relation is very important because many interesting state properties turn out in fact to be class properties, shared by all states in a given equivalence class. In particular, the recurrence and transience properties are class properties.
The following exercise gives the fundamental result of this section: a recurrent state can only lead to other recurrent states.
Suppose that is a recurrent state and that . Show that is recurrent and that .
From the last exercise, note that if is recurrent, then all states in the equivalence class of are also recurrent. Thus, for each equivalence class, either all states are transient or all states are recurrent. We can therefore refer to transient or recurrent classes as well as states.
Suppose that is a recurrent equivalence class. Show that is closed and irreducible.
Suppose that is finite and closed. Show that has a recurrent state.
Suppose that is finite, closed, and irreducible. Show that is a recurrent equivalence class.
Thus, the Markov chain will have a collection (possibly empty) of recurrent equivalence classes where is a countable index set. Each is closed and irreducible. Let denote the set of all transient states. The set may be empty or may consist of a number of equivalence classes, but the class structure of is not important to us. If the chain starts in for some then the chain remains in forever, visiting each state infinitely often with probability 1. If the chain starts in , then the chain may stay in forever (but only if is infinite) or may enter one of the recurrent classes , never to escape. However, in either case, the chain will visit a given transient state only finitely many time with probability 1. This basic structure is known as the canonical decomposition of the chain, and is shown in graphical form below. The edges from are in gray to indicate that these transitions may not exist.
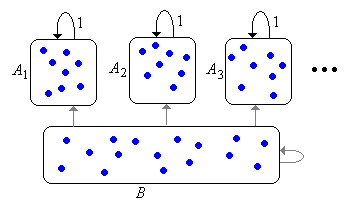
Suppose that is a proper subset of .
The staying probability function is an interesting complement to the hitting matrix studied above. The following exercise characterizes this function and provides a method that can be used to compute it, at least in some cases.
Show that is the largest function on that takes values in and satisfies . Moreover, either or
Note that the characterization in the last exercise includes a zero-one law of sorts: either the probability that the chain stays in forever is 0 for every initial state , or we can find states for which the probability is arbitrarily close to 1. The next two exercises explore the relationship between the staying function and recurrence.
Suppose that is an irreducible, recurrent chain with state space . Show that for any proper subset of .
Suppose that is an irreducible Markov chain with state space and transition probability matrix . Show that if there exists a state such that where then is recurrent.
More generally, suppose that is a Markov chain with state space and transition probability matrix . The last two exercise can be used to test whether a closed, irreducible equivalence class is recurrent or transient. We fix a state and set . We then try to solve the equation on . If the only solution taking values in is , then the class is recurrent by Exercise 23. If there are nontrivial solutions, then is transient by Exercise 22. Often we try to choose to make the computations easy.
We now know quite a bit about Markov chains, and we can often classify the states and compute quantities of interest. However, we do not yet know how to compute:
These problems are related, because of the general inverse relationship between the hitting matrix and the potential matrix noted in our discussion above. As usual, suppose that is a Markov chain with state space , and let denote the set of transient states. The next exercise shows how to compute , the potential matrix restricted to the transient states. Recall that the values of this matrix are finite.
Show that satisfies the equation and is the smallest nonnegative solution. If is finite, .
Now that we can compute , we can also compute using the result in Exercise 8. All that remains is for us to compute the hitting probability when is transient and is recurrent. The first thing to notice is that the hitting probability is a class property.
Suppose that is transient and that is a recurrent class. Show that for . That is, the hitting probability to is constant for , and is just the hitting probability to the class .
As before, let denote the set of transient states and suppose that is a recurrent equivalence class. Let denote the function on that gives the hitting probability to class , and let denote the function on that gives the probability of entering on the first step:
Show that .
The result in the last exercise is adequate if we have already computed (using the result in Exercise 24, for example). However, we might just want to compute directly.
Show that satisfies the equation and is the smallest nonnegative solution. If is finite, .
Consider a Markov chain with state space and transition matrix given below:
Consider a Markov chain with state space and transition matrix given below:
Consider a Markov chain with state space and transition matrix given below:
Read again the definitions of the Ehrenfest chains and the Bernoulli-Laplace chains. Note that since these chains are irreducible and have finite state spaces, they are recurrent.
Read the discussion on recurrence in the section on the reliability chains and work the exercises.
Read the discussion on random walks on in the section on the random walks on graphs and work the exercises.
Read the discussion on extinction and explosion in the section on the branching chain and work the exercises.
Read the discussion on recurrence and transience in the section on queuing chains and work the exercises.
Read the discussion on recurrence and transience in the section on birth-death chains and work the exercises.