Reliability Chains

Suppose that we have a sequence of trials, each of which results in either success or failure. Our basic assumption is that if there have been

x

consecutive successes, then the probability of success on the next trial is

p x

where

p 01

. Whenever there is a failure, we start over, independently, with a new sequence of trials. Appropriately enough,

p

is called the success function. Let

X n

denote the length of the run of successes after

n

trials.

Argue that $X X 0 X 1 X 2$ is a Markov chain with state space and transition probability function

P x x 1 p x, P x 0 1 p x, x

This Markov chain is called the success-runs chain. The state graph of is given below:

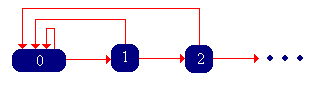
Now let

T

denote the trial number of the first failure, starting with a fresh sequence of trials. Note that in the context of the success-runs chain

X

T T 0

, the first return time to state 0, starting in 0. Note that

T

takes values in

, since, presumably, it is possible that no failure occurs. Let

r n T n

for

n

, the probability of at least

n

consecutive successes, starting with a fresh set of trials. Let

f n T n

for

n

, the probability of exactly

n 1

, consecutive successes, starting with a fresh set of trails.

Show that

$p x r x 1 r x$ for $x$
$r n x 0 n 1 p x$ for $n$
$f n 1 p n 1 x 0 n 2 p x$ for $n$
$r n 1 x 1 n f x$ for $n$
$f n r n 1 r n$ for $n$

Thus, the functions

p

r

, and

f

give equivalent information. If we know one of the functions, we can construct the other two, and hence any of the functions can be used to define the success-runs chain.

The function $r$ is the reliability function associated with $T$ . Show that it is characterized by the following properties:

$r$ is positive.
$r 0 1$
$r$ is strictly decreasing.

Show that the function $f$ is characterized by the following properties:

$f$ is positive.
$x 1 f x 1$

Essentially,

f

is the probability density function of

T

, except that it may be defective in the sense that the sum of its values may be less than 1. The leftover probability, of course, is the probability that

T

. This is the critical consideration in the classification of the success-runs chain, which we consider in the next paragraph.

Verify that each of the following functions has the appropriate properties, and then find the other two functions:

$p$ is a constant in $01$ . Thus, the trials are Bernoulli trials.
$r n 1 n 1$ for $n$ .
$r n n 1 2 n 1$ for $n$ .
$p x 1 x 2$ for $x$ .

The success-runs applet is a simulation of the success-runs chain based on Bernoulli trials. Run the simulation 1000 times for various values of $p$ , and note the limiting behavior of the chain.

Recurrence and the Remaining Life Chain

From the state graph, show that the success-runs chain is irreducible and aperiodic.

Recall that

T

has the same distribution as the first return time to 0 starting at state 0. Thus, the classification of the chain as recurrent or transient depends on

α T

. Specifically, the success-runs chain is transient if

α 0

and recurrent if

α 0

. Thus, we see that the chain is recurrent if and only if a failure is sure to occur. We can compute the parameter

α

in terms of each of the three functions that define the chain.

Show that

α x 0 p x n r n 1 x 1 f x

When the success-runs chain

X

is recurrent, we can define a related random process. Let

Y n

denote the number of trials remaining until the next failure, after

n

trials.

Argue that $Y Y 0 Y 1 Y 2$ is a Markov chain with state space and transition probability function

Q 0 x f x 1, Q x 1 x 1, x

The Markov chain $Y$ is called the remaining life chain. Verify the state graph below and show that this chain is also irreducible, aperiodic, and recurrent.

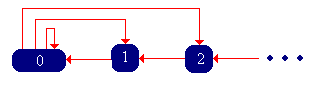
Compute $α$ and determine whether the success-runs chain $X$ is transient or recurrent for each of the cases in Exercise 5.

Run the simulation of the success-runs chain 1000 times for various values of $p$ , starting in state 0. Note the return times to state 0.

Positive Recurrence and Limiting Distributions

Let

μ T

, the expected trial number of the first failure, starting with a fresh sequence of trials.

Show that the success-runs chain $X$ is positive recurrent if and only if $μ$ , in which case the invariant distribution has probability density function $g$ given by

g x r x μ, x

Show that

If $α 0$ then $μ$
If $α 0$ then $μ n 1 n f n$
$μ n 0 r n$

Suppose that $α 0$ , so that the remaining life chain $Y$ is well-defined. Show that this chain is also positive recurrent if and only if $μ$ , with the same invariant distribution as $X$ (with probability density function $g$ given in the previous exercise).

Determine whether the success-runs chain $X$ is transient, null recurrent, or positive recurrent for each of the cases in Exercise 5. If the chain is positive recurrent, find the invariant probability density function.

The success-runs chain corresponding to Bernoulli trials has a geometric distribution as the invariant distribution. Run the simulation of the success-runs chain 1000 times for various values of $p$ . Note the apparent convergence of the empirical distribution to the invariant distribution.

Time Reversal

Suppose that

μ

, so that the success-runs chain

X

and the remaining-life chain

Y

are positive recurrent.

Show that $X$ and $Y$ are time reversals of each other, and use this fact to show again that $g$ is the invariant probability density function.

Run the simulation of the success-runs chain 1000 times for various values of $p$ , starting in state 0. If you imagine watching the simulation backwards in time, then you can see a simulation of the remaining life chain.

8. Reliability Chains

The Success-Runs Chain

Recurrence and the Remaining Life Chain

Positive Recurrence and Limiting Distributions

Time Reversal