Konvergencia

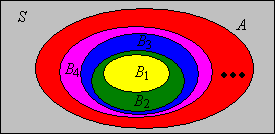
Ebben a fejezetben a korábbiaknál kicsit mélyebb fogalmakkal ismerkedünk meg. Azonban ezek is nagyon fontosak, speciálisan a következő témákhoz elengedhetetlenek:

A folytonossági tétel

Növekvő események

Események egy

A 1 A 2

sorozatát növekvőnek nevezzük, ha

A n A n 1

minden

n

-re. Tehát az események növekvőek, a szokásos részben rendezésre nézve (egy halmaz nagyobb a valódi részhalmazainál). A növekvő kifejezést a megfelelő indikátor változókra is használhatjuk.

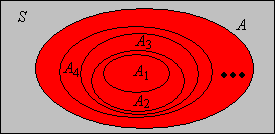
Legyen $I n$ az $A n$ esemény indikátor változója, amint $n$ . Igazoljuk, hogy az események pontosan akkor növekedők, ha a hozzájuk tartozó indikátor változók növekedőek a szokásos értelemben, azaz $I n I n 1$ minden $n$ -re.

A 1 A 2

növekvő események sorozata, akkor az uniójukat úgy is nevezhetjük, hogy a limeszük:

Mint az előbb, a limesz elnevezés az indikátor változókkal történő megfeleltetésből adódik:

Legyenek $A 1 A 2$ növekvő események, és legyen $I n$ az $A n$ esemény indikátor valószínűségi változója ( $n$ ), és jelölje $I$ az unió indikátor változóját. Igazoljuk, hogy

n I n I .

Általában egy függvényt akkor szokás folytonosnak nevezni, ha jól viselkedik a határértékek mentén. Ezért a következő feladatban bizonyítandó állítást úgy nevezik, hogy növekvő eseményekre vonatkozó folytonossági tétel:

Legyenek $A 1 A 2$ növekvő események. Igazoljuk, hogy

n A n n A n .

Legyen $B 1 A 1$ és $B i A i A i 1$ amint $i 23$ .
Igazoljuk, hogy $B 1 B 2$ páronként diszjunkt események, és az uniójuk megegyezik az $A 1 A 2$ halmazok uniójával!
A valószínűségszámítás additivitási axiómájának segítségével igazoljuk az állítást!

The construction in the continuity theorem

A következő feladat arra mutat rá, hogy tetszőleges események uniója felírható növekvő események uniójaként.

Legyen $A 1 A 2$ tetszőleges események sorozata. Igazoljuk, hogy

$i 1 n A i$ növekvő $n$ -ben
$n i 1 n A i i 1 A i$
$n i 1 n A i i 1 A i .$

Legyen $A$ az alapkísérletünktől függő esemény, melyre $A 0$ . Igazoljuk, hogy abban az összetett kísérletben, mely az alapkísérlet ismételgetéséből áll, annak a valószínűsége, hogy $A$ valaha bekövetkezik éppen 1.

Csökkenő események

A 1 A 2

eseménysorozatot csökkenőnek nevezzük, ha

A n 1 A n

minden

n

-re. Tehát az események csökkenőek a szokásos rendezésre (lásd fent) nézve. A csökkenő kifejezést a megfelelő indikátor változókra is használják:

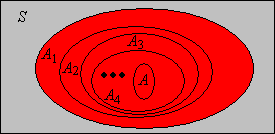
Legyen $I n$ az $A n$ esemény indikátor valószínűségi változója ( $n$ ). Igazoljuk, hogy az események pontosan akkor csökkenőek, ha a megfelelő indikátor függvények csökkenőek a szokásos értelemben, azaz $I n 1 I n$ minden $n$ -re.

A 1 A 2

csökkenő események sorozata, akkor a metszetüket úgy is nevezhetjük, hogy a limeszük:

Mint az előbb, a limesz elnevezés az indikátor változókkal történő megfeleltetésből adódik:

Tegyük fel, hogy $A 1 A 2$ csökkenő események. Legyen $I n$ az $A n$ esemény indikátor valószínűségi változója, amint $n$ , és legyen $I$ az események metszetének indikátor változója. Igazoljuk, hogy

n I n I .

A következő feladat állítása a csökkenő események folytonossági tétele:

Tegyük fel, hogy $A 1 A 2$ csökkenő események. Igazoljuk, hogy

n A n n A n .

Igazoljuk, hogy az $A 1 > A 2$ események növekvőek.
Alkalmazzuk a folytonossági tételt az (a) feladatban szereplő eseményekre!
Használjuk a De Morgan szabályt és a komplementer képzésre vonatkozó szabályt!

A következő feladat arra mutat rá, hogy tetszőleges események metszete felírható csökkenő események metszeteként.

Legyn $A 1 A 2$ tetszőleges eseményeksorozata. Igazoljuk, hogy

$i 1 n A i$ csökkenő $n$ -ben!
$n i 1 n A i i 1 A i$
$n i 1 n A i i 1 A i .$

A Borel-Cantelli lemmák

Az első lemma

Igazoljuk, hogy $i n A i$ csökkenő az $n$ függvényében.

Az előző csökkenő sorozat limesze, azaz metszete az eredeti sorozat limesz szuperiorja.

Igazoljuk, hogy $n A n$ az az esemény, amely pontosan akkor következik be, ha $A n$ végtelen sok $n$ -re bekövetkezik!

Mint azt már megszokhattuk, az elnevezés az indikátor változókkal történő megfeleltetésből adódik:

Legyen $I n$ az $A n$ esemény indikátor valószínűségi változója ( $n$ ), és legyen $I$ az $n A n$ esemény indikátor változója. Igazoljuk, hogy

I n I n .

A csökkenő eseményekre vonatkozó folytonossági tétellel igazoljuk, hogy

n A n n i n A n .

A következő feladat állítása az első Borel-Cantelli lemma, amelyet Emil Borel-ről és Francessco Cantelli-ról neveztek el. Ez egy elégséges feltétel arra, hogy végtelen sok esemény 0 valószínűséggel következzen be.

Igazoljuk, hogy ha $n 1 A n$ , akkor $n A n 0$ .

Használjuk az előző feladat eredményét!
Alkalmazzuk a Boole egyenlőtlenséget!
Használjuk azt az egyszerű állítást, hogy ha egy végtelen sor konvergens, akkor a sorozat farka tart a nullához.

A második lemma

Igazoljuk, hogy $i n A i$ növekvő $n$ -ben!

Az előző növekvő sorozat limesze, azaz uniója az eredeti sorozat limesz inferiorja.

Igazoljuk, hogy $n A n$ az az esemény, amely pontosan akkor következik be, ha az $A n$ véges sok $n$ kivételével bekövetkezik.

Mint azt már megszokhattuk, az elnevezés az indikátor változókkal történő megfeleltetésből adódik:

Legyen $I n$ az $A n$ esemény indikátor valószínűségi változója ( $n$ ), és legyen $I$ az $n A n$ esemény indikátor változója. Igazoljuk, hogy

I n I n .

A csökkenő eseményekre vonatkozó folytonossági tétel segítségével igazoljuk, hogy

n A n n i n A i .

Igazoljuk, hogy $n A n n A n$ .

A De Morgan azonosság felhasználásával igazoljuk, hogy $n A n n A n$ .

A következő feladat állítása a második Borel-Cantelli lemma, amely egy elégséges feltétel arra, hogy végtelen sok esemény 1 valószínűséggel következzen be.

Tegyük fel, hogy $A 1 A 2$ független események sorozata. Igazoljuk, hogy ha $n 1 A n$ , akkor $n A n 1$ .

Igazoljuk, hogy $1 x x$ minden $x$ esetén!
Lássuk be, hogy $1 A k A k$ minden $k$ -ra!
Használjuk az előző feladat eredményét, és a függetlenséget!

Legyen $A$ egy az alapkísérlettől függő esemény, amelyre $A 0$ . Igazoljuk, hogy abban az összetett kísérletben, mely az alapkísérletünk ismételgetéséből áll, az $A$ végtelen sokszor bekövetkezik esemény egy valószínűségű!

Tegyük fel, hogy adott pénzérméknek egy természetes számokkal indexelt végtelen sorozata. Továbbá az $n$ -edik pénzérme feldobása után a fej valószínűsége $1 n a$ minden $n$ -ra, ahol $a 0$ paraméter. Minden érmét feldobunk pontosan egyszer. $a$ függvényében határozzuk meg a következő események valószínűségét:

végtelen sok fejet dobunk.
végtelen sok írást dobunk.

Valószínűségi változók konvergenciája

Tegyük fel, hogy

X 1 X 2

és

X

egy véletlen kísérlettel kapcsolatos valós értékű valószínűségi változók. Kétféleképp fogjuk definiálni azt, hogy az

X n

sorozat konvergál

X

-hez amint

n

. Ezek azért is nagyon fontos alapfogalmak, mert a valószínűségszámítás legizgalmasabb és legmélyebb tételei között szerepelnek a határeloszlás tételek.

Előként azt mondjuk, hogy

X n X

, amint

n

1 valószínűséggel (vagy majdnem biztosan), ha

A valószínűségszámításban a lehető legerősebb állítás, ha azt mondjuk, hogy valami 1 valószínűségű. Épp ezért a majdnem biztos konvergencia a legerősebb konvergencia fogalom. Néha a majdnem biztos helyett majdnem mindenütt kifejezést használnak.

A felszínes szemlélődőnek a valószínűségben kifejezés hasonló lehet az 1 valószínűséggel kifejezéshez. Azonban a valószínűségben való konvergencia sokkal gyengébb, mint a majdnem biztos konvergencia. Ezért az 1 valószínűséggel való konvergenciát szokás erős konvergenciának a valószínűségben való konvergenciát pedig gyenge konvergenciának nevezni. A következő feladatok a majdnem biztos konvergencia fogalmát járják körül. Jelölje

a pozitív racionális számok halmazát; nagyon fontos, hogy ez a halmaz megszámlálható.

Igazoljuk, hogy az alábbi események ekvivalensek:

$X n$ $nem$ konvergál $X$ -hez, amint $n$ .
Valamely $ε 0$ -ra $X n X ε$ végtelen sok $n$ -re.
Valamely $ε$ -ra $X n X ε$ végtelen sok $n$ -re.

Az előző feladat felhasználásával igazoljuk, hogy az alábbiak ekvivalensek:

$X n X amint n 1 .$
$X n X ε végtelen sok n -re 0$ tetszőleges $ε$ esetén. Segítség: használjuk a Boole egyenlőtlenséget!
$X n X ε végtelen sok n -re 0$ minden $ε 0$ esetén.
$X k X ε valamely k n -re 0 amint n$ minden $ε 0$ esetén.

Az előző feladat (c) része és az első Borel-Cantelli lemma következményeként kapjuk a majdnem biztos konvergencia következő kritériumát:

Igazoljuk, hogy ha $n 1 X n X ε$ minden $ε 0$ -ra, akkor $X n X$ amint $n$ 1 valószínűséggel.

A 25. feladat (c) részéből következik az alábbi állítás, amely a most tárgyalt témában az egyik legfontosabb eredményünk:

Igazoljuk, hogy ha $X n X$ amint $n$ 1 valószínűséggel, akkor $X n X$ amint $n$ valószínűségben.

Az előző állítás megfordítása nem igaz, erre egy példa a következő feladat.

Mint a 23. feladatban, tekintsünk végtelen sok számozott érmét. Minden $n$ -re az $n$ -edik érme feldobása után $1 n$ valószínűséggel mutat fejet. Az érmék mindegyikét feldobjuk, és a dobások eredményét feljegyezzük az $X 1 X 2$ sorozatba. Ezek nyilván független indikátor valószínűségi változók, amelyekre

X n 1 1 n, X n 0 1 1 n, n .

A második Borel-Cantelli lemma segítségével igazoljuk, hogy $X n 0 végtelen sok n -re 1$ , tehát 1 valószínűséggel végtelen sok írást dobunk.
A második Borel-Cantelli lemma segítségével igazoljuk, hogy $X n 1 végtelen sok n -re 1$ , tehát 1 valószínűséggel végtelen sok fejet dobunk.
Az (a) és a (b) pont segítségével lássuk be, hogy $X n nem konvergál, amint n 1$ .
Igazoljuk, hogy $X n 0 as n$ valószínűségben.

A 27. feladat állításának megfordítása tehát nem igaz, azonban a következő állítás (ami gyengébb, mint a megfordítás, de bizonyos értelemben mégis annak tekinthető) gyakran nagyon hasznos.

Igazoljuk, hogy ha $X n X$ amint $n$ valószínűségben, akkor létezik egy természetes számokból álló $n 1 n 2 n 3$ sorozat, hogy $X n k X$ amint $k$ 1 valószínűséggel.

Feltéve a valószínűségben való konvergenciát, igazoljuk, hogy minden $k$ -re létezik $n k$ , hogy $X n k X 1 k 1 k 2$ .
Az (a)-ban definiált sorozat elemei megadhatók úgy, hogy $n k n k 1$ teljesüljön minden $k$ -ra.
Az (a) és a (b) feladatokból lássuk be, hogy $k 1 X n k X ε$ minden $ε 0$ -ra.
A 26. feladatra hivatkozva lássuk be, hogy $X n k X$ amint $k$ 1 valószínűséggel.
A bizonyítás azért működött, mert $1 k 0$ amint $k$ és $k 1 1 k 2$ . Bármely sorozat, amely teljesíti ezt a két feltételt, használható.

Két további konvergencia típust fogunk még tárgyalni a későbbiekben, ezek a következők:

6. Konvergencia