A valószínűségszámítás az úgynevezett véletlen eseményekkel foglalkozik. Ezek olyan kísérletektől függő események, melyek kimenetelét nem tudjuk biztosan megjósolni, mielőtt a kísérletet elvégeznénk. A klasszikus vagy gyakoriságon alapuló valószínűségszámítás esetén mindig feltesszük, hogy a kísérletet tetszőleges sokszor meg tudjuk ismételni lényegében azonos körülmények között. Ez nagyon fontos feltevés, hisz a klasszikus valószínűségszámítás az kísérletek hosszú távú, aszimptotikus viselkedésével foglalkozik. Ezzel szemben az úgynevezett szubjektív valószínűségszámítás valamilyen értelemben azt méri, hogy mennyire hiszünk abban, hogy be fog következni egy adott esemény a kísérlet során. Ezért a korlátlanul sokszor való ismételhetőség feltétele nem olyan lényeges szempont. Amikor korrekt módon akarunk definiálni egy kísérletet, mindig pontosan meg kell mondanunk, hogy mit csinálunk, mit jegyzünk fel a kísérlet során, azaz, hogy mik a kísérlet lehetséges kimenetelei.
A paraméter kifejezést olyan mennyiségekre használjuk, melyek nem függnek a kísérlettől, azaz konstansok. Ezeket a kísérletek elvégzése előtt rögzítjük. A komolyabb kísérletek esetében általában több paraméter is megjelenik, amelyeket úgy szoktak beállítani, hogy a kísérlet a lehető legjobban közelítse a leírandó fizikai folyamatot.
A valószínűségszámítás és a statisztika bizonyos értelemben ellentétei egymásnak. Míg valószínűségszámítás esetén egy matematikailag pontosan definiált modellt akarunk leírni, azaz olyan számításokat végzünk, amelyek segítségével meg tudjuk jósolni, hogy a pontosan definiált kísérletünk során egyes események milyen valószínűséggel fognak bekövetkezni, addig a statisztikában egy nem teljesen ismert kísérlettel foglalkozunk. Gyakori eset például, hogy a kísérletben néhány paramétert nem ismerünk, és az a célunk, hogy sok adat alapján ezeket a paramétereket megbecsüljük.
Tegyük fel, hogy adott darab kísérlet: . Ekkor definiálhatunk egy új, úgynevezett összetett kísérletet, úgy, hogy az kísérletünket egymástól függetlenül sorban végrehajtjuk, először -et, aztán -t, így így tovább. Itt a független kifejezés intuitívan azt jelenti, hogy az egyes kísérletek kimenetelei nem befolyásolnak más kísérleteket. Természetesen később matematikailag precíz módon definiáljuk majd a függetlenség fogalmát.
Speciálisan gondolhatunk arra, hogy egy darab alapkísérletünk van. Ezt véges (vagy akár végtelen) sokszor, egymástól független módon megismételve egy összetett kísérletet kapunk. Valójában sok kísérlet összetett, és mint korábban említettük, a (klasszikus) valószínűségszámítás alapötlete pont a kísérletek egymástól független ismételgetése.
Tekintsük a legegyszerűbb esetet: a kísérletünknek két különböző kimenetele lehet. Ezt függetlenül ismételve kapjuk az úgynevezett Bernoulli kísérleteket (amelyet Jacob Bernoulli-ról neveztek el). Ez az egyik legegyszerűbb, és egyben legfontosabb modell a valószínűségszámításban. Kicsit általánosabban, tekinthetünk egy kísérletet különböző lehetséges kimenettel. Ennek egymástól független ismétléseit hívják multinomiális kísérleteknek.
Néha az is előfordul, hogy a kísérletünk jól szétválasztható lépésekben zajlik le, viszont ezek függenek egymástól, azaz egy adott lépésben bekövetkező eseményeket befolyásolnak a korábbi lépések kimenetelei.
A legtöbb statisztikai feladat esetén adott egy nagy halmaz (sokaság), amely érdekel minket, például emberek, alkatrészek, vagy kukoricaföldek. Általában az egyedek néhány mérhető tulajdonsága a fontos, például az emberek testmagassága, tömege, az alkatrészek élettartama, vagy a kukoricaföldek termésátlaga.
Jóllehet a halmaz minden elemének mérhető mennyisége érdekel minket, azonban az esetek többségében nem tudjuk az összes egyedet megmérni. Ilyenkor veszünk egy véletlen mintát, azaz kiválasztunk néhány egyedet véletlenszerűen, ezeknek megmérjük a releváns tulajdonságait, és ebből próbálunk meg az egész halmaz átlagos tulajdonságaira következtetni.
Alapvetően kétféle mintavételezési eljárás létezik. Az első a visszatevéses mintavétel. Ahogy a neve is mutatja, ebben az esetben a kiválasztott egyedet visszatesszük az eredeti halmazba, így előfordulhat, hogy egy egyedet többször is kiválasztunk. A második a visszatevés nélküli mintavétel, ezesetben egy egyedet legfeljebb egyszer választhatunk ki. A mintavételezési eljárásokat részletesen a Mintavételezési eljárások fejezetben tárgyaljuk.
A visszatevéses mintavételre úgy is gondolhatunk, mint egy összetett kísérletre, ami egyszerűen néhány darab független, adott halmazból való mintavételből áll. Fordítva, egy olyan összetett kísérlet, amely egy mintavételezés darab független megismétléséből áll, felfogható egy visszatevéses mintavételezési eljárásnak. Másrészt a visszatevés nélküli mintavételezés egy olyan kísérlet, amely egymástól függő lépésekből áll.
A valószínűségszámítás feladatait, módszereit, eredményeit gyakran különböző szerencsejátékokkal szemléltetjük: kártyával, dobókockával, érmedobással, urnákkal és golyókkal, stb. Ezek a példák nagyon hasznosak, hisz egyszerűek, és könnyen megérthető a véletlenség szerepe. Mindazonáltal nagyon szomorú lenne, ha a valószínűségszámítás módszerei csak szerencsejátékokra lennének alkalmazhatóak. Helyesen arra kell gondolnunk, hogy a szerencsejátékokból kölcsönzött példák csak leegyszerűsített változatai valódi, fizikai motivációjú, összetettebb feladatoknak.
Végezzünk érmedobás kísérletet, amelyben különböző érme feldobását szimuláljuk, és 1-et írunk, ha fejet, 0-t, ha írást dobtunk.
Az érmedobás kísérletben állítsuk be az paraméterértéket! Szimuláljunk 1000 kísérletet, és vizsgáljuk meg az eredményt!
Tekintsük a kockadobás kísérletet, amely különböző, oldalú "kocka" feldobását szimulálja. (A kockák lapjai 1-től -ig számozottak). esetén visszakapjuk a hagyományos kockát.
A kockadobás kísérletben állítsuk be az paraméterértéket! Szimuláljunk 1000 kísérletet, és vizsgáljuk meg az eredményt!
A kocka- és érmedobás kísérletében először feldobunk egy szabályos kockát, majd annyiszor dobunk fel egy pénzérmét, amennyit a kockánk mutat. Ez egy összetett kísérlet, melyben a lépések összefüggnek. Mik ezek a lépések?
Szimuláljunk 100 darab kocka- és érmedobás kísérletet, és vizsgáljuk meg a kísérletek kimenetelét!
Az érme- és kockadobás kísérletében először feldobunk egy érmét, majd ha ez fejet mutat, egy piros kockát, ha pedig írást mutat, egy kéket dobunk fel. Ez egy összetett kísérlet, melyben a lépések összefüggnek. Mik ezek a lépések?
Szimuláljunk 100 darab érme-, és kockadobás kísérletet, és vizsgáljuk meg a kísérletek kimenetelét!
Egy hagyományos francia kártyapakli az alábbi szorzathalmazzal modellezhető:
ahol az első koordináta a szám vagy figura (ász, 2-10, bubi, dáma, király), a második koordináta pedig a szín (treff, káró, kőr, pikk). Néha egy kártyát két egymás mellé írt szimbólum reprezentál, például .
Tekintsük a kártyakísérletet, ami nem más, mint kártya kiválasztása egy hagyományos kártyapakliból.
A kártyakísérletben állítsuk be az paraméterértéket! Szimuláljunk 1000 kísérletet, és vizsgáljuk meg az eredményt!
Az esetet nevezhetjük póker kísérletnek, az esetet pedig bridzs kísérletnek.
Tegyük fel, hogy van egy urnánk, benne különböző golyó, melyek meg vannak számozva 1-től -ig. A kísérletünk pedig az, hogy kiválasztunk golyót az urnából visszatevés nélkül, és feljegyezzük a golyók sorszámait.
Tekintsük az előző feladat urnamodelljét, most azonban legyen az urnában lévő golyók közül darab piros, a maradék darab pedig zöld. Ez által a modellünknek lesz egy új paramétere. Mi ez? Ez a kísérlet jól modellez egy kétpólusú populációból való mintavételezést
Az urna kísérletben állítsuk be az , és paraméterértékeket! Szimuláljunk 100 kísérletet, és vizsgáljuk meg a kimeneteleket!
Egy urnában kezdetben golyó van, ebből darab piros, és darab zöld. Kiválasztunk egy golyót, majd visszateszük az urnába darab, a kiválasztottal azonos színű golyót. Ezután ismételjük a fenti eljárást. Ezt nevezik Pólya urna modellnek, a magyar Pólya György tiszteletére.
A Buffon féle érmedobás kísérletben egy sugarú érmét dobunk fel egy olyan padló felett, melyet 1 egység oldalhosszúságú négyzet alakú csempékkel raktunk ki. Miután az érme földet ér, a középpontjának a csemperácsra vonatkozó koordinátáit feljegyezzük. A kísérlet Compte de Buffon-ról kapta a nevét.
A Buffon féle érmedobás kísérletében állítsuk be az paraméterértéket! Szimuláljunk 100 kísérletet, és vizsgáljuk meg a kimeneteleket!
A rendszerek megbízhatóságának elméletében általában egy elemből álló rendszert tekintenek, melynek minden eleme működik, vagy elromlott. Az egyes elemek állapotát nem mindig ismerjük, innen származik a véletlenség. Az egész rendszerre is értelmezhető, hogy működik, vagy elromlott. A soros kapcsolású rendszerek esetén például az egész rendszer pontosan akkor működik, ha minden komponense működik. A párhuzamos kapcsolású rendszerek ezzel ellentétben pontosan akkor működnek, ha legalább az egyik elemük működik. Általánosabban, az -ből elemű rendszerek pontosan akkor működnek, ha elemük működik.
Tekintsünk egy -ből elemű rendszert!
A fent definiált megbízhatóságelméleti modell egy statikus modell. Természetesen kiterjeszthető dinamikus modellé például úgy, hogy feltételezzük, hogy kezdetben minden elem üzemel, majd egy véletlen időpontban elromlik. Ekkor egy véletlen időpontban elromolhat a rendszer, és ez a véletlen időpont jelen esetben függ az alkatrészek meghibásodási idejétől, és a rendszer szerkezetétől is.
Általában az ivaros szaporodás esetén az utód génállománya a szülők génállományának véletlen keveréke. Tehát egy gyerek születése felfogható egy véletlen kísérletnek, ahol a kimenetelek lehetnek szemszín, hajszín, vagy egyéb testi tulajdonságok. Ezt a véletlen öröklődési folyamatot természetesen nagy érdeklődés követi.
Tekintsünk egy rendkívül egyszerű modellt: az öröklött tulajdonság csak kétféle lehet, például egy borsó hüvelye vagy sárga, vagy zöld. Egy ilyen növénynek két génje van, ami ezt a tulajdonságot kódolja (mindkét szülőtől egy), így a lehetséges géntípusok a következők:
A és a típusú egyedeket homozygótának, a típusú egyedeket heterozygótának hívják. Tipikusan az egyik típusú gén domináns, míg a másik recesszív. Ha például a zöld állapot a domináns a hüvely színére nézve, akkor a és a génállományú borsók zöld hüvelytermést hoznak, míg a génállományú borsók sárgát. A szülőktől az utódok mindig véletlenszerűen kapják a géneket, így minden új növény egy véletlen kísérlet, ahol a kimenetek a lehetséges termésszínek.
A borsóhüvely színe az egyik legelső olyan genetikai tulajdonság volt, melyet tudományosan vizsgáltak. Gregor Mendel, akit a modern genetika atyjának tekintenek, úttörő volt az ilyen kutatások területén, a borsóhüvely színén kívül a virág színét (sárga vagy lila), a szár hosszát (rövid vagy hosszú), és a mag jellegét (sima felületű, vagy ráncos) is vizsgálta.
Egy tipikus nemtől függő öröklődő emberi rendellenesség az X kromoszóma zavara (ez egy a két olyan kromoszóma közül, amely meghatározza az emberek nemét). Jelölje a normál, pedig a rendellenességet okozó hibás gént. A nőknek két darab X kromoszómájuk van, a típusú pedig tipikusan recesszív. Tehát egy génállományú nő teljesen egészséges, míg egy génállományú nő egészséges ugyan, de hordozza a betegséget, hisz átadhatja a gyerekeinek a hibás gént, végül a génállományú nő beteg. A férfiaknak egy X kromoszómájuk van (a másik nemi kromoszóma, az úgynevezett Y kromoszóma ebben a rendelleneségben nem játszik szerepet). Így egy génállományú férfi egészséges, egy génállományú férfi beteg. Az előzőekben leírt betegségre példa a dikromácia, vagy színtévesztés, illetve a hemofília, vagy vérzékenység. A szülőktől az utódok mindig véletlenszerűen kapják a géneket, így minden újszülött egy véletlen kísérletnek tekinthető, ahol a kimenet lehet rendellenes, vagy egészséges.
Sok fontos fizikai jelenséget véletlen időpontokkal
írhatunk le. Gyakran ezeket az időpontokat érkezési időpontoknak, vagy felújítási időpontoknak nevezik. Néhány példa ilyen jelenségre:
Kétféleképp is végezhetünk kísérletet: feljegyezhetjük egy adott időintervallumba eső pontok számát, vagy feljegyezhetjük az egymást követő pontok között eltelt időt.
Más esetekben véletlen térbeli pontfolyamatról
beszélhetünk. Ilyenek például:
Ha ilyen esetben formalizálni akarunk egy kísérletet, akkor feljegyezzük egy adott térrészbe eső véletlen pontok számát.
1879-ben Albert Michelson kísérleti úton próbálta megmérni a fény sebességét egy interferométerrel. A kapott sebesség adathalmaz 100 kísérleti eredményt tartalmaz. Vizsgáljuk meg az adathalmazt, és magyarázzuk meg, hogy általában miért ingadoznak a mérési eredmények!
1998-ban két egyetemi hallgató az Alabamai egyetemről a következő kísérletet végezte: vásároltak egy zacskó M&Ms cukorkát, és megszámolták, hány piros, zöld, kék, narancs, és citromsárga színű cukorka van benne, majd megmérték a zacskó tömegét. Vizsgáljuk meg az M&M adathalmazt, és magyarázzuk meg, hogy általában miért ingadoznak a mérési eredmények!
1999-ben egyetemi kutató a Belmont egyetemről a következő kísérletet végezte: Tennessee állam középső részén megfogtak egy kabócát, megmérték a testtömegét (grammban), a szárny szélességét és hosszát, a testhosszt (milliméterben), megvizsgálták még a kabóca nemét, és az alfaj típusát.A kabóca adathalmaz 104 kísérlet eredményét tartalmazza. Vizsgáljuk meg az adathalmazt, és magyarázzuk meg, hogy általában miért ingadoznak a mérési eredmények!
1761 június 6-án James Short 53 alkalommal megmérte a Nap Földhöz viszonyított, Vénusz okozta parallaktikus szögelmozdulását. Vizsgáljuk meg Short adathalmazát, és magyarázzuk meg, hogy általában miért ingadoznak a mérési eredmények!
1954-ben két kísérletet végeztek annak eldöntésére, hogy mennyire hatékony a Jonas Salk által kifejlesztett paralízis-védőoltás. Mindkét kísérletben beoltottak egy csoport gyereket, ezt nevezik kezelt csoportnak, miközben megfigyeltek egy úgynevezett kontrollcsoportot is, azaz egy be nem oltott gyerekekből álló csoport. Mindkét csoportban feljegyezték a paralízises megbetegedések számát. Vizsgáljuk meg a paralízis-oltás adathalmazát, és vázoljuk a mögötte rejlő véletlen kísérletet!
1969 és 1972 között minden évben kisorsolták az Egyesült Államokban, hogy kit hívjanak be katonai szolgálatra. A sorsolás lényegében egy golyók és urna modell volt, és azért vált híressé, mert sokak szerint a sorsolás nem volt eléggé véletlenszerű... Vizsgáljuk meg a Vietnam sorsolás adathalmazát, és gondolkozzunk el azon, hogyan lehetne eldönteni, mennyire volt véletlen a sorsolás.
Egyesek vélekedhetnek úgy, hogy a fenti példák valójában deterministikusak. Például egy érmedobásnál ha ismerjük a kezdeti feltételeket (feldobás helye, sebessége, kezdeti szögsebesség, stb.), a levegőben az érmére ható erőket (gravitáció, légellenállás), valamint a pénzérme fizikai tulajdonságait (alakját, tömegeloszlását, tömegközéppontját, stb.), akkor a fizika törvényei alapján kiszámolhatjuk, hogy melyik oldalára esik majd le. Ez elvileg igaz, gyakorlatilag azonban a számolás kivitelezhetetlen. Ugyanis az érme-, kockadobás, és sok más bonyolultabb rendszer kaotikus, azaz a végeredmény a kezdeti érték pici módosítása esetén is drasztikusan változhat. Ilyen esetekben sosem ismerjük olyan pontossággal a kezdeti feltételeket, hogy meg tudnánk jósolni a kísérlet végkimenetelét.
Az érmedobás kísérletét vizsgáljuk meg egy kicsit részletesebben. Egyszerűsítsük a feladatot, még így igaz lesz, hogy a kísérlet lényegében véletlen. A következő elemzés Joseph Keller: The Probability of Heads
című cikkéből származik. Itt a szerző az alábbi alapfeltevésekkel él:
Természetesen a fenti feltevések nagy része nem teljesül a valódi érmedobás esetén. Legyen , ahol a gravitációs gyorsulás (megfelelő mértékegységben mérve). Vegyük észre, hogy a idő mértéke nem függ attól, hogy hogyan mérjük a távolságot. Lényegében azt méri, mennyi ideig repül az érme felfelé.
Keller igazolta, hogy a pár azon paramétertartományait, ahol az érme fejre, vagy írásra érkezik, az
görbék határolják, ahol a levegőben történő teljes megfordulások száma. Néhány görbe látható az alábbi ábrán. A legnagyobb, bal alsó tartomány azon paraméterpárokhoz tartozik, amikor az érme egyszer sem fordul meg, és így természetesen fejjel felfelé érkezik, hisz így dobtuk fel. A következő tartomány azon paraméterértékeket adja, amikor az érme pontosan egyszer fordul meg, és persze a végén írást mutat. És így tovább, minden szomszédos tartománypár esetén az érmedobás eredménye különböző.
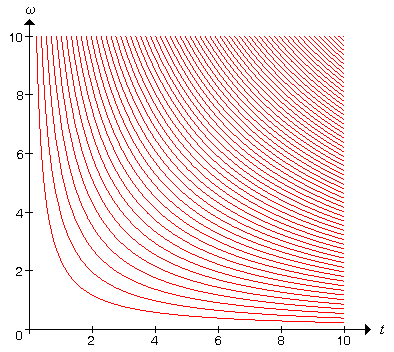
A lényeges eredmény az, hogy akár nem túl nagy és értékekre már nagyon közel esnek egymáshoz a határoló görbék, tehát a kezdeti értékekben történő apró változtatás már befolyásolhatja a kísérlet eredményét. Keller megjegyzi a cikkében, hogy a valószínűségszámítással és statisztikával foglalkozó neves kutató, Persi Diaconis megmérte, hogy egy valós érmedobás esetén a tipikus paraméterértékek másodperc, és radián másodpercenként. Ezen paraméterek esetén alkalommal pördül meg az érme. Ez a paraméterpár már nem szerepel az ábránkon, itt a határoló görbék már rettentő közel vannak egymáshoz.