Tegyük fel, hogy adott egy véletlen kísérlet egy eseménytérrel. Ekkor szemléletesen egy esemény valószínűsége azt méri, hogy mennyire várható, hogy a kísérlet során az adott esemény bekövetkezik.
A matematikailag precíz definíció a következő: a véletlen kísérletünkhöz tartozó valószínűségi mérték (vagy eloszlás) egy, az eseményeken értelmezett valós értékű függvény, amely eleget tesz az alábbi axiómáknak:
A 3. axiómát nevezik megszámlálható additivitásnak, ami azt jelenti, hogy véges, vagy megszámlálhatóan végtelen sok diszjunkt halmaz uniójának valószínűsége épp a külön-külön vett valószínűségek összege. A fenti axiómákat Kolmogorov axiómáknak nevezik Andrei Kolmogorov tiszteletére.
Az 1. és 2. axióma csak egy skálázást ad: minden esemény valószínűsége 0 és 1 közötti szám (lehetett volna másképp is definiálni, de így volt a legtermészetesebb). A 3. axióma viszont nagyon fontos. Érezhetjük, hogy a megszámlálható additivitási tulajdonságot nemcsak a valószínűségektől várhatjuk el, hanem más mértékektől is, azaz más olyan függvényektől is, amelyek bizonyos halmazok méretét
adják meg. Ilyenek például a következők:
A fenti esetek mindegyikében megszámlálható sok diszjunkt halmaz uniójának mérete a halmazok méretének összegével egyenlő. Általános mértékelméletről bővebben a Mértékelmélet részben olvashatunk.
Másfelől a nem megszámlálható additivitást (azaz a 3. axióma kiterjesztését tetszőleges, tehát nem feltétlenül megszámlálható indexhalmazra) természetes, hogy nem tesszük fel a valószínűségi (és semmilyen más) mértékekre. Hiszen például egy pozitív hosszúságú valós intervallum felírható nem megszámlálható (pontosan kontinuum sok) pont uniójaként, amelyek hossza természetesen nulla.
Tehát már definiáltuk a véletlen kísérletek leírásához szükséges 3 alapvető objektumot:
A fenti három objektumot együttesen valószínűségi mezőnek nevezzük.
Szemléletesen egy esemény valószínűsége azt kell, hogy mérje, hogy ha nagyon sokszor végrehajtjuk a kísérletet, mi a relatív gyakorisága az esemény bekövetkezésének (Richard Von Mises ezt tekintette a valószínűség definíciójának). Pontosabban tegyük fel, hogy egy kísérletet meg tudunk ismételni korlátlan sokszor (ezáltal egy új, összetett kísérletet kapunk). Az eredeti kísérlet egy eseményére jelölje azon kísérletek számát az első kísérlet között, amelyek során bekövetkezett (ezt nevezzük az esemény gyakoriságának). Vegyük észre, hogy ez egy, az összetett kísérlettől függő valószínűségi változó. Továbbá
az esemény relatív gyakorisága az első kísérlet során (ami szintén egy, az összetett kísérlettől függő valószínűségi változó). Ha a megfelelő valószínűségi mértéket választottuk, akkor természetes elvárás, hogy a relatív gyakoriságnak valamilyen értelemben a valószínűséghez kell konvergálnia:
Ennek a pontos megfogalmazását nevezik a nagy számok törvényének, ami az egyik legfontosabb tétel a valószínűségszámításban. Hangsúlyozzuk, hogy az axiómákat kielégítő valószínűségi mérték rengeteg létezhet, azonban csak a valódi fogja teljesíteni a nagy számok törvényét.
Tehát ha ismerünk egy kísérlet eredményét tartalmazó adathalmazt, akkor a megfigyelt relatív gyakorisággal közelíthetjük a valódi valószínűséget. Ezt a közelítést úgy nevezik, hogy az esemény tapasztalati-, vagy empirikus valószínűsége.
Igazoljuk, hogy eleget tesz a valószínűségi mértékek axiómáinak (ahol természetesen adott egy kísérleti eredményt tartalmazó adathalmaz)!
Tegyük fel, hogy egy értékű valószínűségi változó.
Igazoljuk, hogy egy valószínűségi mértéket definiál -n!
Segítség: Emlékezzünk vissza arra a tényre, hogy az őskép képzés felcserélhető a halmazműveletekkel!
Az előző feladatban definiált valószínűségi mértéket az változó valószínűségi eloszlásának nevezzük. Tehát minden, a kísérletünktől függő valószínűségi változó segítségével definiálhatunk egy új valószínűségi mezőt:
Minden kísérlet kimenetele is tekinthető valószínűségi változónak. Azaz ha speciálisan az identitás függvény -en, akkor egy valószínűségi változó, és
Tehát minden valószínűségi mértékre gondolhatunk úgy, mint egy valószínűségi változó eloszlására.
Hogyan konstruálhatunk valószínűségi mértékeket? Ahogy az előbb már megjegyeztük, más mértékek is léteznek, melyek bizonyos halmazok méretét
mérik valamilyen értelemben; sokszor ezekből könnyen előállíthatunk valószínűségi mértéket. Egy (nemnegatív)
mérték egy
halmazon egy valós értékű függvény, melynek értelmezési tartománya események egy
családja, és amely eleget tesz a fenti 1. és 3. axiómának. Általában
lehet végtelen is valamilyen
halmazra. Ha viszont
pozitív és véges, akkor
könnyen átskálázható egy valószínűségi mértékké.
Igazoljuk, hogy ha egy mérték -en, és , akkor az alább definiált egy valószínűségi mérték -en:
A 3. feladatban látott esetekben -et normáló konstansnak nevezik. A következő két pontban nagyon fontos speciális eseteket tekintünk.
Legyen egy véges, nem üres halmaz. Nyilván a jellel jelölt számláló mérték egy véges mérték -en:
Az ehhez tartozó valószínűségi mértéket -en értelmezett diszkrét egyenletes eloszlásnak nevezik:
Megszámlálható halmazok esetén általánosabb konstrukcióval még több valószínűségi mértéket előállíthatunk:
Tegyük fel, hogy egy nem üres, megszámlálható halmaz, és egy -en értelmezett nemnegatív valós értékű függvény. Igazoljuk, hogy az alábbi függvény mérték -en:
Tehát, ha , akkor a 3. feladat értelmében egy valószínűségi mérték. Az ilyen eloszlásokat nevezzük diszkrét eloszlásoknak. A Diszkrét eloszlásokkal részletesen az Eloszlások című fejezetben foglalkozunk.
Az előző feladat jelölései mellett igazoljuk, hogy ha véges, és konstans függvény, akkor a kapott valószínűségi mérték épp a diszkrét egyenletes eloszlás -en!
Legyen a standard -dimenziós mérték a mérték -en, amelyre
Ezt a mértéket Lebesgue mértéknek nevezik Henri Lebesgue tiszteletére. Igazából a fenti integrál egy kicsit általánosabb, mint az alap analízisből ismert Riemann integrál, de az esetek túlnyomó többségében ennek pontos ismeretére nem lesz szükségünk. Azaz feltehetjük, hogy az halmaz elég szép, így az integrál létezik (erről a témáról kicsit bővebben lesz szó a Mérhetőségről szóló fejezetben). Természetesen ha , akkor a fenti integrál többváltozós, , és . A megszámlálható additivitási tulajdonság az integrálok megfelelő tulajdonságából következik. Közismert analízisbeli tény, hogy
Ha olyan halmaz, hogy , akkor
egy valószínűségi mérték -en a 3. feladat értelmében. Ezt az eloszlást nevezik -en értelmezett folytonos egyenletes eloszlásnak.
Az előző konstrukció általánosításával sok más eloszlást is definiálhatunk. Tegyük fel, hogy egy -en értelmezett nemnegatív valós értékű függvény, és legyen
Ekkor egy mérték -en. Így ha , akkor a 3. feladat értelmében egy valószínűségi mérték. Az ilyen eloszlásokat folytonos (vagy abszolút folytonos) eloszlásoknak nevezzük. Ezekkel részletesen az Eloszlások fejezet folytonos eloszlások című részében foglalkozunk.
A matematika sok más ágával ellentéteben a valószínűségszámításban az alacsony () dimenziós esetek semmilyen megkülönböztetett jelentőséggel nem bírnak. Például a kabóca kísérlet adathalmazában néhány megmért jellemző a testtömeg, a testhossz, a szárnyhossz, és a szárnyszélesség. Az ezen jellemzőket leíró valószínűségi modell egy részhalmazán értelmezett eloszlás lenne.
Tegyük fel, hogy adott egy véletlen kísérlet az eseménytéren, a hozzá tartozó valószínűségi mértékkel. A következő feladatokban és eseményeket jelölnek. A feladatok megoldásánál a valószínűségi mértékek axiómáit használjuk!
Igazoljuk, hogy . Ezt a szabályt nevezhetjük komplementer szabálynak.
Segítség: és diszjunktak, és az uniójuk .
Igazoljuk, hogy .
Segítség: Alkalmazzuk a komplementer szabályt -re!
Igazoljuk, hogy . Ezt a szabályt nevezhetjük a különbségképzésre vonatkozó szabálynak
Segítség: és diszjunktak, és az uniójuk .
Igazoljuk, hogy ha , akkor .
Segítség: Alkalmazzuk a különbségképzésre vonatkozó szabályt, és hogy
Igazoljuk, hogy ha , akkor .
Tehát egy növekvő függvény (ahol az események közti részben rendezés a tartalmazás szerinti, rendezése pedig a szokásos). Speciálisan, minden eseményre.
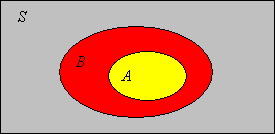
Tegyük fel, hogy . Igazoljuk, hogy
Legyen események egy megszámlálható családja. Igazoljuk a Boole egyenlőtlenséget (amelyet George Boole-ról neveztek el):
Szemléletesen a Boole egyenlőtlenség azért igaz, mert a bal oldalon szereplő unió némely részét a jobb oldalon "többször mértük".
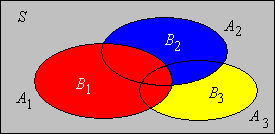
Legyen események megszámlálható osztálya, hogy , amint . A Boole egyenlőtlenség segítségével igazoljuk, hogy
Az olyan eseményt, melyre , lehetetlen, vagy nullmértékű eseménynek nevezzük. Az előző eredményünk szerint tehát nullmértékű események megszámlálható uniója is nullmértékű.
Legyen események egy megszámlálható családja. Igazoljuk a Bonferroni egyenlőtlenséget (amely Carlo Bonferroni-ról kapta a nevét):
Segítség: Alkalmazzuk a Boole egyenlőtlenséget a halmazrendszerre!
Legyen események megszámlálható osztálya, hogy , amint . A Bonferroni egyenlőtlenség segítségével igazoljuk, hogy
Az olyan eseményt, amelyre , majdnem biztos eseménynek nevezzük. Az előző feladatunk szerint tehát majdnem biztos események megszámlálható metszete is majdnem biztos.
Legyenek és a kísérletünktől függő események. Igazoljuk az alábbiakat:
Tegyük fel, hogy egy megszámlálható partíciója az eseménytérnek (más szóval teljes esemény rendszer). Igazoljuk, hogy tetszőleges eseményre
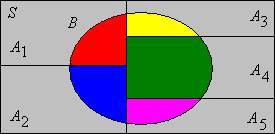
Természetesen ez az eredmény akkor hasznos, ha a benne szereplő metszetek valószínűségeit ismerjük. Partíciók gyakran valószínűségi változó kapcsán merülnek fel. Tegyük fel például, hogy egy valószínűségi változó, mely a megszámlálható halmazban veszi fel az értékeit, pedig egy tetszőleges esemény. Ekkor
Természetesen ebben a formulában a vessző szerepe ugyanaz, mint az előző formulában a metszet jel szerepe.
A szitaformula események uniójának valószínűségét néhány esemény metszetének valószínűsége segítségével fejezi ki.
Igazoljuk, hogy tetszőleges és eseményekkel.

Igazoljuk, hogy tetszőleges , és eseményekkel.
Segítség: Használjuk háromszor a két eseményre vonatkozó szitaformulát!
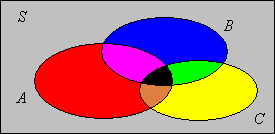
Az előzőkét feladat általánosítható tetszőleges eseményre, ezt az általánosítást nevezzük szitaformulának.
Legyen egy esemény minden -re, ahol . Igazoljuk, hogy
Segítség: használjunk -re vonatkozó indukciót!
Az általános Bonferroni egyenlőtlenség azt állítja, hogy ha a 20. feladatban szereplő összeg jobb oldalán csak -ig összegzünk (), akkor ez az összeg egy felső becslés az unió valószínűségére, ha páratlan (azaz az utolsó összeadandó pozitív előjelű), és alsó becslés, ha páros (azaz az utolsó összeadandó negatív előjelű).
A 6-20. feladatok megoldásai triviálisan általánosíthatók tetszőeges véges mértékre. Az egyetlen különbség, hogy az 1 konstanst -re kell cserélni. Speciálisan, a szitaformula a kombinatorikában legalább olyan fontos, mint a valószínűségszámításban.
Szemléletesen az ekvivalens események vagy valószínűségi változók olyanok, amelyek valószínűségszámítási szempontból megkülönböztethetetlenek. Ebben a részben ezt a fogalmat definiáljuk matematikailag korrekt módon.
Az és eseményekre azt mondjuk, hogy ekvivalensek, ha a szimmetrikus differenciájuk valószínűsége 0:
Igazoljuk, hogy az ekvivalencia valóban ekvivalencia reláció egy véletlen kísérlet eseményein! Azaz az eseményeket particionálhatjuk olyan módon, hogy az egy partícióba eső események kölcsönösen ekvivalensek.
Igazoljuk, hogy ekvivalens események valószínűsége megegyezik: ha és ekvivalensek, akkor
Az előző állítás megfordítása természetesen nem igaz. Tekintsünk például egy érmedobás kísérletet, és igazoljuk, hogy az a két esemény, hogy az érme fejet, illetve hogy írást mutat, azonos valószínűségű, de nem ekvivalens!
A null- és a majdnem biztos események ekvivalencia osztályokat alkotnak.
Legyenek most és egy kísérlettől függő valószínűségi változók, melyek helyettesítési értéküket a halmazban veszik fel. Ekkor és ekvivalensek, ha
Igazoljuk, hogy a fenti ekvivalencia valóban a értékű valószínűségi változók ekvivalencia relációja! Azaz a valószínűségi változókat particionálhatjuk olyan módon, hogy az egy partícióba eső valószínűségi változók kölcsönösen ekvivalensek.
Tegyük fel, hogy és ekvivalens, értékű valószínűségi változók! Igazoljuk, hogy minden részhalmazra az és az események ekvivalensek! Lássuk be, hogy és azonos eloszlású!
Legyenek és egy véletlen kísérlettől függő események. Igazoljuk, hogy és pontosan akkor ekvivalensek, ha az és az indikátor valószínűségi változók ekvivalensek!
Tegyük fel, hogy és ekvivalens, értékű valószínűségi változók, továbbá egy -ből -ba képező függvény. Igazoljuk, hogy és ekvivalensek!
Tegyük fel, hogy és olyan események, hogy , , . Fejezzük ki szavakkal, hogyan függnek a következő események a kísérlettől, és számítsuk ki a valószínűségüket:
Tegyük fel, hogy , és olyan események, amelyekre , , , , , , . Fejezzük ki halmazműveletekkel a következő eseményeket, és határozzuk meg a valószínűségüket:
Legyenek és olyan események, amelyekre , , és . Határozzuk meg a következő események valószínűségeit:
Legyenek és olyan események, amelyekre , , és . Határozzuk meg a következő események valószínűségeit:
Az érmedobás kísérletben feldobunk különböző érmét, és a dobott értékeket feljegyezzük az vektorba (1-et írunk, ha fejet dobtunk, 0-t, ha írást). Jelölje a fejek számát.
Az előző feladat kísérlete a Bernoulli kísérletek speciális esete (amelyeket Jacob Bernoulli-ról neveztek el). A fejek számát jelölő binomiális eloszlású.
Tekintsük az érmedobás kísérletet 3 igazságos érmével. Legyen az az esemény, hogy az első érme fejet mutat, pedig az az esemény, hogy pontosan 2 fejet dobtunk. Határozzuk meg a következő valószínűségeket:
Az Érmedobás kísérletben válasszunk 3 érmét. Szimuláljunk 1000 kísérletet (frissítsük az ábrát minden kísérlet után), és számítsuk ki az előző feladatban szereplő események relatív gyakoriságát!
A kockadobás kísérletben feldobunk különböző, oldalú kockát (ezek oldalai 1-től -ig be vannak számozva), és a dobott értékeket lejegyezzük az vektorba. Ez egy általános példa az multinomiális kísérletre, és a véges populációból vett visszatevéses mintavételezésre. A speciális esetet nevezzük hagyományos kockadobásnak.
Feljegyeztük két hagyományos, igazságos kockadobás eredményét az vektorba. Jelölje azt az eseményt, hogy az első kockadobás eredménye kisebb mint 3, pedig azt az eseményt, hogy a dobott számok összege 6.
A Kockadobás kísérletben legyen a kockák száma . Szimuláljunk 100 kísérletet, és határozzuk meg az előző feladatban szereplő események relatív gyakoriságát!
Feldobtunk 2 szabályos, hagyományos kockát, és a dobott számokat feljegyeztük az vektorba. Legyen a dobott számok összege, a kisebbik dobott szám, pedig a nagyobbik dobott szám!
Tekintsük a következő kísérletet: egy pár hagyományos kockát addig dobunk fel, amíg először azt nem látjuk, hogy a dobott számok összege 5 vagy 7. Jelölje azt az eseményt, hogy az utolsó dobásnál a dobott számok összege 5 (és nem 7). Ilyen típusú kísérletek fordulnak elő a craps nevű játékban.
Egy hagyományos francia kártyapakli az alábbi szorzathalmazzal modellezhető:
ahol az első koordináta a szám vagy figura (ász, 2-10, bubi, dáma, király), a második koordináta pedig a szín (treff, káró, kőr, pikk). Néha egy kártyát két egymás mellé írt szimbólum reprezentál, például .
A kártyakísérletben visszatevés nélkül kiválasztunk kártyát egy hagyományos, jól megkevert kártyapakliból, és a kártyákat feljegyezzük az vektorba, ahol az -edik kiválasztott kártya. Jelölje a kiválasztott kártyák halmazát (rendezés nélkül).
Az speciális eset a póker kísérlet, az speciális eset pedig a bridzs kísérlet. A póker kísérletről részletesebben a Szerencsejátékok fejezetben olvashatunk.
Tekintsünk egy kártya kísérletet kártyával. -re jelölje azt az eseményt, hogy az -edik kártya kőr.
A kártya kísérletben legyen . Szimuláljunk 100 kísérletet, és határozzuk meg az előző feladatban szereplő események relatív gyakoriságát!
Határozzuk meg a póker kísérletben az alábbi események valószínűségét:
Szimuláljunk 1000 póker kísérlet (frissítsük az ábrát minden tizedik után), és határozzuk meg az előző feladatokban szereplő események relatív gyakoriságát!
Határozzuk meg annak a valószínűségét, hogy a bridzs kísérletben nem húztunk sem tízest, sem bubit, sem dámát, sem királyt, sem ászt! Az ilyen leosztást szokás Yarborough-nak nevezni Yarborough őrgróf tiszteletére.
Határozzuk meg annak a valószínűségét, hogy a bridzs kísérletben kiválasztott lapok között
A szitaformula segítségével határozzuk meg az alábbi események valószínűségeit:
A Buffon féle érmedobás kísérletben egy sugarú érmét véletlenszerűen feldobunk egy olyan padló felett, melyet 1 egység oldalhosszúságú négyzet alakú csempékkel raktunk ki. Miután az érme földet ér, a középpontjának koordinátáit -vel jelöljük, ahol az origó annak a csempének a középpontja, amelyikre az érmeközéppont esik, a koordinátatengelyek pedig párhuzamosak a csemperács éleivel. Legyen az az esemény, hogy az érme csak egy csempéhez ér hozzá, és jelölje az érme középpont origótól való távolságát.
A Buffon féle érmedobás kísérlet szimulációjában állítsuk be az paraméterértéket! Szimuláljunk 100 kísérletet, és határozzuk meg az előző feladatban szereplő események relatív gyakoriságát!
Tegyük fel, hogy van egy urnánk, benne különböző golyó, melyek meg vannak számozva 1-től -ig. A kísérletünk pedig az, hogy kiválasztunk golyót az urnából visszatevés nélkül, és feljegyezzük a golyók sorszámait az vektorba. Legyen a kiválasztott golyók (rendezetlen) halmaza. Ez a modell lényegében egy véges populációból való visszatevés nélküli mintavételezés.
Tekintsük az előző feladat urnamodelljét, most azonban legyen az urnában lévő golyók közül darab piros, a maradék darab pedig zöld. Ismét egy elemű mintát veszünk a golyókból. Jelölje a kiválasztott piros golyók számát! Ez a kísérlet lényegében egy kétpólusú populációból való visszatevés nélküli mintavételezés. Ekkor az valószínűségi változó hipergeometriai eloszlású. Határozzuk meg lehetséges értékeit, és igazoljuk, hogy
Legyen az urnánkban 30 golyó, melyek közül 10 piros és 20 zöld. Tegyük fel, hogy 5 golyót választottunk ki véletlenszerűen. Számítsuk ki az előző feladatban szereplő valószínűségek értékeit ebben a konkrét esetben!
Az urna és golyók kísérlet szimulációjában állítsuk be az előző feladat paramétereit (30 golyó, ebből 10 piros, 20 zöld, és ötöt választunk ki). Szimuláljunk 1000 kísérletet, és hasonlítsuk össze az relatív gyakoriságokat az előző feladatban meghatározott pontos értékekkel!
Egy urnában 12 golyó van: 5 piros, 4 zöld és 3 kék. Kiválasztunk 3 golyót véletlenszerűen, visszatevés nélkül.
Oldjuk meg az előző feladatot azzal a módosítással, hogy most visszatevéssel választjuk ki a golyókat!
Tekintsünk egy rendkívül egyszerű modellt: egy öröklött tulajdonság csak kétféle lehet, például egy borsó hüvelye vagy sárga, vagy zöld. Egy ilyen növénynek két génje van, ami ezt a tulajdonságot kódolja (mindkét szülőtől egy), így a lehetséges géntípusok a következők:
A és a típusú egyedeket homozygótának, a típusú egyedeket heterozygótának hívják. Általában az egyik típusú gén domináns, míg a másik recesszív. Ha például a zöld állapot a domináns a hüvely színére nézve, akkor a és a génállományú borsók zöld hüvelytermést hoznak, míg a génállományú borsók sárgát. A szülőktől az utódok mindig véletlenszerűen kapják a géneket, így minden új növény egy véletlen kísérlet, ahol a kimenetek a lehetséges termésszínek. A borsók hüvelyszínének ilyen vizsgálata Gregor Mendel, a modern genetika úttörője nevéhez fűződik.
Legyen az az esemény, hogy az utód genotipusa , az az esemény, hogy a genotipus , pedig az az esemény, hogy a genotipus . Határozzuk meg a , és valószínűségeket az alábbi esetek mindegyikében:
Egy tipikus nemtől függő öröklődő emberi rendellenesség az X kromoszóma zavara (ez egy a két olyan kromoszóma közül, amely meghatározza az emberek nemét). Jelölje a normál, pedig a rendellenességet okozó hibás gént. A nőknek két darab X kromoszómájuk van, a típusú pedig tipikusan recesszív. Tehát egy génállományú nő teljesen egészséges, míg egy génállományú nő egészséges ugyan, de hordozza a betegséget, hisz átadhatja a gyerekeinek a hibás gént, végül a génállományú nő beteg. A férfiaknak egy X kromoszómájuk van (a másik nemi kromoszóma, az úgynevezett Y kromoszóma ebben a rendelleneségben nem játszik szerepet). Így egy génállományú férfi egészséges, egy génállományú férfi beteg. Az előzőekben leírt betegségre példa a dikromácia, vagy színtévesztés, illetve a hemofília, vagy vérzékenység. A következő feladatban kiszámolhatjuk, hogy mikor milyen valószínűséggel öröklődik az ilyen genetikai rendellenesség.
Legyen az az esemény, hogy egy fiúgyermek beteg, az az esemény, hogy egy lánygyermek hordozza a betegséget, pedig az az esemény, hogy egy lánygyermek beteg. Határozzuk meg a , és a valószínűségeket az alábbi esetek mindegyikében:
Az előző feladatból levonhatjuk azt a következtetést, hogy egy lánygyermek csak akkor lehet beteg, ha az anya legalább hordozó, és az apa beteg. Egy nagy populációban ez igen ritka esemény, ezért a nemtől függő öröklődő rendellenességek sokkal kevésbé gyakoriak a nőknél, mint a férfiaknál. Röviden úgy is mondhatjuk, hogy a nőket védi az a tény, hogy két X kromoszómájuk van.
Jelölje annak az időintervallumnak a hosszát (milliszekundumokban mérve), amely egy adott radioaktív anyag által történő két kibocsátás között eltelik, és tegyük fel, hogy exponenciális eloszlású, azaz:
Jelölje a radioaktív anyag által egy milliszekundum alatt kibocsátott részecskék számát, és tegyük fel, hogy Poisson eloszlású, azaz:
Egy titkárnő darab levelet ír, és meg is címez darab borítékot a megfelelő címzetteknek (ez darab különböző ember), de a leveleket a borítékokba véletlenszerűen rakja bele. Jelölje azt az eseményt, hogy legalább egy levelet a megfelelő borítékba rakott.
Az alábbi lépések és a szitaformula segítségével igazoljuk, hogy
Az előző feladat eredményének segítségével igazoljuk, hogy
Határozzuk meg pontos értékét az és az esetekben! Hasonlítsuk össze az eredményeket a limeszben kapott valószínűséggel!
A párosítás kísérlet részletes tárgyalása a véges mintavételezési eljárásokról szóló fejezetben található.
Az M&M adathalmazban legyen az az esemény, hogy a zacskóban van legalább 10 piros cukorka, az az esemény, hogy a zacskóban van legalább 57 cukorka, és az az esemény, hogy a zacskó van legalább 50 gramm tömegű. Határozzuk meg a következő események relatív gyakoriságát:
A kabóca adathalmazban legyen az az esemény, hogy a kabóca tömege legalább 0,2 gramm, az az esemény, hogy a kabóca nőstény, és az az esemény, hogy a kabóca alfaja tredecula. Határozzuk meg a következő események relatív gyakoriságát: