]> A gamma eloszlás
  1. Virtual Laboratories
  2. 4. Nevezetes eloszlások
  3. 1
  4. 2
  5. 3
  6. 4
  7. 5
  8. 6
  9. 7
  10. 8
  11. 9
  12. 10
  13. 11
  14. 12
  15. 13
  16. 14
  17. 15

3. A gamma eloszlás

Ebben a fejezetben egy fontos eloszláscsaláddal, a gamma eloszlások családjával foglalkozunk. Ebbe az eloszláscsaládba tartozik az érkezési idők eloszlása a Poisson folyamatokban, és a statisztikában is fontos khí-négyzet eloszlás.

A gamma függvény

A gamma függvény (melyet először Leonhard Euler definiált) definíciója a következő:

k s 0 s k 1 s ,  k 0 .

Igazoljuk, hogy a gamma függvény jól definiált, azaz a definiáló integrál konvergens minden k 0 esetén!

A gamma függvény grafikonját a 0 5 intervallumon az alábbi ábrán láthatjuk:

The gamma function

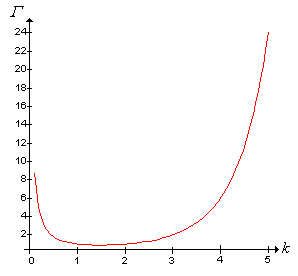
Parciális integrálással igazoljuk, hogy k 1 k k tetszőleges k 0 esetén.

A 2. feladatot felhasználva igazoljuk, hogy k k 1 ha k pozitív egész.

A standard normális sűrűségfüggvény felhasználásával igazoljuk, hogy 12 .

Az egyik leghíresebb aszimptotikus összefüggés a következő, úgynevezett Stirling formula (mely James Stirling-ről kapta a nevét):

x 1 x x 2 x  amint   x .

Tehát speciálisan

n n n 2 n  amint   n .

Az alap gamma eloszlás

Igazoljuk, hogy a következő függvény egy valószínűségi sűrűségfüggvény minden k 0 esetén

f x 1 k x k 1 x ,  x 0 .

Ha az X valószínűségi változó sűrűségfüggvénye a fenti függvény, akkor azt mondjuk, hogy X k -ad rendű gamma eloszlású. A következő feladat megoldásával láthatjuk, hogy milyen sokféle lehet a sűrűségfüggvény alakja a rend függvényében. Ezért szokás az előző k paramétert alakparaméternek is nevezik.

Vázoljuk a gamma sűrűségfüggvény grafikonját az alábbi esetekben:

  1. 0 k 1 ,
  2. k 1 ,
  3. k 1 . Ebben az esetben igazoljuk azt is, hogy a módusz az x k 1 helyen vétetik fel.

A valószínűségi változók kísérletében válasszuk a gamma eloszlást! Változtassuk az alakparaméter értékét, és figyeljük meg a sűrűségfüggvény alakját! Néhány k értékre szimuláljunk 1000 kísérletet (frissítsük az ábrát minden tizedik után), és figyeljük meg, hogyan konvergál az empirikus sűrűségfüggvény a valódi sűrűségfüggvényhez!

Egy bizonyos alkatrész élettartama (100 órákban mérve) gamma eloszlású k 3 alakparaméterrel. Mennyi annak a valószínűsége, hogy az alkatrész 300 óránál is tovább üzemel?

A gamma eloszlás eloszlásfüggvényét és kvantilis függvényét nem lehet zárt elemi képlettel felírni, viszont közelíthetjük őket a kvantilis applet, illetve egyéb matematikai vagy statisztikai szoftverek segítségével.

A kvantilis applet segítségével határozzuk meg a gamma eloszlás mediánját, alsó és felső kvartilisét és az interkvartilis terjedelmét az alábbi esetek mindegyikében:

  1. k 1 ,
  2. k 2 ,
  3. k 3 .

A következő feladatban a gamma eloszlás várható értékét és szórásnégyzetét határozzuk meg.

Legyen X k -rendű gamma eloszlású. Igazoljuk, hogy

  1. X k ,
  2. X k .

Általánosabban, a momentumokat könnyen kifejezhetjük a gamma függvény segítségével:

Legyen X gamma eloszlású k alakparaméterrel. Igazoljuk, hogy

  1. X n n k k amint n 0 ,
  2. X n n k n n 1 n k 1 ha n pozitív egész.

A következő feladatban a momentum generáló függvényt határozzuk meg.

Legyen X gamma eloszlású k alakparaméterrel. Igazoljuk, hogy

t X 1 1 t k ,  t 1 .

A valószínűségi változók kísérletében válasszuk a gamma eloszlást. Változtassuk az alakparamétert, és figyeljük meg a várható értéket és szórást jelölő csúszka helyét és méretét. Néhány k értékre szimuláljunk 1000 kísérletet (frissítsük az ábrát minden tizedik után), és figyeljük meg, hogyan konvergálnak az empirikus momentumok az eloszlás valódi momentumaihoz!

Egy bizonyos virág szirmának hossza (cm-ben mérve) gamma eloszlású k 4 alakparaméterrel. Határozzuk meg a virágszirom hosszának várható értékét és szórását!

Az általános Gamma eloszlás

Az általános gamma eloszlás annyiban tér el az eddig tárgyalttól, hogy még bevezethetünk egy skála-paramétert. Tehát ha Z alap gamma eloszlású k alakparaméterrel, akkor b 0 esetén X b Z gamma eloszlású k alakparaméterrel és b skála-paraméterrel. Az alakparaméter reciprokát - különösen a Poisson folyamatok tárgyalása esetén - szokás rátának nevezni. Speciálisan a k 1 és b paraméterű gamma eloszlást nevezik b skála-paraméterű (vagy r 1 b rátaparaméterű) exponenciális eloszlásnak.

Az alap gamma eloszlásnál látott állítások megfelelőit az általános esetben könnyen beláthatjuk a skálatranszformációra vonatkozó általános szabályok alapján.

Legyen X gamma eloszlású k alak- és b skála-paraméterrel. Igazoljuk, hogy X sűrűségfüggvénye az alábbi függvény:

f x 1 k b k x k 1 x b ,  x 0 .

Ahogy azt már tárgyaltuk, a skála-paraméter bevezetése nem változtatja meg a sűrűségfüggvény alakját, csak skálázza azt. Tehát a sűrűségfüggvény lehetséges alakjai ugyanazok, mint amiket már a 6. feladatban láttunk.

Legyen X gamma eloszlású k alak- és b skála-paraméterrel. Igazoljuk, hogy ha k 1 akkor az eloszlás módusza x k 1 b .

Legyen X gamma eloszlású k alak- és b skála-paraméterrel. Igazoljuk, hogy

  1. X k b ,
  2. X k b 2 .

Legyen X gamma eloszlású k alak- és b skála-paraméterrel. Igazoljuk, hogy

  1. X n b n n k k ahol n 0 ,
  2. X n b n n k b n n n 1 n k 1 ha n pozitív egész.

Legyen X gamma eloszlású k alak-, és b skála-paraméterrel. Igazoljuk, hogy X momentum generáló függvénye

t X 1 1 b t k ,  t 1 b .

A valószínűségi változók kísérletében válasszuk a gamma eloszlást. Változtassuk a paraméterek értékét, és figyeljük meg a sűrűségfüggvényt, valamint a várható értéket és a szórást jelölő csúszka helyét és méretét. Néhány paraméterértékre szimuláljunk 1000 kísérletet (frissítsük az ábrát minden tizedik után), és figyeljük meg, hogyan konvergál az empirikus sűrűség és az empirikus momentumok az eloszlás valódi sűrűségfüggvényéhez és momentumaihoz!

Egy bizonyos alkatrész élettartama (órákban kifejezve) gamma eloszlású k 4 alak- és b 100 skála-paraméterrel.

  1. Mennyi annak a valószínűsége, hogy az alkatrész több mint 300 óráig fog üzemelni?
  2. Határozzuk meg az élettartam várható értékét és szórását!

Transzformációk

Az első transzformáció, melyet tekintünk, alátámasztja a skála-paraméter elnevezés helyességét.

Legyen X gamma eloszlású k alak-, és b skála-paraméterrel. Igazoljuk, hogy ha c 0 , akkor c X gamma eloszlású k alak- és b c skála-paraméterrel!

A következő feladatban egy fontos állítást látunk be, miszerint a rögzített skála-paraméterű gamma eloszlások családja zárt a konvolúcióra nézve (azaz független gamma eloszlású változók összege is gamma eloszlású).

Legyen X i gamma eloszlású k i alakparaméterrel, és b skála-paraméterrel, ahol i 1 2 . Tegyük fel továbbá, hogy X 1 és X 2 függetlenek. Igazoljuk, hogy X 1 X 2 gamma eloszlású k 1 k 2 alak- és b skála-paraméterrel! Segítség: használjunk momentum generáló függvényeket!

Legyen X gamma eloszlású k alak- és b skála-paraméterrel. Igazoljuk, hogy ezek az eloszlások egy kétparaméteres exponenciális eloszláscsaládot alkotnak, ahol a természetes paraméterek k 1 1 b , a természetes statisztikák pedig X X .

Normális approximáció

A 23. feladat értelmében ha Y k gamma eloszlású k alak- és rögzített b skála-paraméterrel, akkor

Y k i 1 k X i ,

ahol X 1 X 2 független valószínűségi változók sorozata, melyek mindegyike b paraméterű exponenciális eloszlású. A centrális határeloszlás-tétel szerint viszont ha k nagy, akkor a gamma eloszlás approximálható k b várható értékű és k b 2 szórásnégyzetű normális eloszlással. Pontosabban a tétel értelmében az alábbi standardizált változó eloszlása konvergál a standard normális eloszláshoz amint k :

Z k Y k k b k b .

A valószínűségi változók kísérletében válasszuk a gamma eloszlást. Változtassuk a paraméterek értékét, és figyeljük meg a sűrűségfüggvény alakját! Néhány paraméterértékre szimuláljunk 1000 kísérletet (frissítsük az ábrát minden tizedik után), és figyeljük meg, hogyan konvergál az empirikus sűrűségfüggvény az eloszlás valódi sűrűségfüggvényéhez!

Tegyük fel, hogy Y gamma eloszlású k 10 és b 2 paraméterekkel. Az alábbi értékeket határozzuk meg a kvantilis applet segítségével, majd közelítsük őket a normális approximációval! Vessük össze a kapott eredményeket!

  1. 18 Y 25 ,
  2. Y 0,8-kvantilise.

  1. Virtual Laboratories
  2. 4. Nevezetes eloszlások
  3. 1
  4. 2
  5. 3
  6. 4
  7. 5
  8. 6
  9. 7
  10. 8
  11. 9
  12. 10
  13. 11
  14. 12
  15. 13
  16. 14
  17. 15