The Zeta Distribution

The zeta distribution is used to model the size or ranks of certain types of objects randomly chosen from certain types of populations. Typical examples include the frequency of occurrence of a word randomly chosen from a text, or the population rank of a city randomly chosen from a country. The zeta distribution is also known as the Zipf distribution, in honor of the American linguist George Zipf.

The Zeta Function

The Riemann zeta function

, named after Bernhard Riemann, is defined as follows:

(You might recall from calculus that the series in the zeta function converges for

a 1

and diverges for

a 1

. A graph of the zeta function on the interval

110

is given below:

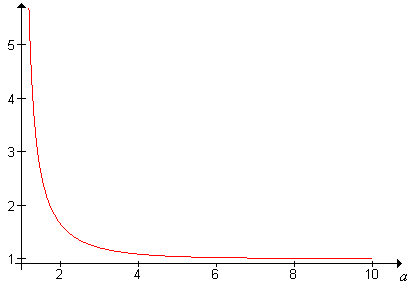
Try to verify the main properties of the graph analytically. In particular, show that

is decreasing.
is concave upward.
$a 1$ as $a$
$a$ as $a 1$

The zeta function is transcendental, and most of its values must be approximated. However,

a

can be given explicitly for even integer values of

a

; in particular,

226

and

4490

The Probability Density Function

Show that the function $f$ given below is probability density function for any $a 1$ .

f n 1 a n a, n

The discrete distribution defined by the density function in Exercise 2 is called the zeta distribution with parameter

a

. In an algebraic sense, the zeta distribution is a discrete version of the Pareto distribution.

Let $X$ denote the frequency of occurrence of a word chosen at random from a certain text, and suppose that $X$ has the zeta distribution with parameter $a 2$ . Find $X 4$ .

Suppose that $X$ has the zeta distribution with parameter $a$ . Show that the distribution is a one-parameter exponential family with natural parameter $a$ and natural statistic $X$ .

Moments

The moments of the zeta distribution can be expressed easily in terms of the zeta function.

Suppose that $X$ has the zeta distribution with parameter $a$ and that $k 0$ . Show that

X k a k 1 a k a a k 1

In particular, show that

$X a 1 a$ if $a 2$ .
$X a 2 a a 1 a 2$ if $a 3$ .

Let $X$ denote the frequency of occurrence of a word chosen at random from a certain text, and suppose that $X$ has the zeta distribution with parameter $a 4$ . Approximate each of the following:

$X$ .
$X$ .

10. The Zeta Distribution

The Zeta Function

The Probability Density Function

Moments