Mint az alap mintavételi modellben, tételezzük fel, hogy véletlenszerűen kiválasztunk számot visszatevéssel a populációból. Így az eredményvektor
ahol az -edik kiválasztott. Emlékeztetünk arra, hogy az alapmodell feltevése az, hogy egyenletes eloszlású az
mintatéren.Ebben a részben a mintából hiányzó populációs értékek száma és a mintában lévő (különböző) populációs értékeknek a száma érdekel minket. A valószínűségek kiszámítását, amelyek kapcsolatban állnak ezekkel a valószínűségi változókkal, általában úgy nevezik, hogy születésnapi problémák. Gyakran, a mintavételi kísérletet úgy értelmezzük, mint golyónak rekeszbe (dobozba) való szétosztását; az . golyó dobozának a száma. Ebben az értelmezésben minket az üres dobozok száma és a foglalt dobozok száma érdrkel.
-re jelölje azon alkalmaknak a számát, amikor előfordul a mintában:
Mutassuk meg, hogy polinomiális eloszlású és paraméterekkel:
Most definiáljuk a fő (minket érdelkő) valószínűségi változókat: a mintában a hiányzó populációs értékek számát:
és a mintában előforduló (különböző) populációs értékeknek a számát:
Nyilvánvaló, hogy így miután egy változónak ismert az eloszlása és momentuma, könnyen megtalálhatjuk a másik változóra is ezeket. Először a születésnap probléma legegyszerűbb esetét oldjuk meg.
Az az esemény, hogy a mintában létezik legalább egy duplikátum, a következőképpen írható fel:
Az egyszerű születésnap probléma abból áll, hogy kiszámítsuk ennek az eseménynek a valószínűségét. Például, tételezzük fel, hogy véletlenszerűen kiválasztunk személyt és feljegyezzük születésnapjaikat. Ha a szökőévet figyelmen kívül hagyjuk és feltesszük, hogy a születésnapok egyenletes eloszlásúak egész éven át, akkor alkalmazzuk az egyszerű mintavételi modellünket értékkel. Ezzel a beállítással a születésnap probléma az, hogy kiszámítsuk annak valószínűségét, hogy legalább két személynek ugyanakkor van a születésnapja (Ez a speciális eset a probléma "névadója").
A születésnap probléma megoldása a kombinatorikus valószínűség egy egyszerű feladata.
Felhasználva a kombinatorika szorzási szabályát mutassuk meg, hogy
Útmutatás: Az komplementer esemény akkor és csak akkor következik be, ha az eredményvektor, egy a -ből vett méretű permutációvektort alkot.
A tényre, hogy esetén a valószínűség 1, néha úgy hivatkozunk, mint a galambdúc elvre: ha több, mint galambot helyezünk el oduba, akkor legalább egy oduba 2, vagy több galamb kerül.
Jelölje a komplementer esemény valószínűségét, , hogy a mintaváltozók különböznek. Bizonyítsuk be a következő rekurzív összefüggést két módon: először a 2. gyakorlat eredményéből kiindulva, majd ezután felhasználva a feltételes valószínűségről tanultakat.
Legyen (a standard születésnapi probléma). Ellenőrizzük a következő születésnappal kapcsolatos valószínűségeket:
Ábrázoljuk az előző gyakorlatban lévő értékeket, mint függvényét. Amikor a görbe sima (a forma kedvéért), az alábbi görbére fog hasonlítani.
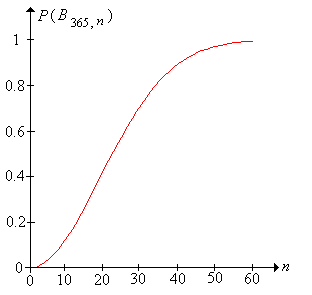
A születésnap kísérletben legyen és válasszuk a indikátor változót -nek. -ra végezzük el a kísérletet 1000-szer és számítsuk ki annak az eseménynek a relatív gyakorisását, hogy a minta tartalmaz duplikációt. Hasonlítsuk össze a relatív gyakoriságokat az előző gyakorlatban kiszámított valószínűségekkel.
A könnyű megoldás ellenére, a születésnap probléma híres probléma, mert numerikusan, a valószínűségek egy kicsit meglepőek. Megjegyezzük, hogy éppen 60 személy esetén az esemény majdnem biztos. Matematikailag a születésnap-valószínűség gyors növekedése (amint növekszik) annak a ténynek köszönhető, hogy sokkal gyorsabban nő, mint .
Négy szabályos dobókockát feldobunk. Adjuk meg annak valószínűségét, hogy a dobott számok különbözőek.
A születésnap kísérletben, legyen és válasszuk indikátorváltozónak -t. Változtassuk értékét a görgetősávval és figyeljük meg a grafikonon, hogyan változnak a valószínűségek. Most -re végezzük el a kísérletet 1000-szer, 10-esével frissítve a gyakoriságokat. Figyeljük meg az esemény relatív gyakoriságának nyilvánvaló konvergenciáját a megfelelő valószínűséghez.
Véletlenszerűen választunk 5 személyt.
A születésnap kísérletben, legyen és válasszuk indikátorváltozónak -t. Változtassuk -et a görgetősávval és figyeljük meg a grafikonon, hogyan változnak a valószínűségek. Most -re végezzük el a kísérletet 1000-szer, 10-esével frissítve a gyakoriságokat. Figyeljük meg az esemény relatív gyakoriságának nyilvánvaló konvergenciáját a megfelelő valószínűséghez..
Egy gyorsétterem 10 különböző játékból ajándékoz egyet gyermekadag vásárlásakor. Egy család 5 gyermeknek 5 gyermakadagot vásárol. Adjuk meg annak valószínűségét, hogy a kapott 5 játék különböző!
A születésnap kísérletben, legyen és válasszuk indikátorváltozónak -t. Változtassuk -et a görgetősávval és figyeljük meg a grafikonon, hogyan változnak a valószínűségek. Most -re végezzük el a kísérletet 1000-szer, 10-esével frissítve a gyakoriságokat. Figyeljük meg az esemény relatív gyakoriságának nyilvánvaló konvergenciáját a megfelelő valószínűséghez.
Térjünk vissza az általánosabb problémához: megadni a különböző mintaértékek számának eloszlását és a kimaradt mintaértékek számának eloszlását.
-re vizsgáljuk azt az eseményt, hogy nem fordul elő a mintában: . Most legyen kikötéssel. Felhasználva a kombinatorika szorzási szabályát, könnyű megszámlálni azon mintáknak a számát, amelyek nem tartalmazzák minden elemét:
Mutassuk meg, hogy
Most a kombinatorika tartalmazás-kizárás szabályát használva ki tudjuk számolni azon mintáknak a számát, amikor legalább egy populációs érték hiányzik:
Mutassuk meg, hogy
Először is láthatjuk, hogy egyszerű megszámolni azon minták számát, amelyek nem tartalmazzák az összes populációs értéket:
Mutassuk meg, hogy
Most használhatunk egy kétlépéses eljárást, amivel az összes mintát, generálhatjuk, amiből pontosan darab populációs érték marad ki:
Így alkalmazhatjuk a kombinatorika szorzási szabályát, hogy megszámoljuk azon minták számát, melyekből darab populációs érték hiányzik.
Mutassuk meg, hogy
Végül, mivel eloszlása az mintatéren egyenletes, meg tudjuk adni a kizárt értékek számának sűrűségfüggvényét:
Mutassuk meg, hogy
Könnyen meg tudjuk adni a mintában lévő különböző értékek számának sűrűségfüggvényét:
Mutassuk meg, hogy
A születésnap kísérletben, válasszuk meg a különböző mintaértékek számát. Változtassuk a paramétereket és figyeljük meg a sűrűségfüggvény helyét és alakját. A paraméterek kiválasztott értékeire végezzük el a kísérletet 1000-szer, 10-esével frissítve és figyeljük meg a relatív gyakoriság függvény nyilvánvaló konvergenciáját az elméleti sűrűségfüggvényhez.
A kizárt értékek számának eloszlását megkaphatjuk egy rekurziós okoskodással is.
Legyen esetén. Felhasználva valószínűségszámítási érveket mutassuk meg, hogy
Most megkeressük a várható értékeket és a szórásnégyzeteket. A kizárt értékek száma és a különböző értékek száma számláló változók és ezért felírhatók, mint indikátorváltozók összegei. Mint már láttuk sok modellben, ez a reprezentáció gyakran a legjobb a momentumok számítására.
Legyen . Így ha bekövetkezik, ami azt jelenti, hogy nincs a mintában és egyébként. Megjegyezzük, hogy a mintában levő populációs értékek száma felírható, mint indikátor változók összege:
Mutassuk meg, hogy
Felhasználva a 22. gyakorlat eredményét mutassuk meg, hogy
Felhasználva a 22. gyakorlat eredményét, mutassuk meg, hogy
Felhasználva a 24. gyakorlat eredményét és a szórásnégyet elemi tulajdonságait mutassuk meg, hogy
A születésnap kísérletben válasszuk meg a különböző mintaértékek számát. Változtassuk a paramétereket és figyeljük meg az átlag/standard eloszlás ábrájának helyét és méretét. A paraméterek kiválasztott értékeire végezzük el a kísérletet 1000-szer 10-esével frissítve és figyeljük meg a minta átlag és szórásnégyzet nyilvánvaló konvergenciáját a várható értékhez és elméleti szórásnégyzethez.
Tételezzük fel, hogy véletlenszerűen kiválasztunk 30 személyt.
A születésnap kísérletben legyen és . Végezzük el a kísérletet 1000-szer 10-esével frissítve és számítsuk ki az utolsó gyakorlat (d) részében szereplő esemény relatív gyakoriságát.
Tételezzük fel, hogy 10 szabályos dobókockát dobunk fel.
A születésnap kísérletben legyen és . Végezzük el a kísérletet 1000-szer 10-esével frissítve és számítsuk ki az utolsó gyakorlat (d) részében szereplő esemény relatív gyakoriságát.
Egy gyorsétteremben 10 különböző játék valamelyikét adják mindegyik gyerek menü vásárlásakor. Egy család 15 gyermekadagot vásárol.
A születésnap kísérletben legyen és . Végezzük el a kísérletet 1000-szer 10-esével frissítve és számítsuk ki az utolsó gyakorlat (d) részében szereplő esemény relatív gyakoriságát.
A hazug hallgatók problémája. Tételezzük fel, hogy 3 hallgató, akik együtt utaznak, hiányoznak egy matematikavizsgáról. Elhatározzák, hogy azt hazudják az oktatónak, hogy az autó kereke defektes lett. Az oktató elkülönítette a három hallgatót egymástól és mindegyiküket egyenként megkérdezte, hogy mi okozta a kerék defektjét. A hallgatók, akik ezt nem látták előre, véletlenszerűen és egymástól függetlenül válaszoltak.
A kacsavadász probléma. Tételezzük fel, hogy van 5 kacsavadász, mindegyikük kifogástalan lövő. Egy 10 kacsából álló csapat repül felettük, és mindegyik kacsavadász véletlenszerűen kiválaszt magának egy kacsát és lő.