]> Rendstatisztikák
  1. Virtuális laboratóriumok
  2. 11. Véges mintavételi modellek
  3. 1
  4. 2
  5. 3
  6. 4
  7. 5
  8. 6
  9. 7
  10. 8
  11. 9

4. Rendstatisztikák

Alapelmélet

Valószínűségi változók

Tételezzük fel, hogy populációnk 1-től m -ig van számozva úgy, hogy D 1 2 m . Például, a populáció állhat gyárilag előállított tételekből és ezeket megjelölhetjük a megfelelő sorozatszámokkal. Mint az alap mintavételi modellben válasszunk véletlenszerűen visszatevés nélkül n objektumot D -ből:

X X 1 X 2 X n

ahol X i D az i -edik választott objektum. Emlékeztetünk arra, hogy X egyenletes eloszlású a D -ből választott n elemű permutációk halmaza fölött. Emlékeztetünk arra, hogy

W X 1 X 2 X n

egy rendezetlen minta, amely egyenletes eloszlású a kombinációk n elemű D -ből vett halmaza fölött.

i 1 2 n esetén legyen

X n i i  -edik legkisebb eleme a  X 1 X 2 X n halmaznak.

Az X n i valószínűségi változó az X minta esetén, mint az i -edik rendstatisztika ismert. Megjegyezzük, hogy a szélső (extrémális) statisztikák:

X n 1 X 1 X 2 X n X n n X 1 X 2 X n

Mutassuk meg, hogy X n i értékeit az i i 1 m n 1 halmazból veszi.

A rendstatisztikák vektorát jelöljük

Y X n 1 X n 2 X n n -nal.

Megjegyezzük, hogy Y értékeit az L x 1 x 2 x n D n x 1 x 2 x n halmazból veszi.

Végezzük el a rendstatisztika kísérletet. Figyeljük meg, hogy meg tudjuk változtatni a populáció méretet, m -et és a mintaméretet, n -et. A rendstatisztikákat mindegyik frissítéskor jegyezzük fel (regisztráljuk).

Eloszlások

Mutassuk meg, hogy L -nek m n eleme van és hogy Y egyenletes eloszlású az L halmazon. Útmutatás: Y x 1 x 2 x n akkor és csak akkor, ha W x 1 x 2 x n és akkor és csak akkor, ha X az x 1 x 2 x n n permutációjának egyike.

Felhasználva egy kombinatorikai összefüggést, mutassuk meg, hogy X n i sűrűségfüggvénye

X n i k k 1 i 1 m k n i m n ,  k i i 1 m n i

A rendstatisztika kísérletben változtassuk a paramétereket és figyeljük meg a sűrűségfüggvény helyét és alakját. A paraméterek kiválasztott értékeire végezzük el a kísérletet 1000-szer, 10-esével frissítve. Figyeljük meg a relatív gyakoriság függvény jól látható konvergenciáját a sűrűségfüggvényhez.

Momentumok

A 4. gyakorlatban a sűrűségfüggvényt megkaphatjuk a binomiális együtthatók egy érdekes azonosságának a felhasználásával. Ez az azonosság használható X n i várható értékének és szórásnégyzetének meghatározásához is.

Mutassuk meg, hogy 1 i n m esetén

k i m n i k 1 i 1 m k n i m n

Mutassuk meg, hogy

X n i i m 1 n 1
  1. Induljunk ki a várható érték definíciójából.
  2. Mutassuk meg, hogy k k 1 i 1 i k i
  3. Használjuk fel a 6. gyakorlatban szereplő azonosságot m -et m 1 -gyel, n -et n 1 -gyel és i -t i 1 -gyel helyettesítve.
  4. Egyszerűsítsük az eredményt.

Felhasználva a 6. gyakorlat eredményét mutassuk meg, hogy

X n i i n i 1 m 1 m n n 1 2 n 2

A rend statisztika kísérletben változtassuk a paramétereket és figyeljük meg a várható érték/statndard szórás grafikonjának helyét és méretét. A paraméterek kiválasztott értékeire végezzük el a kísérletet 1000-szer, 10-esével frissítve. Figyeljük meg a minta átlagának és standardizát szórásának jól látható konvergenciáját az eloszlás várható értékéhez és standard szórásához.

m rendstatisztikákon alapuló becslései

Felhasználva a 7. gyakorlat eredményeit mutassuk meg, hogy i 1 2 n esetén a következő statisztika m -nek torzítatlan becslése:

U n i n 1 i X n i 1

Mivel U n i torzítatlan, szórásnégyzete az átlagos négyzetes hiba, a becslés minőségének a mértéke.

Felhasználva a 8. gyakorlat eredményét, mutassuk meg, hogy

U n i m 1 m n n i 1 i n 2

Mutassuk meg, hogy fix m -re és n -re U n i csökken, mint i függvénye. Így, a becslések javíthatók, ha i -t növeljük; speciálisan U n n a legjobb és U n 1 a legrosszabb.

Ellenőrizzük a következő arányt, ami U n j -nek U n i -re vonatkozó relatív hatékonysága néven ismert:

U n i U n j j n i 1 i n j 1 .

Megjegyezzük, hogy a relatív hatékonyság csak a i és j sorrendjétől függ, valamint az n mintamérettől, de nem függ az m populációs mérettől. Speciálisan U n n U n 1 -re vonatkozó relatív hatékonysága n 2 .

Általában, reméljük, hogy a becslés javítható (átlagos négyzetes hiba tekintetében), ha a minta n méretét növeljük (több információ esetén jobb lesz a becslésünk). Ez az általános összefüggés konzisztencia néven ismert.

Ellenőrizzük a következő eredményt. U n n 0-hoz tart, miközben n növekszik 1-től m -ig, és így U n n konzisztens:

U n n m 1 m n n n 2

Mutassuk meg, hogy fix i esetén U n i először nő, majd csökken 0-ig, ha n növekszik i -től m -ig. Így U n i inkonzisztens (nem konzisztens).

A következő ábra U n 1 függvényt mutatja, n függvényeként m 100 esetén.

The variance of Un,1 as a function of n

m becslésén alapuló mintaátlagról

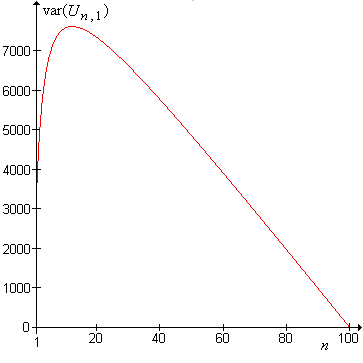
Ebben a részfejezetben az m paraméter egy másik egy másik becslésének levezetését adjuk meg, ami az M n 1 n i 1 n X n mintaváltozó átlagán ( röviden mintaátlagon) alapul és összehasonlítjuk ezt a becslést a változó maximumán alapuló becsléssel ( legnagyobb rendstatisztika).

Mutassuk meg, hogy M n m 1 2 .

  1. Emlékeztetünk arra, hogy X i egyenletes eloszlású a D hamazon minden i -re.
  2. Mutassuk meg, vagy emlékezzünk vissza arra, hogy X i m 1 2 .

Látható, hogy V n 2 M n 1 m -nek torzítatlan becslése. Továbbá úgy tűnik, hogy látszólag V n több információt használ a mintából (mivel több mintaváltozót foglal magába) mint U n n . Valóban jobbat? Jöjjünk rá, hogy szükséges kiszámolnunk a becslés szórásnégyzetét (amely mivel torzítatlan, az átlagos négyzetes hibával egyezik meg). Ez a számítás egy kicsit komplikált, mivel a mintaváltozók függetlenek. Ki fogjuk számolni az összeg szórásnégyzetét, mint a a páronként vett kovarianciák összegét.

Mutassuk meg, hogy X i X j m 1 12 i j -re.

  1. Először elevenítsük fel, hogy adott X i k , X j egyenletes eloszlású a D k halmazon.
  2. Most mutassuk meg, hogy X j X i k m m 1 2 m 1 k m 1 .
  3. Használjunk egy feltételes érvelést annak megmutatásásra, hogy X i X j m 1 3 m 2 12 .
  4. Végül használjuk fel a (c)-ben, a 16(b)-ben kapott eredményeket és a kovariancia statndard formuláját.

Elevenítsük fel, vagy mutassuk meg, hogy X i m 2 1 12 .

Mutassuk meg, hogy M n m 1 m n 12 n .

  1. A páronkénti kovarianciák összegében n tag van, a 18. gyakorlatban adott értékkel.
  2. A páronkénti kovarianciák összegében n 2 n tag van, a 17. gyakorlatban adott értékkel.

Végül mutassuk meg, hogy V n m 1 m n 3 n .

A 20. gyakorlatban szereplő szórásnégyzet csökken n függvényeként, s így V n becslése konzisztens. Számítsuk ki a várható értéken alapuló becsléshez a maximum szerinti becslés relatív hatékonyságát.

Mutassuk meg, hogy V n U n n n 2 3 .

Ilymódon, mégegyszer láthatjuk, hogy a maximumon alapuló becslés jobb.

Visszatevéses mintavétel

Ha a mintavétel visszatevéses, akkor az X X 1 X 2 X n minta független és azonos eloszlású valószínűségi változóknak egy sorozata. Az ilyen mintákból vett rendstatisztikákat a Véletlen minták fejezetében tanulmányozzuk.

Példák és alkalmazások

Tételezzük fel, hogy egy lottójátékban az 1-től 25-ig számozott sorsjegyek egy tálban vannak elhelyezve. Öt sorsjegyet választunk véletlenszerűen, visszatevés nélkül.

  1. Adjuk meg X 5 3 sűrűségfüggvényét!
  2. Adjuk meg az X 5 3 várható értéket!
  3. Adjuk meg X 5 3 szórásnégyzetét!

A német tank probléma

Az U n n becslést a szövetségesek felhasználták a II.világháborúban a német tankok m számának a becslésére. A német tankoknak volt egy sorozatszámuk és az elfoglalt német tankok valamint hiteles feljegyzések alkották a mintaadatokat. A statisztikai becslésekről kiderült, hogy pontosabbak, mint a hírszerzői becslések. Néhány adatot mellékelünk az alábbi táblázatban.

Német tankadatok
Dátum Statistikai becslés Hírszerzői becslés Német adatrekordok
1940. június 169 1000 122
1941. június 244 1550 271
1942. augusztus 327 1550 342

Az eset egy nyilvánvaló tanulsága, hogy ne tegyünk sorozatszámot a fegyverünkre!

Tételezzük fel, hogy egy háborúban 5 ellenséges tankot zsákmányoltunk. Ezek sorozatszáma 51, 3, 27, 82, 65. Számítsuk ki m becslését, a tankok teljes számát, felhasználva a fentebb tárgyalt becslések mindegyikét.

A rendstatisztikai kísérletben legyen m 100 , n 10 . Végezzük el a kísérletet 50-szer, minden kísérlet után frissítve. Mindegyik kísérlet esetén számítsuk ki m rendstatisztikáin alapuló becslését. Mindegyik becslésre számítsuk ki a hibanégyzetek átlagának négyzetgyökét az 50 kísérlet után. Ezen empirikus hibabecslés alapján rangsoroljuk m becsléseit a becslés pontossága (minősége) szerint!

Tételezzük fel, hogy egy bizonyos háborúban 10 tankot zsákmányoltunk. Ezek sorszáma 304, 125, 417, 226, 192, 340, 468, 499, 87, 352. Adjuk meg az összes tankok számának m becslését, felhasználva a maximumon és az összegen alapuló becslést.

  1. Virtuális laboratóriumok
  2. 11. Véges mintavételi modellek
  3. 1
  4. 2
  5. 3
  6. 4
  7. 5
  8. 6
  9. 7
  10. 8
  11. 9