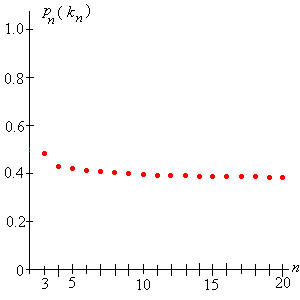
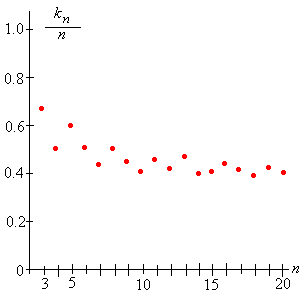
Ebben a részben tanulmányozni fogunk egy szép problémát, ami többféle néven is ismert, mint pédául titkárnő probléma vagy házasodási probléma. Egyszerű megállapítani, hogy a problémát nem nehéz megoldani, de a megoldás érdekes és egy kicsit meglepő. A probléma egy kellemes bevezetést szolgáltat a statisztikai döntések általános területére.
Mint mindig, a probléma egy világos megfogalmazásával indulunk. Van jelöltünk (talán pályázók egy munkára, vagy lehetséges házassági partnerek). Feltevéseink:
Ezek a feltevések természetesen a valós alkalmazásokban teljesen elfogadhatók. Az utolsó feltevés például, hogy ismert, a titkárnő interpretációban helyénvalóbb, mint a házassági interpretációban.
Mi az optimális stratégia? Ezzel a stratégiával mekkora a ( legjobb ) választás valószínűsége? Mi történik a stratégiával, és a valószínűséggel, ha ? Speciálisan, nagy esetén,van remény a legjobb jelölt megtalálására?
Játsszuk le a titkárnő játékot néhányszor jelölttel. Nézze meg, hogy van-e különbség a teljesítményben!
A titkárnőjáték néhényszori lejátszása után, világos lesz, hogy a stratégiának csak az a típusa elfogadható, amikor bizonyos számú,
jelölt már elhaladt és ekkor kiválasztjuk az első jelöltet, aki jobb, mint az összes, eddigi jelölt (ha létezik ilyen). Ha nem létezik (azaz, ha nincs olyan jelölt, aki az összes eddigi jelöltnél jobb), akkor megállapodunk, hogy az utolsó jelöltet fogadjuk el, annak ellenére, hogy ez kudarcot jelent. A
paraméternek 1 és
között kell lennie; ha
, akkor válasszuk az 1. jelöltet; ha
, akkor válsszuk az utolsó jelöltet;
bármely más értéke esetén a jelöltet véletlenszerűen válasszuk ki, a
halmazból.
Erre az engedjünk el
jelöltet
módszerre, mint
stratégia-ként fogunk hivatkozni.
Így, nekünk ki kell számítanunk a valószínűséget stratégiát használva jelölt esetén. Ekkor maximalizálni tudjuk a feletti valószínűséget és meg tudjuk adni az optimális stratégiát, továbbá az szerinti határértéket és tanulmányozni tudjuk az aszimptotikát.
Először végezzük el az alapszámításokat.
Az esetre listázzuk ki az elemek permutációit és ellenőrizzük az alábbi táblában szereplő valószínűségeket. Megemlítjük, hogy az optimális.
| 1 | 2 | 3 | |
Játsszuk le a titkárnő játékot néhányszor jelöltre felhasználva a következő stratégiákat. Nézze meg, hogy van-e különbség a teljesítményben!
Az esetben listázza ki az elemek permutációit és ellenőrizze a valószínűségeket az alábbi táblázatban. Vegye észre, hogy az optimális.
| 1 | 2 | 3 | 4 | |
Játssza le a titkárnő játékot néhányszor jelölttel, felhasználva a következő startégiákat. Nézze meg, hogy van-e különbség a teljesítményben!
Az esetre listázza ki az elemek permutációit és ellenőrizze a valószínűségeket az alábbi táblázatban. Vegye észre, hogy az optimális.
| 1 | 2 | 3 | 4 | 5 | |
Játssza le a titkárnő játékot néhányszor jelöltre felhasználva a következő stratégiákat: lássa, ha különbséget észlel a véghezvitelben.
Nos, világos, hogy nem akarjuk folytatni ezt. Nézzük, mennyiben tudunk találni egy általános elemzést. jelölttel, jelölje a legjobb jelölt (érkezési sorrend szerint) számát, és jelölje a stratégia esetén a sikeres eseményt (azaz, hogy megtaláltuk a legjobb jelöltet).
Bizonyítsuk be, hogy mivel a jelöltek véletlenszerű sorrendben jönnek, egyenletes eloszlású a halmazon.
Bizonyítsuk be, hogy
A következőkben két esetet illusztrálunk. A nagy pont a legjobb jelöltet jelöli. A piros pontok azokat a jelölteket jelölik, akiket elutasítottunk, míg a kékek azokat, akiket megvizsgáltunk.


Felhasználva az előző gyakorlat eredményeit és egy feltételes érvelést, mutassuk meg, hogy
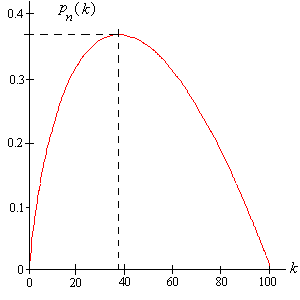
A függvény értékeit ki tudjuk könnyen számolni kis értékek esetén és számítógépes algebra rendszer segítségével közepesen nagy számok esetén. A ábrája látható a következő ábrán. Megjegyezzük, hogy a gráf alulról konkáv alakú és optimális értéke 38-nál van. Az optimális valószínűség 0.37104.
Az optimális stratégia -re, a hányados és a a legjobb jelölt megtalására vonatkozó optimális valószínűséget, mint függvényét a következő táblázatban adtuk meg:
| Jelöltek | Optimális stratégia | Hányados | Optimális valószínűség |
|---|---|---|---|
| 3 | 2 | 0.6667 | 0.5000 |
| 4 | 2 | 0.5000 | 0.4853 |
| 5 | 3 | 0.6000 | 0.4333 |
| 6 | 3 | 0.5000 | 0.4278 |
| 7 | 3 | 0.4286 | 0.4143 |
| 8 | 4 | 0.5000 | 0.4098 |
| 9 | 4 | 0.4444 | 0.4060 |
| 10 | 4 | 0.4000 | 0.3987 |
| 11 | 5 | 0.4545 | 0.3984 |
| 12 | 5 | 0.4167 | 0.3955 |
| 13 | 6 | 0.4615 | 0.3923 |
| 14 | 6 | 0.4286 | 0.3917 |
| 15 | 6 | 0.4000 | 0.3894 |
| 16 | 7 | 0.4375 | 0.3881 |
| 17 | 7 | 0.4118 | 0.3873 |
| 18 | 7 | 0.3889 | 0.3854 |
| 19 | 8 | 0.4211 | 0.3850 |
| 20 | 8 | 0.4000 | 0.3842 |
Kétségtelenül, mint várható volt, a optimális stratégia növekszik és a csökken, amint növekszik. Másrészt, az bíztató és egy kicsit meglepő, hogy az optimális valószínűség nem csökken 0-ig. Az talán legkevésbé világos, mi történik a hányadossal. A táblázatban néhány információ grafikus megjelenítése segíthet:
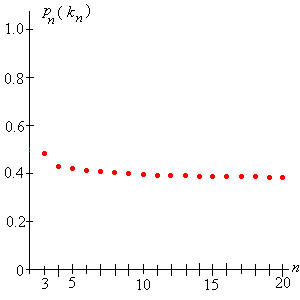 |
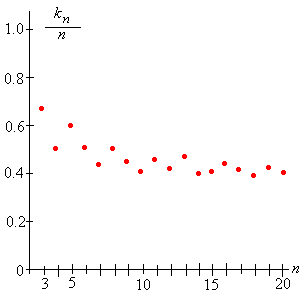 |
Segíthet-e, hogy a hányados és a valószínűség mindegyike konvergál és emellett ugyanahhoz az értékhez? Először próbáljunk kimutatni a táblázatban megfigyelt bizonyos trendeket.
Mutassuk meg, hogy
Adjunk valószínűségszámítási bizonyítást arra, hogy az optimális valószínűség csökken, ha növekszik.
Természetesen, minket érdekel a függvény aszimptotikus viselkedése és az optimális stratégia, ha . A kulcs annak felismerése, hogy egy egyszerű integrál Riemann összege. (A Riemann összegek természetesen Georg Riemann-ról kapta a nevét.)
Mutassuk meg, hogy
Az előző gyakorlatban lévő összegnek, mint balodali Riemann összegnek a felismerése az esetén a intervallum olyan részintervallumokra való bontása, melyek mindegyikének hossza :
Az előző két gyakorlatból következik, hogy
Még szigorúbban tételezzük fel, hogy -től függ és hogy ha . Így azon jelöltek határhányadosa, akiket azonnal elutasítunk.
Mutassuk meg, hogy ha .
A következő grafikon a valódi valószínűségeket mutatja és a határértékeket, mint függvényét esetén.
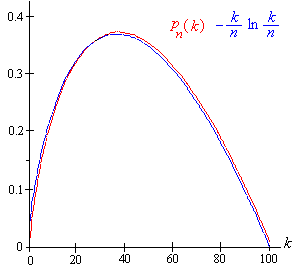
Könnyen maximalizálhatjuk a határfüggvényt.
Mutassuk meg, hogy maximuma értéknél van, és ez a maximum -vel egyenlő.
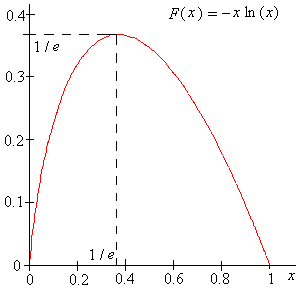
Így, az mágikus szám kétszer szerepel a problémában. Nagy esetén:
Tom Ferguson a probléma egy érdekes történeti diszkusszióját adja a "Who Solved the Secretary Problem? (magyarul: Ki oldotta meg a titkárnő problémát?)" c. cikkében, amely elmélkedést tartalmaz arról, hogy Johann Kepler lehetséges, hogy alkalmazta az optimális stratégiát második felesége kiválasztásánál. A cikk a probléma néhány általánosítását is elemzi.