10. laborgyakorlat

Numerikus számítások fizikusoknak

Kétváltozós függvények interpolációja
Kétváltozós függvények ábrázolása koordinátánként adott függvény esetén
Kétváltozós függvények ábrázolása képlettel adott függvény esetén
m-fájlok (szkriptek és függvények)
Beépített függvények
Hatvány-, logaritmus- és exponenciális függvények
Trigonometrikus és hiperbolikus függvények (sin, cos, tan, cot)
Számelmélet
Kerekítés
Adatfeldolgozás
Komplex számok
Numerikus deriválás és integrálás
Numerikus deriválás
Numerikus integrálás

clear all, close all

Kétváltozós függvények interpolációja

interp2 - lineáris interpoláció

x=[1,2,3,4]
y=[2,4,6]
Z=[7,15,22,30
   54,109,164,218
   403,807,1210,1614]
[X,Y]=meshgrid(x,y);
interp2(X,Y,Z,2.5,4.5)
%vagy
interp2(x,y,Z,2.5,4.5)

x =
     1     2     3     4
y =
     2     4     6
Z =
           7          15          22          30
          54         109         164         218
         403         807        1210        1614
ans =
    3.545000000000000e+002
ans =
    3.545000000000000e+002

Kétváltozós függvények ábrázolása koordinátánként adott függvény esetén

Az előző feladat adataival

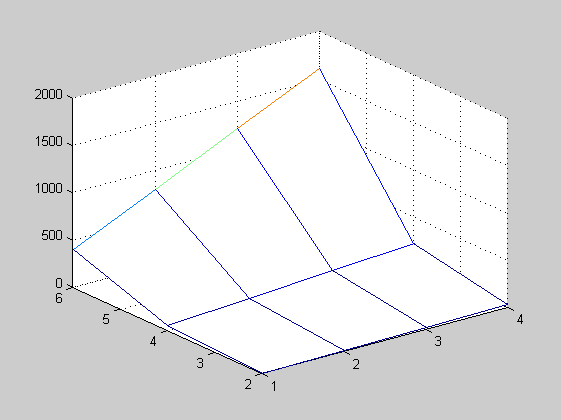
x=[1,2,3,4]
y=[2,4,6]
Z=[7,15,22,30
   54,109,164,218
   403,807,1210,1614]
[X,Y]=meshgrid(x,y)
mesh(X,Y,Z)

x =
     1     2     3     4
y =
     2     4     6
Z =
           7          15          22          30
          54         109         164         218
         403         807        1210        1614
X =
     1     2     3     4
     1     2     3     4
     1     2     3     4
Y =
     2     2     2     2
     4     4     4     4
     6     6     6     6

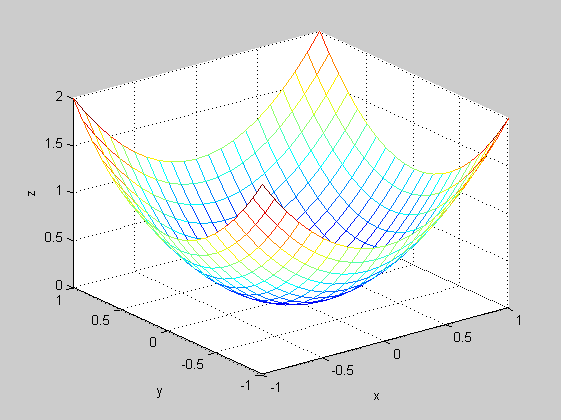
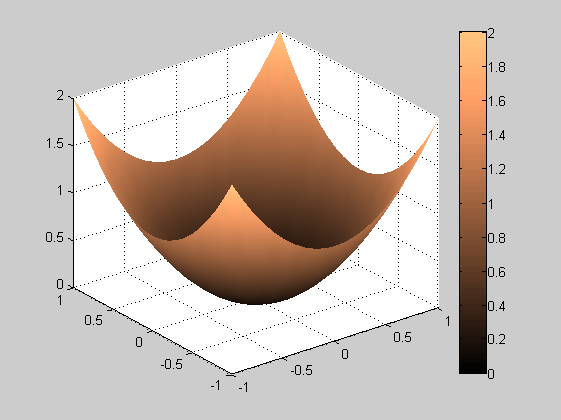
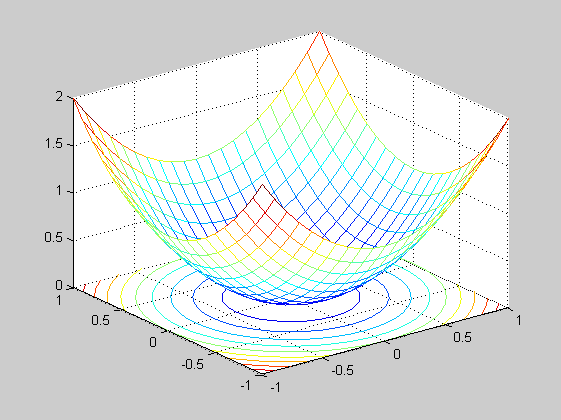
x=-1:0.1:1; y=-1:0.1:1;
[X,Y]=meshgrid(x,y);
Z=X.^2+Y.^2;
figure(1)
mesh(X,Y,Z)
xlabel('x')
ylabel('y')
zlabel('z')
pause
figure(2)
surf(X,Y,Z)
colorbar
colormap copper
shading interp

% colormap lehet pl: gray, hot, cool, bone, pink, flag, lsd. help.
% shading lehet pl: flat, interp, faceted, lsd. help
pause

figure(3)
meshc(X,Y,Z)
pause

figure(4)
contour(X,Y,Z)
pause
[c,h]=contour(X,Y,Z);
clabel(c,h)
pause
[c,h]=contour(X,Y,Z,0:0.1:1);
clabel(c,h)

Kétváltozós függvények ábrázolása képlettel adott függvény esetén

ezsurf, ezsurfc, ezmesh, ezmeshc, ezcontour

close all
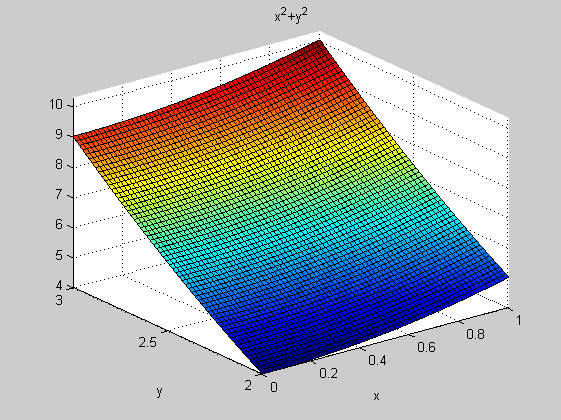
f=@(x,y)x.^2+y.^2

figure(1)
ezsurf(f,[0,1],[2,3])
pause
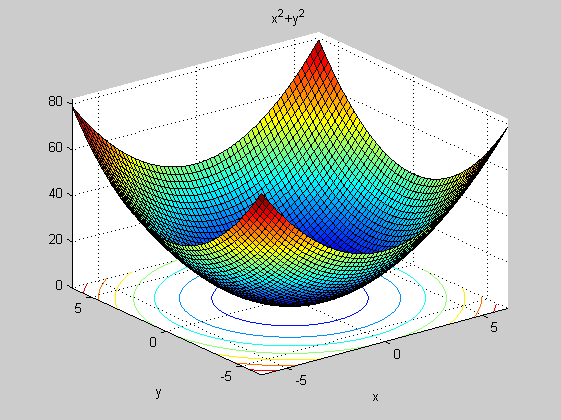
figure(2)
ezsurfc(f)
pause
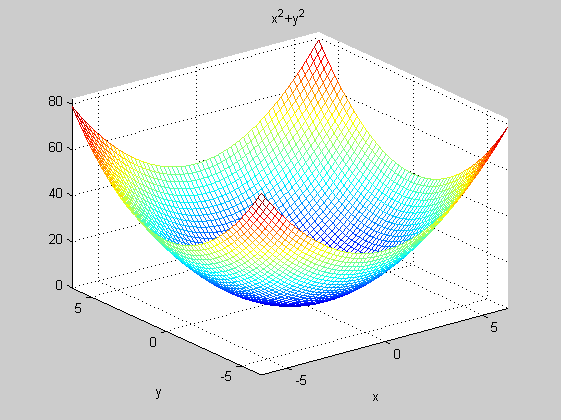
figure(3)
ezmesh(f)
pause
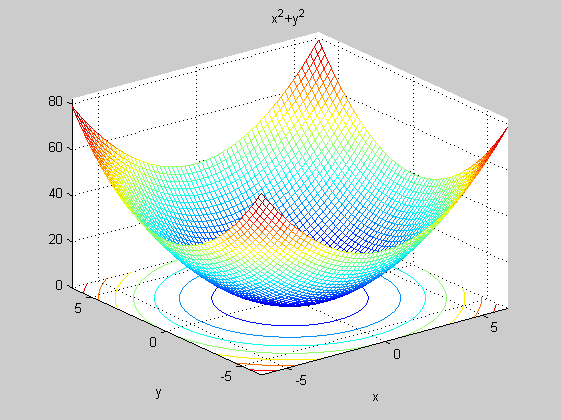
figure(4)
ezmeshc(f)
pause
figure(5)
ezcontour(f)

f = 
    @(x,y)x.^2+y.^2

m-fájlok (szkriptek és függvények)

A számológép üzemmód mellett parancsainkat elmenthetjük egy szövegfájlba is. Ezeket m-fájloknak hívjuk, mivel a Matlab *.m kiterjesztést ad nekik. Két fajtájuk van: szkriptek ill. függvények. A szkript egyszerűen csak egymás utáni parancsokat tartalmaz, és ha nev.m néven mentettük, akkor a parancssorba írt nev paranccsal futtatható. A szkript fájlban definiált változók a Workspace-en is megjelennek és viszont. A függvényeket tartalmazó m-fájlok a function [kimeneti változók]=függvénynév(bemeneti változók) sorral kezdődnek, és a készenléti jeltől a [kimeneti változók]=függvénynév(bemeneti változók) paranccsal futtathatók. A függvényekben definiált változók nem jelennek meg a Workspace-en és viszont.

Pl. egy függvényre: kerterfv.m

%{
  function [t,k]=mertek(a,b,c)
  % Használat: [k,t]=mertek(a,b,c). Három adat esetén a térfogatot és a
  % felszínt, két adat esetén a területet és a kerületet adja meg.
  if nargin == 2
    k=2*(a+b);
    t=a*b;
  else nargin == 3
    k=a*b*c;
    t=2*(a*c+a*b+b*c);
  end
%}

[kerulet,terulet]=mertek(3,4)
whos
help mertek

kerulet =
    12
terulet =
    14
  Name          Size             Bytes  Class              Attributes

  X            21x21              3528  double                       
  Y            21x21              3528  double                       
  Z            21x21              3528  double                       
  ans           1x1                  8  double                       
  c             2x594             9504  double                       
  f             1x1                 16  function_handle              
  h             1x1                  8  double                       
  kerulet       1x1                  8  double                       
  terulet       1x1                  8  double                       
  x             1x21               168  double                       
  y             1x21               168  double                       

  Használat: [k,t]=mertek(a,b,c). Három adat esetén a térfogatot és a 
  felszínt, két adat esetén a területet és a kerületet adja meg.

Beépített függvények

A Matlab tartalmaz számtalan előre telepített beépített függvényt. Ezek közül nézzük most át a legfontosabbakat. Bővebb információért mindig érdemes áttanulmányozni az adott paracs help oldalát! A Matlabhoz telepített különböző toolboxok is tulajdonképpen beépített Matlab függvények gyűjteményei.

Hatvány-, logaritmus- és exponenciális függvények

hatványozás

2^(1/2)

ans =
   1.414213562373095

négyzetgyök

sqrt(2)

ans =
   1.414213562373095

valós gyök

nthroot(-2,3) %

ans =
  -1.259921049894873

komplex gyök

(-2)^(1/3)

ans =
  0.629960524947437 + 1.091123635971721i

az e^x függvény

exp(1)

ans =
   2.718281828459046

e alapú logaritmus

log(5)

ans =
   1.609437912434100

10 alapú logaritmus

log10(10)

ans =
     1

2 alapú logaritmus

log2(4)

ans =
     2

Trigonometrikus és hiperbolikus függvények (sin, cos, tan, cot)

sin

sin(pi/2)

ans =
     1

arcsin

asin(1)

ans =
   1.570796326794897

sinh(1)

ans =
   1.175201193643801

arsh

asinh(2)

ans =
   1.443635475178810

Számelmélet

maradékos osztás maradéka

mod(16,3)

ans =
     1

Eldönti, hogy prím-e.

x=100:110;
[x;isprime(x)]'

Az összes prím 100-ig.

primes(100)

ans =
  Columns 1 through 13
     2     3     5     7    11    13    17    19    23    29    31    37    41
  Columns 14 through 25
    43    47    53    59    61    67    71    73    79    83    89    97

előjelfüggvény

sign([-10,0,2,10,-4])

ans =
    -1     0     1     1    -1

legnagyobb közös osztó

gcd(100,64)

ans =
     4

legkisebb közös többszörös

lcm(100,64)

ans =
        1600

prímfelbontás

factor(36)

ans =
     2     2     3     3

faktoriális

factorial(6)

ans =
   720

Kerekítés

x=[pi,-pi]

x =
   3.141592653589793  -3.141592653589793

kerekítés

round(x)

ans =
     3    -3

0 felé kerekítés

fix(x)

ans =
     3    -3

alsó egészrész

floor(x)

ans =
     3    -4

felső egészrész

ceil(x)

ans =
     4    -3

Adatfeldolgozás

x=[4,2,2,3], A=[1,5,3;4,2,6], B=[3,1,5;1,6,8]

x =
     4     2     2     3
A =
     1     5     3
     4     2     6
B =
     3     1     5
     1     6     8

x vektor minimális eleme (maximummal hasonlóan)

min(x)

ans =
     2

minimum értéke és hely

[m1,p1]=min(x)

oszloponkénti minimum

[m2,p2]=min(A)

m2 =
     1     2     3
p2 =
     1     2     1

minimummátrix

min(A,B)

ans =
     1     1     3
     1     2     6

átlag

mean(x)

ans =
   2.750000000000000

oszloponkénti átlag

mean(A)

ans =
   2.500000000000000   3.500000000000000   4.500000000000000

összeg

sum(x)

ans =
    11

oszloponkénti összeg

sum(A)

ans =
     5     7     9

szorzat

prod(x)

ans =
    48

oszloponkénti szorzat

prod(A)

ans =
     4    10    18

növekvő sorba rendezés

sort(x)

ans =
     2     2     3     4

csökkenő sorba rendezés

sort(x,'descend')

ans =
     4     3     2     2

első oszlop szerint rendezi a sorokat

sortrows(A)

ans =
     1     5     3
     4     2     6

3. oszlop szerint rendezi a sorokat

sortrows(A,3) % növekvő sorrend
sortrows(A,-3) % csökkenő sorrend

ans =
     1     5     3
     4     2     6
ans =
     4     2     6
     1     5     3

mátrix mérete

size(A)

ans =
     2     3

sorszám és oszlopszám maximuma

length(A)

ans =
     3

Komplex számok

i a képzetes egység

z=2+3*i

z =
  2.000000000000000 + 3.000000000000000i

komplex szám szöge

angle(z)

ans =
   0.982793723247329

abszolút érték

abs(z)

ans =
   3.605551275463989

valós rész

real(z)

ans =
     2

képzetes rész

imag(z)

ans =
     3

konjugált

conj(z)

ans =
  2.000000000000000 - 3.000000000000000i

További részletek a parancsok helpjében találhatók.

Numerikus deriválás és integrálás

Numerikus deriválás

Első derivált közelítése differenciahányadossal (elsőrendű)

f=@(x)x.^2;
fd=@(x)2*x;
fdd=@(x)2;
x=2;
fprintf('     h              derivált           hiba\n')
for i=1:10
    h=1/2^i;
deriv=(f(x+h)-f(x))/h;
fprintf('%10.8e    %10.8e    %10.8e\n',h,deriv,abs(deriv-fd(x)));
end

     h              derivált           hiba
5.00000000e-001    4.50000000e+000    5.00000000e-001
2.50000000e-001    4.25000000e+000    2.50000000e-001
1.25000000e-001    4.12500000e+000    1.25000000e-001
6.25000000e-002    4.06250000e+000    6.25000000e-002
3.12500000e-002    4.03125000e+000    3.12500000e-002
1.56250000e-002    4.01562500e+000    1.56250000e-002
7.81250000e-003    4.00781250e+000    7.81250000e-003
3.90625000e-003    4.00390625e+000    3.90625000e-003
1.95312500e-003    4.00195313e+000    1.95312500e-003
9.76562500e-004    4.00097656e+000    9.76562500e-004

Első derivált közelítése differenciahányadossal (másodrendű)

f=@(x)sin(x);
fd=@(x)cos(x);
fdd=@(x)-sin(x);
x=1;
fprintf('     h              derivált           hiba\n')
for i=1:10
    h=1/2^i;
deriv=(f(x+h)-f(x-h))/2/h;
fprintf('%10.8e    %10.8e    %10.8e\n',h,deriv,abs(deriv-fd(x)));
end

     h              derivált           hiba
5.00000000e-001    5.18069448e-001    2.22328579e-002
2.50000000e-001    5.34691719e-001    5.61058720e-003
1.25000000e-001    5.38896367e-001    1.40593842e-003
6.25000000e-002    5.39950615e-001    3.51690617e-004
3.12500000e-002    5.40214370e-001    8.79355346e-005
1.56250000e-002    5.40280321e-001    2.19846887e-005
7.81250000e-003    5.40296810e-001    5.49622251e-006
3.90625000e-003    5.40300932e-001    1.37405877e-006
1.95312500e-003    5.40301962e-001    3.43514885e-007
9.76562500e-004    5.40302220e-001    8.58787685e-008

Második derivált közelítése differenciahányadossal (másodrendű)

f=@(x)sin(x);
fd=@(x)cos(x);
fdd=@(x)-sin(x);
x=1;
fprintf('     h              derivált           hiba\n')
for i=1:10
    h=1/2^i;
deriv=(f(x-h)-2*f(x)+f(x+h))/h^2;
fprintf('%10.8e    %10.8e    %10.8e\n',h,deriv,abs(deriv-fdd(x)));
end

     h              derivált           hiba
5.00000000e-001    -8.24085778e-001    1.73852072e-002
2.50000000e-001    -8.37097444e-001    4.37354102e-003
1.25000000e-001    -8.40375890e-001    1.09509484e-003
6.25000000e-002    -8.41197104e-001    2.73880673e-004
3.12500000e-002    -8.41402508e-001    6.84768549e-005
1.56250000e-002    -8.41453865e-001    1.71196320e-005
7.81250000e-003    -8.41466705e-001    4.27993510e-006
3.90625000e-003    -8.41469915e-001    1.06998814e-006
1.95312500e-003    -8.41470717e-001    2.67500949e-007
9.76562500e-004    -8.41470918e-001    6.68882458e-008

Numerikus integrálás

quad parancs

quad(@sin,0,pi)
%vagy
f=@(x)sin(x);
quad(f,0,pi)

ans =
   1.999999996398431
ans =
   1.999999996398431