11. laborgyakorlat

Numerikus számítások fizikusoknak

Contents

clear all, close all

Numerikus integrálás

quad parancs

f=@(x)exp(-x.^2);
quad(f,0,2)
%vagy
quad('exp(-x.^2)',0,2)
%vagy az abszolút hiba megadásával
quad('exp(-x.^2)',0,2,10^-10)

ans =
   0.882081194911110
ans =
   0.882081194911110
ans =
   0.882081390750500

Trapézformula

f=@(x)exp(-x.^2);
n=111;
x=linspace(0,2,n);
y=f(x);

sum((diff(y)/2+y(1:n-1)).*diff(x))

% Egyforma osztásköz esetén
h=2/(n-1);
(y(1)/2+y(end)/2+sum(y(2:end-1)))*h

ans =
   0.882079372621402
ans =
   0.882079372621401

Simpson-formula

f=@(x)exp(-x.^2);
n=20;
x=linspace(0,2,2*n-1);
y=f(x);

% Egyforma osztásköz esetén
h=2/(n-1);
(y(1)+y(end)+4*sum(y(2:2:end-1))+2*sum(y(3:2:end-2)))*h/6

ans =
   0.882081359526869

Differenciálegyenletek megoldása

Kezdetiérték-feladatok

Euler-módszer

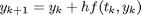
Runge-Kutta 4

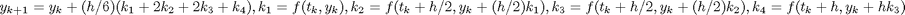
Euler-módszer

f=@(t,y)y;
t0=0;
y0=1;
tmax=1;
kmax=35;
h=(tmax-t0)/kmax;
t=t0;
yy(1)=y0;
for k=1:kmax
   yy(k+1)=yy(k)+h*f(t,yy(k));
   t=t+h;
end;
xxx=0:0.01:1;
yyy=exp(xxx);
tt=[t0:h:tmax];
plot(tt,yy,'o-',xxx,yyy,'r-')

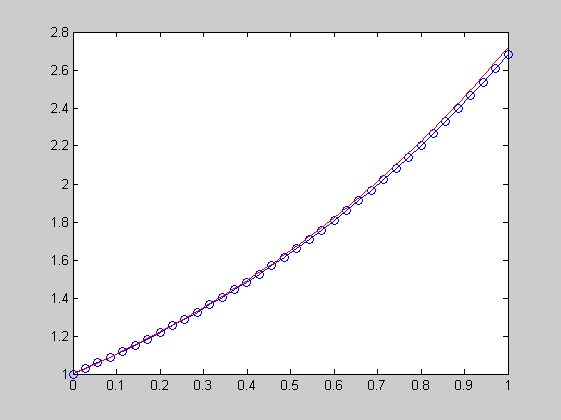
Negyedrendű Runge-Kutta-módszer

f=@(t,y)y;
t0=0;
y0=1;
tmax=1;
kmax=35;
h=(tmax-t0)/kmax;
t=t0;
yy(1)=y0;
for k=1:kmax
   k1=f(t,yy(k));
   k2=f(t+h/2,yy(k)+h*k1/2);
   k3=f(t+h/2,yy(k)+h*k2/2);
   k4=f(t+h,yy(k)+h*k3);
   yy(k+1)=yy(k)+h/6*(k1+2*k2+2*k3+k4);
   t=t+h;
end;
xxx=0:0.01:1;
yyy=exp(xxx);
tt=[t0:h:tmax];
plot(tt,yy,'o-',xxx,yyy,'r-')

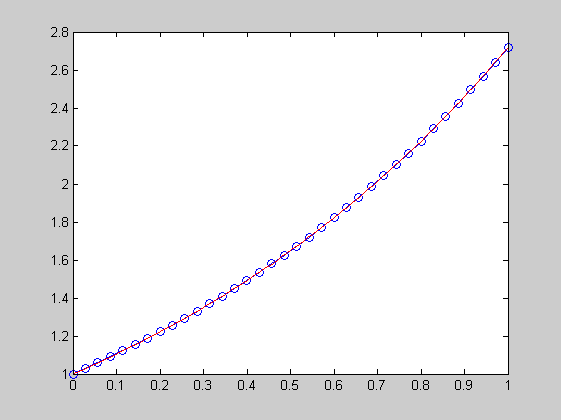
Megoldás a matlab beépített programjaival

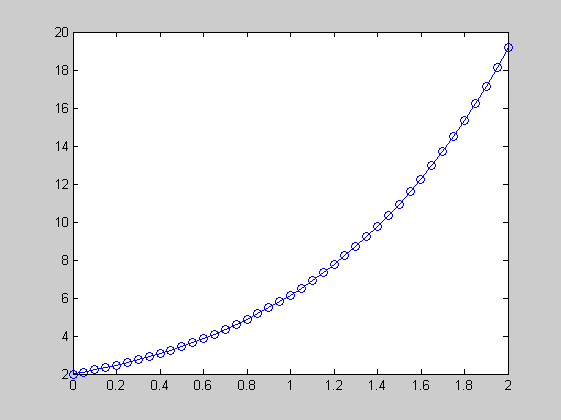
%(ode45, ode23, ode113, ode15s, ode23s, ode23t, ode23tb)
% Pl. ode45, [x,y]=ode45(f,tintervallum,y0), ha nem kérünk kimenő változót,
% akkor grafikont kapunk a megoldásról.

f=@(t,y)t+y; % f megadható Matlab függvényként is
ode45(f,[0,2],2)
[t,y]=ode45(f,[0,2],2)

t =
                   0
   0.050000000000000
   0.100000000000000
   0.150000000000000
   0.200000000000000
   0.250000000000000
   0.300000000000000
   0.350000000000000
   0.400000000000000
   0.450000000000000
   0.500000000000000
   0.550000000000000
   0.600000000000000
   0.650000000000000
   0.700000000000000
   0.750000000000000
   0.800000000000000
   0.850000000000000
   0.900000000000000
   0.950000000000000
   1.000000000000000
   1.050000000000000
   1.100000000000000
   1.150000000000000
   1.200000000000000
   1.250000000000000
   1.300000000000000
   1.350000000000000
   1.400000000000000
   1.450000000000000
   1.500000000000000
   1.550000000000000
   1.600000000000000
   1.650000000000000
   1.700000000000000
   1.750000000000000
   1.800000000000000
   1.850000000000000
   1.900000000000000
   1.950000000000000
   2.000000000000000
y =
   2.000000000000000
   2.103813590125000
   2.215513162000000
   2.335502904125000
   2.464208320000000
   2.602076665555032
   2.749576971089970
   2.907202913559662
   3.075474204119074
   3.254937122401535
   3.446164543316089
   3.649759445264519
   3.866356604892830
   4.096623249660188
   4.341259090569270
   4.601000607112278
   4.876623117245087
   5.168941574436766
   5.478810607646518
   5.807129754968619
   6.154845991904594
   6.522954704881698
   6.912499740080876
   7.324579795825191
   7.760351510618490
   8.221030652203556
   8.707892177200728
   9.222278038788858
   9.765600958444280
  10.339345878259765
  10.945070033787276
  11.584412490361139
  12.259098749910502
  12.970942524825713
  13.721845826928668
  14.513810615164397
  15.348944422374553
  16.229462521902729
  17.157688036263107
  18.136066163663244
  19.167171050560814

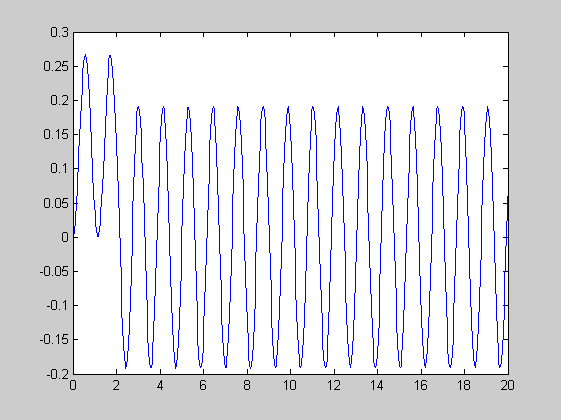
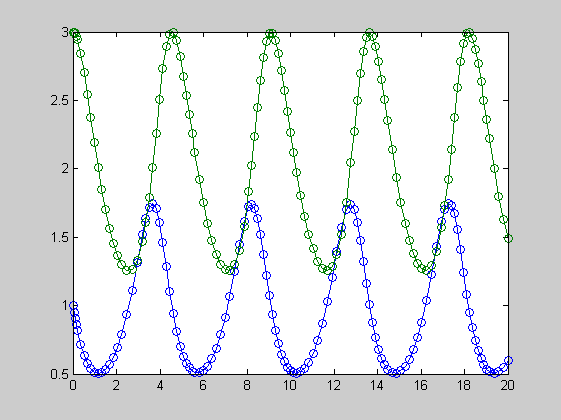
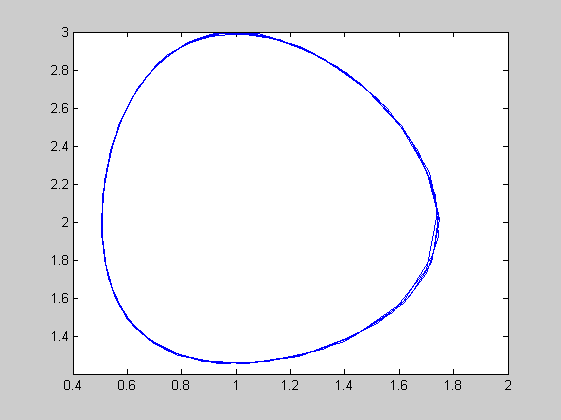
Differenciálegyenlet-rendszer

Példa

f=@(t,y)[y(1)*(2-y(2));y(2)*(y(1)-1)];
figure(1)
ode45(f,[0,20],[1,3])
[t,y]=ode45(f,[0,20],[1,3])
pause
figure(2)
plot(y(:,1),y(:,2))

t =
                   0
   0.050237728630192
   0.100475457260383
   0.150713185890575
   0.200950914520766
   0.354105716308268
   0.507260518095770
   0.660415319883272
   0.813570121670774
   0.985228093793834
   1.156886065916894
   1.328544038039954
   1.500202010163014
   1.686511985064330
   1.872821959965646
   2.059131934866962
   2.245441909768278
   2.480277584811522
   2.715113259854766
   2.949948934898011
   3.184784609941255
   3.342845191428611
   3.500905772915967
   3.658966354403324
   3.817026935890680
   3.975087517378036
   4.133148098865393
   4.291208680352749
   4.449269261840105
   4.607486189790270
   4.765703117740435
   4.923920045690600
   5.082136973640765
   5.212906079671490
   5.343675185702216
   5.474444291732941
   5.605213397763666
   5.798492547809351
   5.991771697855037
   6.185050847900723
   6.378329997946407
   6.585206261175618
   6.792082524404828
   6.998958787634038
   7.205835050863248
   7.425551521204222
   7.645267991545194
   7.864984461886166
   8.084700932227140
   8.219222464808299
   8.353743997389458
   8.488265529970617
   8.622787062551776
   8.757308595132935
   8.891830127714094
   9.026351660295253
   9.160873192876412
   9.302095723414293
   9.443318253952176
   9.584540784490059
   9.725763315027940
   9.866985845565822
  10.008208376103704
  10.149430906641587
  10.290653437179468
  10.476955347847667
  10.663257258515866
  10.849559169184063
  11.035861079852262
  11.257153174806737
  11.478445269761210
  11.699737364715684
...

Példa

f=@(t,y)[y(2);min(10*t,20)/2.5-75/2.5*y(1)];
[t,y]=ode45(f,[0,20],[0,0]);
plot(t,y(:,2))

Published with MATLAB® 7.6