3. laborgyakorlat

Numerikus számítások fizikusoknak

Contents

clear all, close all

Skaláris- és vektoriális szorzás

x=[1,2,3], y=[5,6,7]
dot(x,y) % skaláris szorzás
cross(x,y) % vektoriális szorzás

x =
     1     2     3
y =
     5     6     7
ans =
    38
ans =
    -4     8    -4

Lineáris egyenletrendszerek megoldása

Egyenletmegoldás

H=hilb(8) % Hilbert-mátrix, h_{ij}=1/(i+j-1)
b=ones(8,1)

x=linsolve(H,b) % lin. egyenletrendszer megoldása, vagy
x=H\b % balról osztás művelet

H =
  Columns 1 through 7
    1.0000    0.5000    0.3333    0.2500    0.2000    0.1667    0.1429
    0.5000    0.3333    0.2500    0.2000    0.1667    0.1429    0.1250
    0.3333    0.2500    0.2000    0.1667    0.1429    0.1250    0.1111
    0.2500    0.2000    0.1667    0.1429    0.1250    0.1111    0.1000
    0.2000    0.1667    0.1429    0.1250    0.1111    0.1000    0.0909
    0.1667    0.1429    0.1250    0.1111    0.1000    0.0909    0.0833
    0.1429    0.1250    0.1111    0.1000    0.0909    0.0833    0.0769
    0.1250    0.1111    0.1000    0.0909    0.0833    0.0769    0.0714
  Column 8
    0.1250
    0.1111
    0.1000
    0.0909
    0.0833
    0.0769
    0.0714
    0.0667
b =
     1
     1
     1
     1
     1
     1
     1
     1
x =
  1.0e+005 *
   -0.0001
    0.0050
   -0.0756
    0.4620
   -1.3860
    2.1622
   -1.6817
    0.5148
x =
  1.0e+005 *
   -0.0001
    0.0050
   -0.0756
    0.4620
   -1.3860
    2.1622
   -1.6817
    0.5148

Más példa balról ill. jobbról osztásra.

A=[1,2;3,4]; B=[3,5;2,4];
X=A\B % AX=B megoldása
A*X
X=B/A % XA=B megoldása
X*A

X =
   -4.0000   -6.0000
    3.5000    5.5000
ans =
     3     5
     2     4
X =
    1.5000    0.5000
    2.0000         0
ans =
     3     5
     2     4

A kondíciószám fogalma

Egy mátrix kondíciószáma azt méri, hogy az egyenletrendszer adatainak megváltozása mekkora hatással van az eredmény megváltozására (ha nagy, az a rossz). Parancsa: cond(A). A Hilbert-mátrix rosszul kondicionált. A lenti érték azt mutatja, hogy 1%-ot változtatva az adatokon, a megoldás akár 1.5*10^10 %-ot is változhat.

cond(H)

ans =
  1.5258e+010

b(end)=1.01
y=H\b;
megoldasbeli_kulonbseg=y-x
megoldasbeli_szazalekos_kulonbseg=(y-x)./x*100

b =
    1.0000
    1.0000
    1.0000
    1.0000
    1.0000
    1.0000
    1.0000
    1.0100
megoldasbeli_kulonbseg =
  1.0e+006 *
   -0.0005
    0.0288
   -0.3892
    2.1622
   -5.9459
    8.5622
   -6.1838
    1.7668
megoldasbeli_szazalekos_kulonbseg =
  1.0e+003 *
    6.4350
    5.7200
    5.1480
    4.6800
    4.2900
    3.9600
    3.6771
    3.4320

Vektorok távolsága

Vektorok távolsága maximum- ill. 2-es normában.

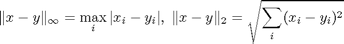
norm(megoldasbeli_kulonbseg,inf) % max. norma
norm(megoldasbeli_kulonbseg) % 2-es norma

ans =
  8.5622e+006
ans =
  1.2444e+007

LU-felbontás

Linenáris egyenletrendszerek általános megoldási módszere a Gauss-módszer. Ez egy eliminációs lépésből és egy visszahelyetesítési lépésből áll. A módszer végrehajtása folyamán létrejön egy L alsó háromszögmátrix 1-esekkel a főátlóban, és egy U felső háromszögmátrix. Ezen mátrixokkal az A mátrix A=LU alakban írható. (A konkrét megvalósítás, a műveletszámok összehasonlítása gyakorlaton.)

A futási idő mérése

A tic, toc, clock parancsok használata.

A=rand(1000); b=rand(1000,1);
tic, A\b; toc
tic, inv(A)*b; toc

Elapsed time is 0.493880 seconds.
Elapsed time is 0.917577 seconds.

Published with MATLAB® 7.6