4. laborgyakorlat

Numerikus számítások fizikusoknak

Gauss-módszer főelemkiválasztással
Általános LU-felbontás
Cholesky-felbontás
Teli- és ritka mátrixok
Futási idők összehasonlítása
Ciklusok
Egyszerű logikai műveletek
Iterációs egyenletrendszer-megoldás
Jacobi-iteráció

clear all, close all

Gauss-módszer főelemkiválasztással

A lebegőpontos számításokból eredő hibákat csökkenthetjük részleges- vagy teljes főelemkiválasztással. A részleges főelemkiválasztásnál sorcserét hajtunk végre úgy, hogy a főelem legyen a legnagyobb abszolút értékű elem az adott oszlop hátra lévő részében (A(k:n,k)-ban). Teljes főelemkiválasztásnál sor és oszlopot is cserélünk és az A(k:n,k:n+1) almátrixban lévő abszolút értékben legynagyobb elemet cseréljük a főelem helyére.

Általános LU-felbontás

A részleges főelemkiválasztással elvégzett Gauss-módszerrel egy

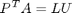
alakú ún. általános LU-felbontáshoz jutunk, ahol P megfelelő permutációs mátrix. L elemei most 1-nél nem nagyobb abszolút értékűek.

H=hilb(5)
[L,U,P]=lu(H) % Hilbert-mátrix általános LU-felbontása
P\(L*U) %=H

H =
    1.0000    0.5000    0.3333    0.2500    0.2000
    0.5000    0.3333    0.2500    0.2000    0.1667
    0.3333    0.2500    0.2000    0.1667    0.1429
    0.2500    0.2000    0.1667    0.1429    0.1250
    0.2000    0.1667    0.1429    0.1250    0.1111
L =
    1.0000         0         0         0         0
    0.3333    1.0000         0         0         0
    0.5000    1.0000    1.0000         0         0
    0.2000    0.8000   -0.9143    1.0000         0
    0.2500    0.9000   -0.6000    0.5000    1.0000
U =
    1.0000    0.5000    0.3333    0.2500    0.2000
         0    0.0833    0.0889    0.0833    0.0762
         0         0   -0.0056   -0.0083   -0.0095
         0         0         0    0.0007    0.0015
         0         0         0         0   -0.0000
P =
     1     0     0     0     0
     0     0     1     0     0
     0     1     0     0     0
     0     0     0     0     1
     0     0     0     1     0
ans =
    1.0000    0.5000    0.3333    0.2500    0.2000
    0.5000    0.3333    0.2500    0.2000    0.1667
    0.3333    0.2500    0.2000    0.1667    0.1429
    0.2500    0.2000    0.1667    0.1429    0.1250
    0.2000    0.1667    0.1429    0.1250    0.1111

Cholesky-felbontás

Cholesky-felbontás szimmetrikus, pozitív definit mátrixokra. Műveletszáma kb. fele a Gauss-módszerének

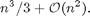
G=chol(H)
G'*G %=H

G =
    1.0000    0.5000    0.3333    0.2500    0.2000
         0    0.2887    0.2887    0.2598    0.2309
         0         0    0.0745    0.1118    0.1278
         0         0         0    0.0189    0.0378
         0         0         0         0    0.0048
ans =
    1.0000    0.5000    0.3333    0.2500    0.2000
    0.5000    0.3333    0.2500    0.2000    0.1667
    0.3333    0.2500    0.2000    0.1667    0.1429
    0.2500    0.2000    0.1667    0.1429    0.1250
    0.2000    0.1667    0.1429    0.1250    0.1111

Teli- és ritka mátrixok

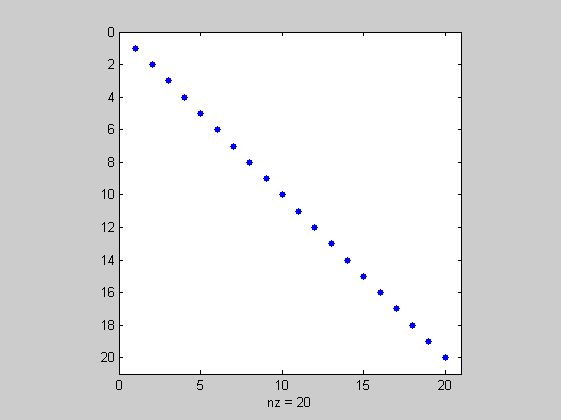
Egy mátrix ritka, ha a nemnulla elemek száma O(n) nagyságrendű. A sparse paranccsal lehet egy mátrixot ritkává (ekkor a Matlab tudja, hogy ritka mátrixról van szó) alakítani. A full parancs ritkából csinál teli mátrixot. spy ábrázolja a mátrix nemnulla elemeinek szerkezetét.

A=eye(20);
whos A
A=sparse(A);
whos A
spy(A)

  Name       Size            Bytes  Class     Attributes

  A         20x20             3200  double              

  Name       Size            Bytes  Class     Attributes

  A         20x20              324  double    sparse

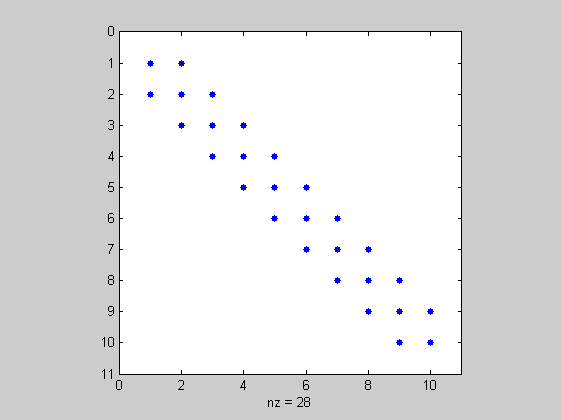
A=toeplitz([2,1,zeros(1,8)])
spy(A)

A =
     2     1     0     0     0     0     0     0     0     0
     1     2     1     0     0     0     0     0     0     0
     0     1     2     1     0     0     0     0     0     0
     0     0     1     2     1     0     0     0     0     0
     0     0     0     1     2     1     0     0     0     0
     0     0     0     0     1     2     1     0     0     0
     0     0     0     0     0     1     2     1     0     0
     0     0     0     0     0     0     1     2     1     0
     0     0     0     0     0     0     0     1     2     1
     0     0     0     0     0     0     0     0     1     2

Futási idők összehasonlítása

A=rand(1000); % véletlen mátrix
[L,U,P]=lu(A);
B=A'*A; % szimmetrikus, pozitív definit mátrix
C=toeplitz([2,-1,zeros(1,998)]); % tridiagonális mátrix
D=sparse(C);
b=rand(1000,1);

tic, A\b; altalanos_ido=toc
tic, U\(L\(P*b)); altalanos_LUval_ido=toc
tic, B\b; szimm_poz_def_ido=toc
tic, C\b; teli_tridiag_matrix_ido=toc
tic, D\b; ritka_tridiag_matrix_ido=toc

altalanos_ido =
    0.5663
altalanos_LUval_ido =
    0.0116
szimm_poz_def_ido =
    0.3485
teli_tridiag_matrix_ido =
    0.3140
ritka_tridiag_matrix_ido =
  2.4637e-004

Ciklusok

Azokat a programrészeket, melyeket a programmal ismételtetni szeretnénk ciklusoknak hívjuk. Kétféle ciklust használunk: for ill. while ciklust.

Példa for ciklusra

osszeg=0;
for i=1:2:999
    osszeg=osszeg+i^2;
end
osszeg

osszeg =
   166666500

Sokszor érdemes kiváltani vektor- ill. mátrixműveletekkel

sum([1:2:999].^2) % gyorsabb megvalósítás

ans =
   166666500

Példa while ciklusra

osszeg=0;
i=1;
while i<=999
    osszeg=osszeg+i^2;
    i=i+2;
end
osszeg

osszeg =
   166666500

Egyszerű logikai műveletek

1 az igaz, 0 a hamis logikai értéket jelenti

x=3; y=5;
x==y % egyenlő
x<y % kisebb
x>y % nagyobb
x<=y % kisebb vagy egyenlő
x>=y % nagyobb vagy egyenlő
x~=y % nem egyenlő

x>2 & x<4 % és
x>2 | y>6 % vagy
~(y==6) % tagadás

ans =
     0
ans =
     1
ans =
     0
ans =
     1
ans =
     0
ans =
     1
ans =
     1
ans =
     1
ans =
     1

Iterációs egyenletrendszer-megoldás

Egy vektoriteráció határértékeként állítjuk elő a megoldást

Jacobi-iteráció

A=[7,2,3;-1,6,4;1,4,8];
b=[2;5;7];
x_pontos=A\b % Ez a Matlab által adott megoldás

d=diag(A); % Az A diagonális elemeinek vektora.
B=A-diag(d); % Ugyanaz, mint A, csak a főátló helyén nullák állnak.

x=[1;2;3]; % Egy tetszőleges kezdővektor, ahonnét az iterációt indítjuk.

for i=1:25
   x=(b-B*x)./d
end