6. laborgyakorlat

Numerikus számítások fizikusoknak

Inline vagy anonim függvények létrehozása
Egyváltozós függvények ábrázolása
inline függvények ábrázolása
Koordinátánkénti ábrázolás
Több grafikon egy ábrában
Egyéb speciális grafikonok

clear all, close all

Inline vagy anonim függvények létrehozása

Ideiglenes jelleggel definiálhatunk a munkaterületen, ill. egy m-fájlon belül is függvényeket.

f=@(x,y)x^2-y^2 % kétváltozós függvény definiálása, f: függvény fogantyú
f(1,2)
whos f

f = 
    @(x,y)x^2-y^2
ans =
    -3
  Name      Size            Bytes  Class              Attributes

  f         1x1                16  function_handle

Használhatjuk a workspace változóit. A definiálás pillanatában rögzíti a Matlab ezeket a paramétereket.

a=3;
b=5;
f=@(x)a*x^2+b
f(1)
a=10;
f(1)

f = 
    @(x)a*x^2+b
ans =
     8
ans =
     8

Ahhoz, hogy vektorokra is használhassuk ezeket, a definícióban megfelelően kell definiálni őket.

f=@(x,y)x.^2-y.^2 % kétváltozós függvény definiálása
x=1:5, y=2:6
f(1,2)
f(x,y)

f = 
    @(x,y)x.^2-y.^2
x =
     1     2     3     4     5
y =
     2     3     4     5     6
ans =
    -3
ans =
    -3    -5    -7    -9   -11

Újabb példa - mátrix négyzetének determinánsa

negyzetdet=@(x)det(x^2)
negyzetdet([2,3;4,5])

negyzetdet = 
    @(x)det(x^2)
ans =
     4

Egyváltozós függvények ábrázolása

inline függvények ábrázolása

ezplot parancs. Alapból a [-2*pi,2*pi] intervallumon ábrázol, de megadható neki az intervallum is. Implicit függvények is ábrázolhatók vele.

f=@(x)x.^2
ezplot(f) % függvénynév, intervallum

f = 
    @(x)x.^2

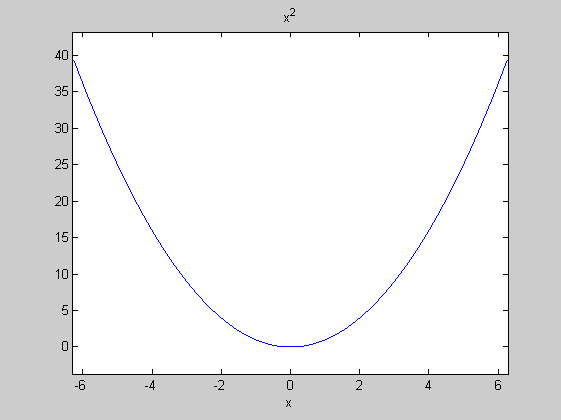
ezplot('x.^3',[-1,1]) % Karakterláncként is megadhatjuk a függvényt

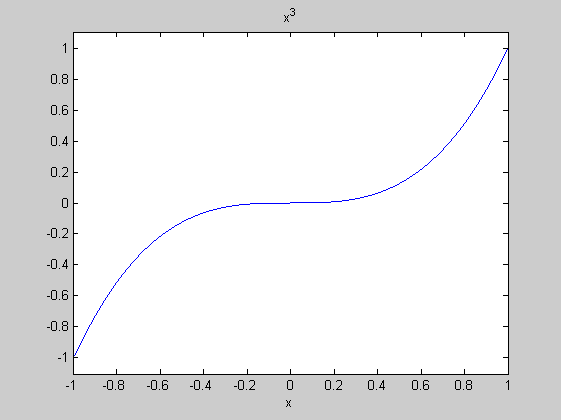
ezplot('x^2+y^2=1',[-2,2]) % Implicit függvény ábrázolása

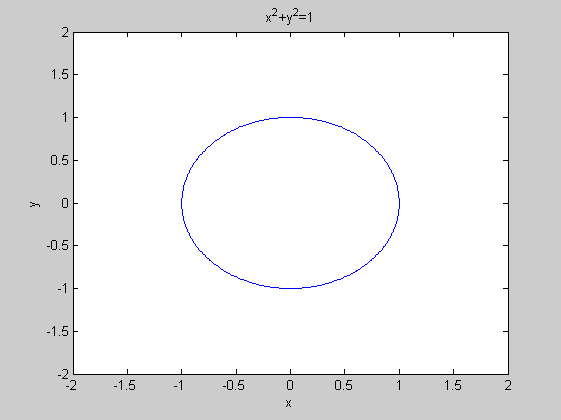
Koordinátánkénti ábrázolás

plot parancs. Az x- és y-koordináták vektorának segítségével való ábrázolás

x=linspace(-1,1,50);
y=x.^2;
plot(x,y)

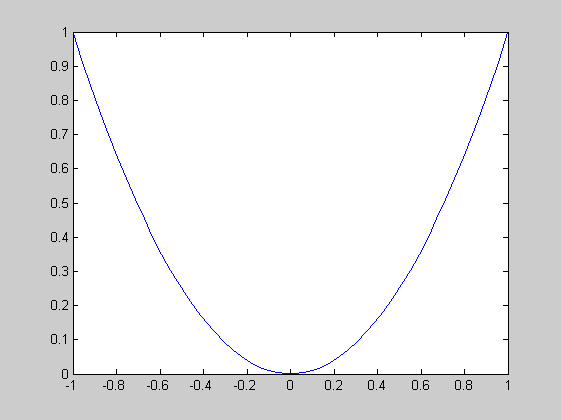
Az ábra csinosítása a plot parancs után megadott további parancsokkal történik.

x=linspace(-1,1,50);
y=x.^2;
plot(x,y,'r--*','LineWidth',2,'MarkerSize',8) % szín, vonaltípus, pontok szimbóluma, egyéb tulajd. (lásd a plot helpje).
title('Az x^2 függvény grafikonja. Aposztróf: '' ','FontSize',20)
xlabel('x-tengely','FontSize',20,'Color','red')
ylabel('y-tengely','FontSize',20,'Color','green')
legend('x^2')
axis([-1,1,0,2])
pause
axis equal % egyforma osztásköz a két tengelyen
grid on % rács bekapcsolása
pause
grid off % rács kikapcsolása

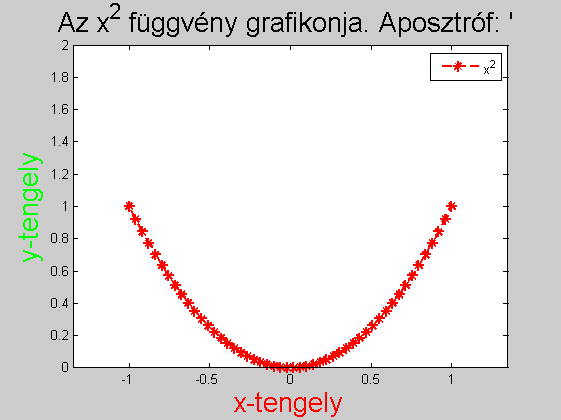
ezplot csinosítása*

h=ezplot('sin(x)')
set(h,'LineWidth',4) % Egyéb tulajdonságok a helpben.

h =
       4785.4

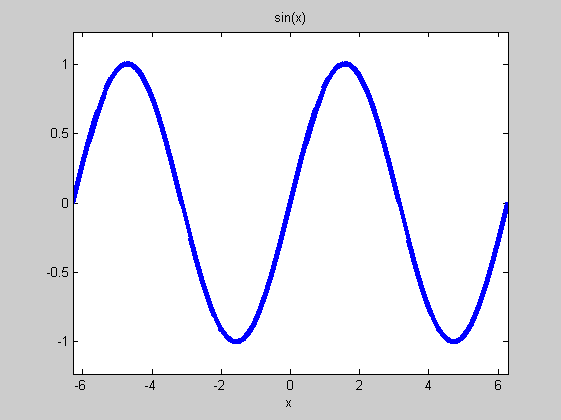
A grafikon menüből is csinosítható, de kilépés után a változtatások elvesznek. Vagy exportáljuk az ábrát vagy mentsük el fig fájlba!

Több grafikon egy ábrában

Egy plot parancsban több ábra

x=linspace(0,1,50);
y=sin(x); z=cos(x);
plot(x,y,'r-',x,z,'b--')

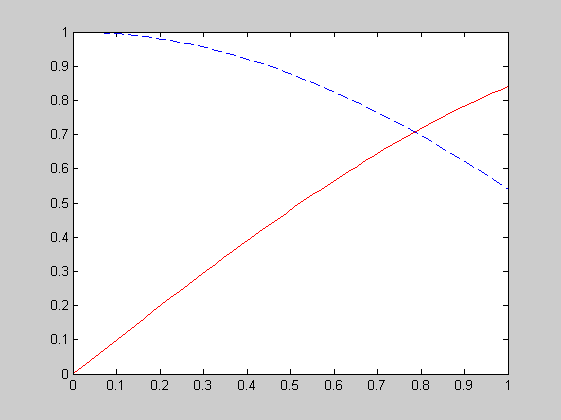
több grafikonablak

figure(1)
ezplot('sin(x)')
figure(2)
ezplot('cos(x)')
pause
figure(1)
h=ezplot('2*sin(x)');
set(h,'Linewidth',4)
pause
close 1
pause
close 2

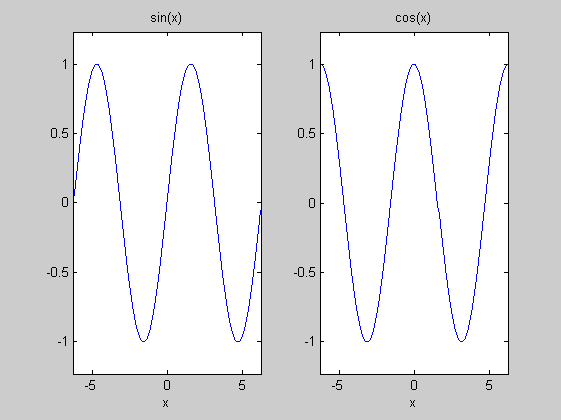
subplot - mátrixszerűen elrendezett ábrák

subplot(1,2,1)
ezplot('sin(x)')
subplot(1,2,2)
ezplot('cos(x)')

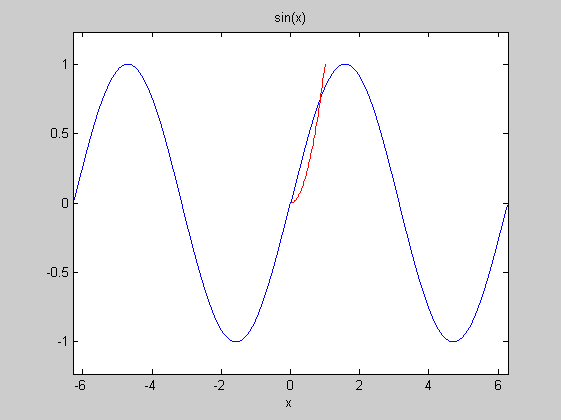
A hold parancs. Rögzíti a készült ábrát, és arra rajzolja rá a következőt.

close all
ezplot('sin(x)')
pause
hold on
x=linspace(0,1,50);
y=x.^2;
plot(x,y,'r-')
hold off

Egyéb speciális grafikonok

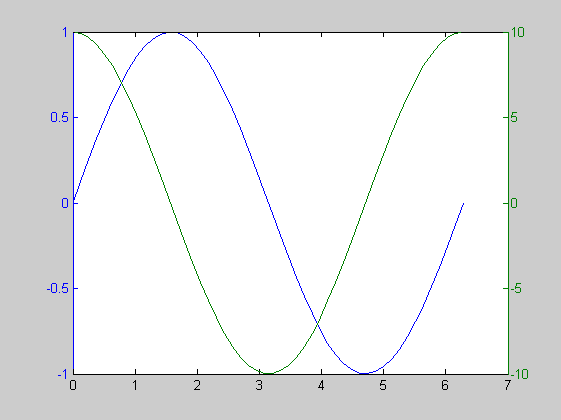
két y-tengely

x=linspace(0,2*pi,50);
y1=sin(x);
y2=10*cos(x);
plotyy(x,y1,x,y2)

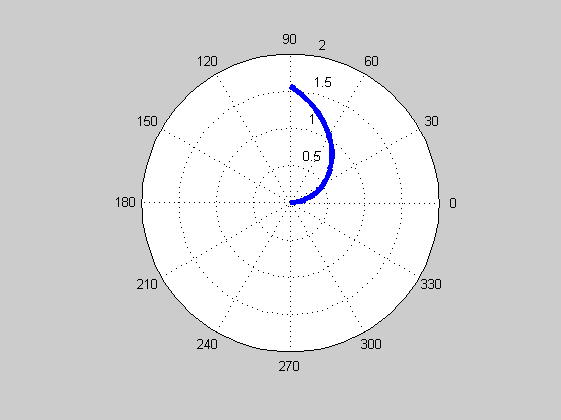
polár-koordináták

theta=linspace(0,pi/2,50);
r=ones(1,50);
h=polar(theta,r.*theta)
set(h,'LineWidth',4)

h =
       4812.4

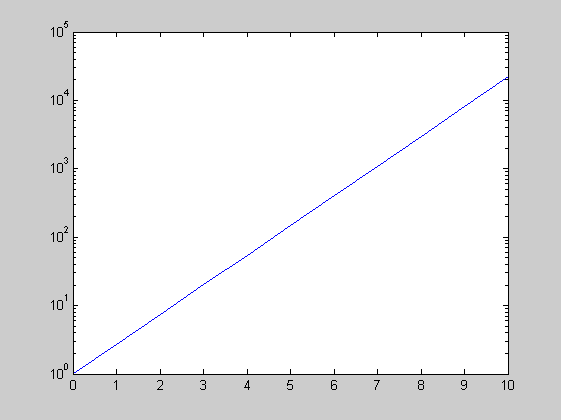
semilogy (semilogx hasonlóan)

x=0:10;
y=exp(x);
semilogy(x,y)

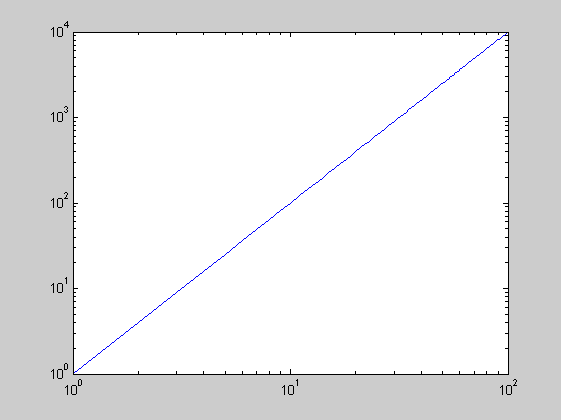
loglog

x=0:100;
y=x.^2;
loglog(x,y)

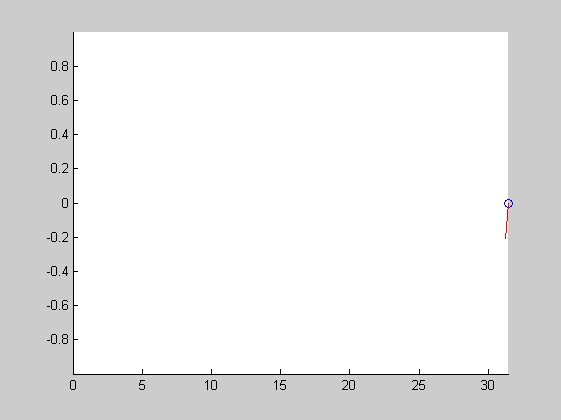
üstökös

x=linspace(0,10*pi,150);
y=sin(x);
comet(x,y)

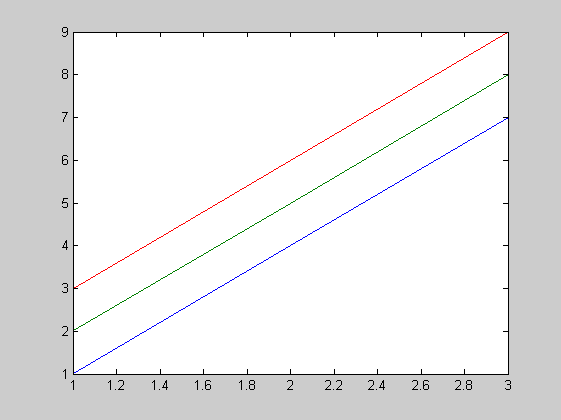
Mátrix ábrázolása, oszlopok sorindexek szerint

A=[1,2,3
   4,5,6
   7,8,9]

plot(A)

A =
     1     2     3
     4     5     6
     7     8     9

komplex elemű vektor ábrázolása a komplex számsíkon (mátrixnál csak a valós részt ábrázolja)

A=rand(5);
s=eig(A);
plot(s,'ro');